斩波调制∑-Δ ADC 噪声分析

杨建明

(安凯微电子技术有限公司，广州510663)

小信号模拟量测量要求数据转换器信噪比足够高，才可以识别微弱的模拟量。电路降噪成为设计关键。目前对电路噪声分析及多种降噪技术相继提出［1-2］。自动校零技术及与斩波调制技术是两种应用广泛的消除电路噪声技术。本文全面分析斩波调制∑-Δ ADC 噪声，旨在为小信号模拟量测量提供设计参考。

1 ∑-Δ ADC 噪声传递函数

分析∑-Δ ADC 噪声传递函数，找出影响∑-Δ ADC 精度的关键噪声。图1 所示为二阶∑-Δ ADC框图，其中Vni1、Vni2为积分器输入端噪声，Vno1、Vno2为积分器输出端噪声，e 为量化噪声。

推导噪声传递函数，

图1 二阶∑-Δ ADC

对各节点噪声传递函数做频谱分析，结果如图2 所示。

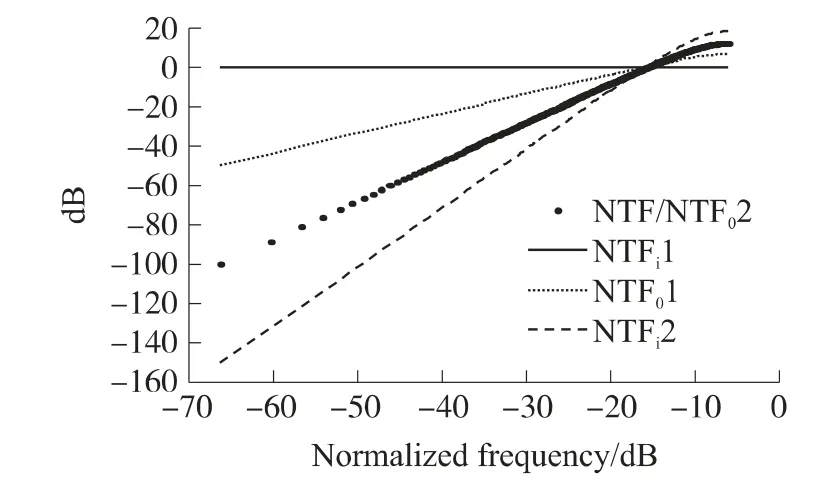
图2 噪声传递函数频谱

由图2 可见，第一阶积分器输入端噪声对∑-Δ ADC 精度影响最大。本文分析焦点为第一阶积分器输入端噪声。

2 斩波调制∑-Δ ADC 噪声源

∑-Δ ADC 通常基于开关电容电路实现，其核心模块开关电容积分器如图3 所示。

图3 开关电容积分器

2.1 采样开关噪声

开关器件导通对电容充电，无直流电流经过开关。故开关器件只产生热噪声(SS)，而不产生闪烁噪声。

开关器件热噪声被开关电路两相时钟交替采样保持。采样过程可以看作为单位脉冲串(图4(a))采样，保持过程可以看作为单位阶跃响应(图4(c))与单位脉冲串采样后的信号在时域卷积［3-4］。

开关热噪声双边功率谱密度SS=2kTRon。

图4 单位脉冲串与单位阶跃响应

2.1.1 PH1 期间开关热噪声

开关热噪声被采样并保持一个完整的时钟周期。该采样保持函数可以描述为:

vCS(t)为开关热噪声经过采样开关于采样电容形成的低通滤波器后，在采样电容端得到的热噪声电压。

推导频域内噪声功率谱密度传递函数。

其傅立叶变换为:

其傅立叶变换为:

采样后的开关热噪声变换到频域:

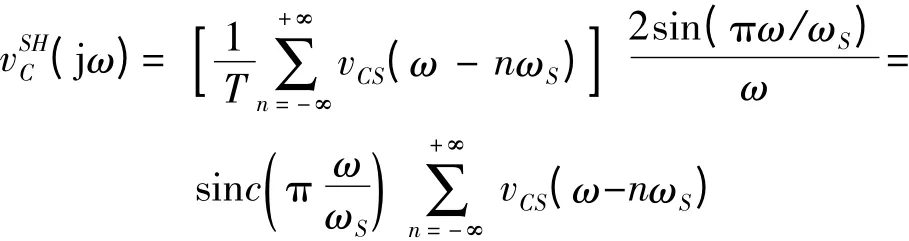
其对应的频域热噪声功率谱密度为:

定义:

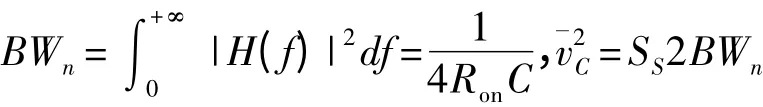
2.1.2 PH2 期间开关热噪声

热噪声被另外两个开关采样并保持一个完整的时钟周期。热噪声功率谱密度与PH1 期间近似相同:

2.2 OPAMP 1/f 噪声

1/f 噪声等效到输入信号端，相当于被斩波调制。斩波调制函数可以描述为:

其傅立叶变换:

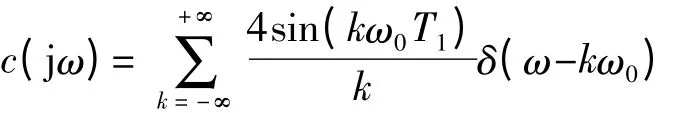
OP 1/f 噪声与斩波函数在时域相乘，对应频域卷积。

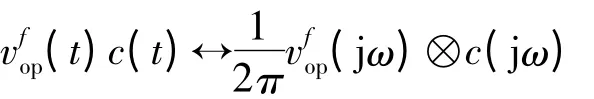
同理，OP 1/f 噪声功率谱密度函数经斩波调制后变为:

图5 为fch=fS/2 时1/f 噪声频谱图。由于OP有限带宽fc，折叠进入信号带内噪声为:

图5 斩波调制1/f 噪声频域响应

2.3 OPAMP 热噪声

由于热噪声为宽带噪声，斩波调制会使高频噪声折叠进入信号带内。

由于OP 有限带宽fc，OP 热噪声超过fc高频部分被抑制。斩波调制后，OP 热噪声功率谱密度有限项热噪声分量折叠进入信号带:

当fc/fch=6，斩波调制后，OP 等效输入热噪声为原来的90%。

图6 为fch=fS/2 时，斩波调制后热噪声前5 次分量及输入热噪声功率谱密度对比图。

图6 斩波调制热噪声频域响应

2.4 量化噪声

ADC 量化噪声为电路最强噪声源。可存在于DAC 反馈信号中，也寄生在电源/地中。通过恰当选择斩波频率，规避由于斩波调制折叠高频量化噪声进入信号带。

Early 选择斩波频率等于采样频率的一半，使斩波频率及其谐波落在ADC LPF 滤波器带外［7］。

Welland 认为选择斩波频率等于采样频率的一半实际上会调制更多的量化噪声进入信号带，故Welland 提出斩波频率应等于采样频率［8］。

上述两位作者分别从不同的侧面分析了斩波调制对量化噪声的影响。选择fch=fS/2，并不会把ADC 之DAC 反馈支路中所包含的量化噪声折叠进入信号带，如图7 所示。

图7 斩波调制量化噪声频域响应

但是对于电源/衬底中，寄生在fs/2 及其奇次谐波处的量化噪声，在斩波解调过程中，会直接折叠进入信号带。这就是很多芯片实测时，发现开启斩波调制/解调后，可以消除低频1/f 噪声，但白噪声平台被抬高。而Welland 提出的斩波频率等于采样频率结构，在斩波解调过程中，位于斩波调制频率及其奇次谐波处的量化噪声很低，故斩波解调不会折叠量化噪声进入信号带。

3 MATLAB 模型

本文通过电路仿真，提取出OPAMP 噪声数据后，导入MATLAB 分析ADC 噪声［9-10］。

3.1 MATLAB 模型

图8 为带斩波调制的二阶∑-Δ ADC 噪声模型，斩波频率为采样频率的一半。

图8 MATLAB 噪声模型

3.2 结果分析

图9所示为MATLAB 噪声模型仿真结果。曲线1 为理想二阶∑-Δ ADC 输出噪声频谱图;曲线3为包含开关热噪声、OPAMP 热噪声及1/f 噪声，未开启斩波调制下，输出信号噪声频谱图;曲线2 为开启斩波调制后的输出信号噪声频谱图。可见，斩波调制后，OPAMP 的低频1/f 噪声被抑制。表1 为三种情况下的仿真数据。

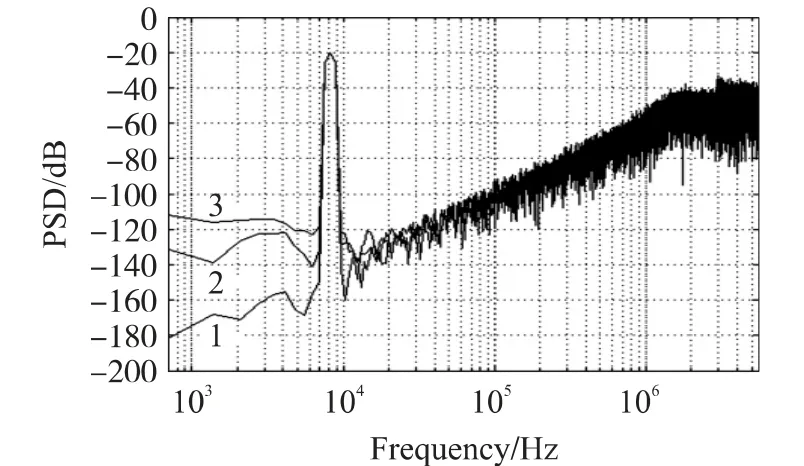
图9 仿真结果

表1 仿真数据 BW=22.05 kHz，OSR=256

4 结论

本文分析研究了斩波调制∑-Δ ADC 噪声传递函数，并建立MATLAB 数学模型，验证理论分析的可靠性。同时，实际设计中，要注意选取斩波调制频率与采样频率，避免寄生于电路节点的ADC 量化噪声由于斩波调制进入信号带。

［1］ Hsieh K C，Gray P R，Senderowicz D. A Low-Noise Chopper-Stabilized Differential Switched-Capacitor Filtering Technique［J］.IEEE Journal of Solid-State Circuits，1981，16(6):708-715.

［2］ Enz C C，Temes G C.Circuit Techniques for Reducing the Effects of Op-Amp Imperfections:Autozeroing，Correlated Double Sampling，and Chopper Stabilization［J］.Preceedings of the IEEE，1996，84(11):1584-1614.

［3］ Gobet C，Knob A. Noise Analysis of Switched Capacitor Networks［J］.IEEE Trans Circuits and Syst，1983，CAS-30(1):37-43.

［4］ Toth L，Yusim I，Suyama K. Noise Analysis of Ideal Switched-Capacitor Networks［J］. IEEE Trans Circuits and Syst，1999，46(3):349-363.

［5］ Oppenheim A V，Willsky A S，刘树棠. 信号与系统［M］. 西安:西安交通大学出版社，1998.

［6］ Gray P R，Hurst P J，Meyer R G. Analysis and Design of Analog Integrated Circuits［M］.John Wiley ＆ Sons，INC，2008.

［7］ US4939516 A B Early. Chopper Stabilized Delta-Sigma Analog to Digital Converter［P］.1990，7.

［8］ US5039989 D R Welland，Signore B P D，Kerth D A.Delta-Sigma Analog-to-Digital Converter with Chopper Stabilization at the Sampling Frequency［P］.1991.8.

［9］ Brigati S，Francesconi F，Malcovati P. Modeling Sigma-Delta Modulator Non-Ddealities in SIMULINK［J］.Proceedings of ISCAS 1999，2:384-387.

［10］ Francesconi A，Malcovati P，Malcovati F. Improved Modeling Sigma-Delta Modulator Non-Idealities in SIMULINK［J］. Proc of the IEEE International Symposium on Circuits and Systems，ISCAS 2005，Kobe 23-26(6):5982-5985.