古建筑木结构拼合梁结构机制
2013-12-21庆谭志成陈春超
淳 庆谭志成陈春超
(1东南大学城市与建筑遗产保护教育部重点实验室,南京 210096)
(2东南大学土木工程学院,南京 210096)
拼合是中国传统木作营造中梁栿制作的一种方法,是指以碎拼整或以简单形状拼复杂形状,从而达到以小料替代整材大木的目的.拼合梁历史悠久,在可考证的建筑实例中,从唐辽至明清,这一做法一直沿用不衰.在中国传统木构建筑中,拼合做法多见于梁架构件和檩条构件[1-2].
目前,国外学者对拼合木结构的研究主要针对胶合木结构[3-7],无论连接构造还是材质均与我国不同.而国内仅有少数学者对拼合木梁的受力性能进行了研究.周乾等[8]采用材料力学方法研究了古建筑木结构叠合梁和组合梁的弯曲受力问题.熊海贝等[9]通过试验研究了木基结构板-矩形截面木搁栅组合梁的抗弯性能.黄菊华等[10]讨论了不同叠合方式的叠合梁的应力分析问题, 得出不同材料、不同叠合方式对应力的影响规律.刘增夕等[11]和揭敏[12]分别研究了异性材料叠合梁和自由叠合梁的弯矩计算方法.综上所述,国内外学者并未对基于传统拼合做法的拼合梁结构机制进行研究.
1 拼合梁结构机制
1.1 三架梁模型
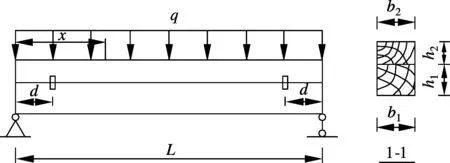
三架梁在跨度较大且受力较大时,往往通过在上部增设角背或在下部增设随梁枋的方法满足承载力和刚度的要求.图1为拼合三架梁模型.

图1 拼合三架梁模型
公式推导时采用下述简化和假设:① 拼合梁受弯后,上下梁截面应变分布符合平截面假定;② 木材材质均匀,无节疤、裂缝等天然缺陷,上下梁材质相同;③ 木材在拉、压、弯状态下的弹性模量相同;④ 木材在受拉时表现为线弹性,受压时表现为理想弹塑性;⑤ 上下梁之间完全靠销栓传递的剪力,忽略摩擦力;⑥ 销栓连接可靠,不存在滑移松动.
考虑荷载平衡方程和变形协调条件(即上梁下表面纤维与下梁上表面纤维在两连接点间的长度改变量相等),再考虑上下二梁的物理方程,就得到了补充方程,从而可求出销栓所受的剪力,即
(1)

(2)
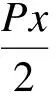
(3)

(4)
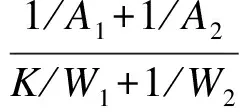


(5)
式中,P为跨中集中荷载;L为木梁跨度;d为销栓到支座的距离;h1为下梁截面高度;h2为上梁截面高度;A1为下梁截面面积;A2为上梁截面面积;W1为下梁截面抵抗矩;W2为上梁截面抵抗矩;K为下梁与上梁的惯性矩之比;b1为下梁宽度;b2为上梁宽度;E1为下梁弹性模量;E2为上梁弹性模量;N为销栓剪力;M1为下梁弯矩;M2为上梁弯矩.
拼合三架梁的破坏模式可分为2种:① 销栓首先破坏,形成叠合梁,随着荷载的增大,木梁最终破坏;② 销栓的强度很高,木梁率先达到极限强度而破坏.
1.1.1 破坏模式1
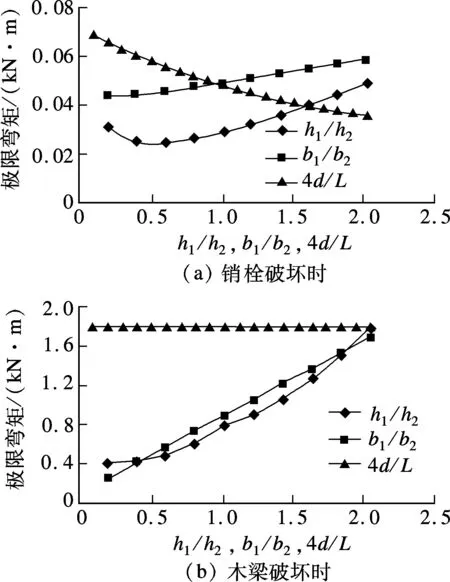
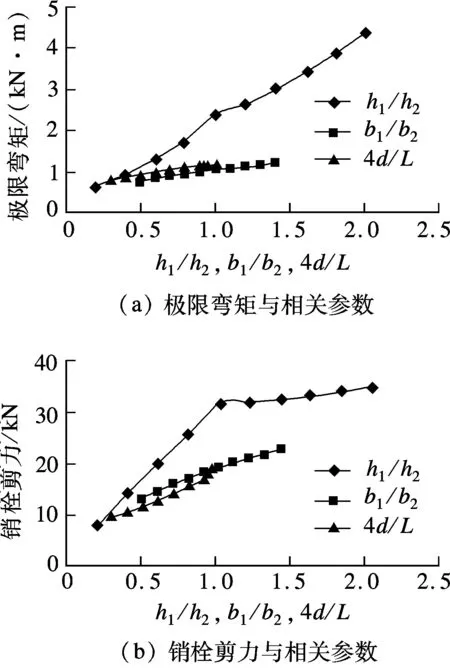
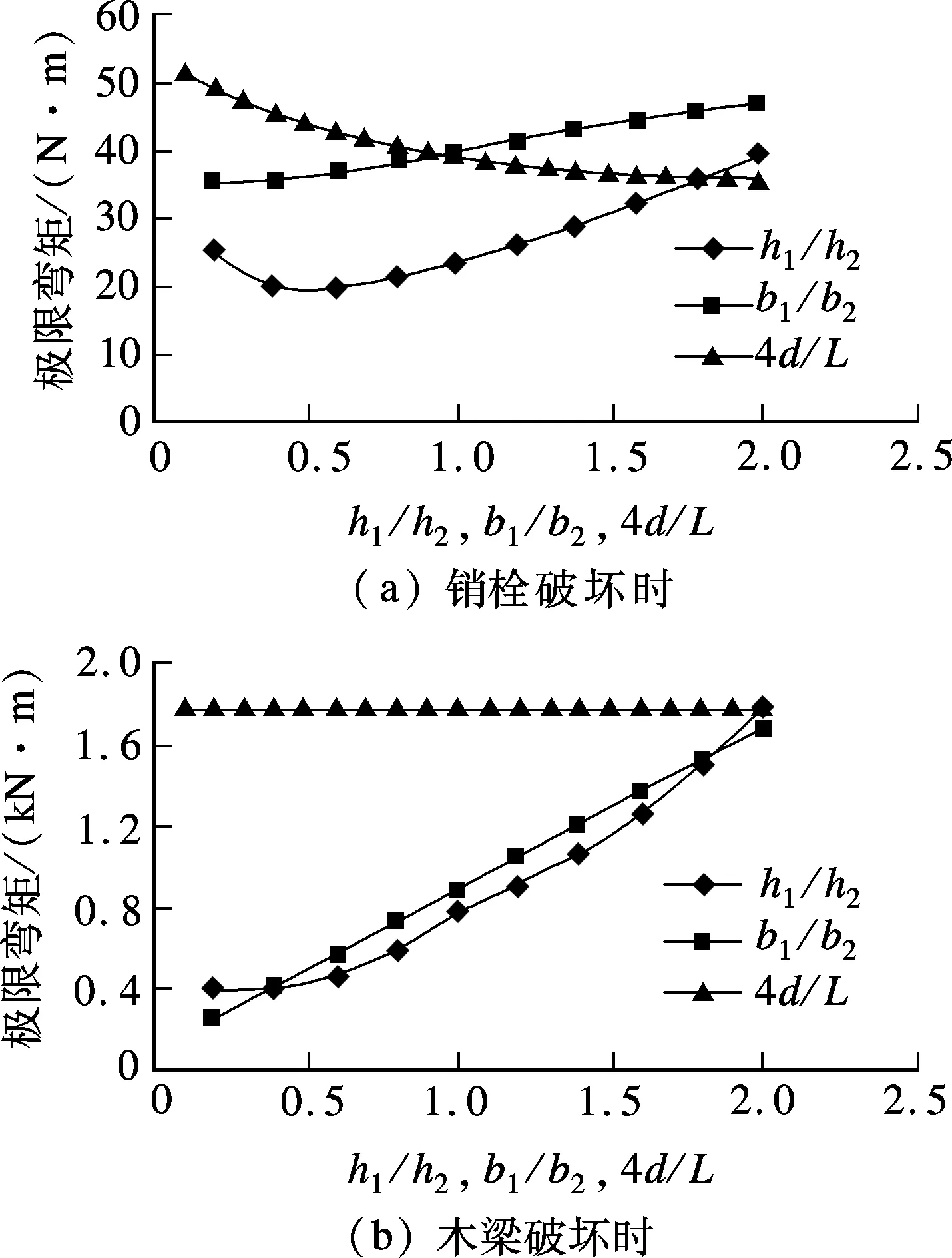
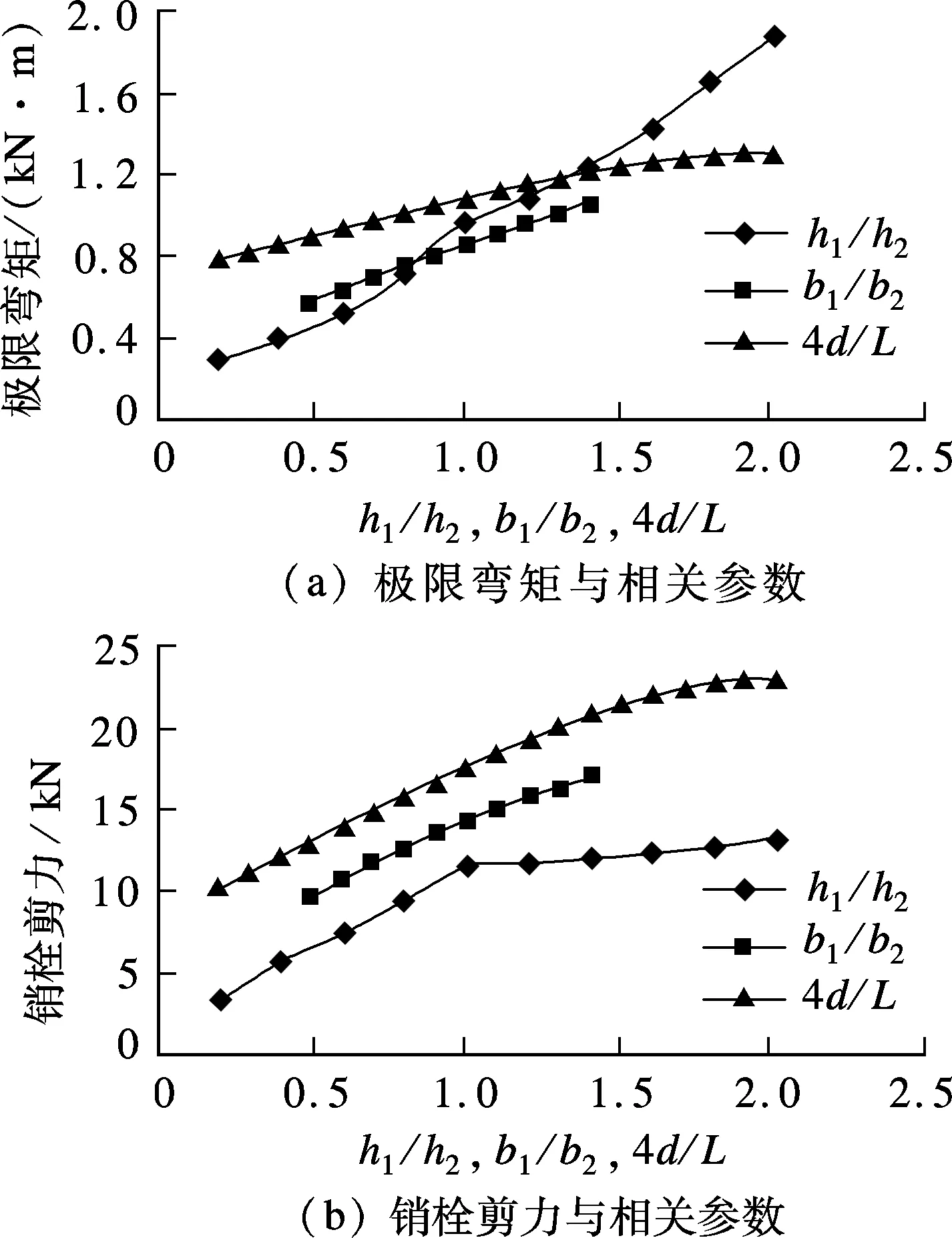
销栓破坏时,上下梁的极限弯矩需满足M1 (6) 式中,fv为木材顺纹抗剪强度.在销栓破坏后,形成叠合梁构件,在小变形情况下,两梁的曲率相同,则木梁最终破坏时的最大弯矩为 当h1>h2时 (7) 当h1≤h2时 (8) 破坏模式1下的极限弯矩与相关参数之间关系的比较如图2所示. 图2 三架梁极限弯矩与相关参数关系 从图2(a)可看出,随着h1/h2的增大,销栓破坏时的极限弯矩先减小后增大,当h1/h2接近0.5时,极限弯矩达到最小值,后随着h1/h2的增大而增大;随着b1/b2的增大,极限弯矩也逐渐变大,但幅度不大;随着4d/L的增大,销栓破坏时的极限弯矩迅速减少.经比较,销栓破坏时极限弯矩受4d/L的影响较大,h1/h2次之,b1/b2的影响较小.从图2(b)可看出,随着h1/h2的增大,木梁破坏时的极限弯矩也逐渐增大;随着b1/b2的增大,木梁破坏时的极限弯矩基本呈线性增大;木梁破坏时的极限弯矩与4d/L的比值无关.经比较,木梁破坏时的极限弯矩受h1/h2和b1/b2的影响相差不大. 1.1.2 破坏模式2 木梁破坏时的销栓剪力应满足N<2fvA/3,则木梁破坏时的最大弯矩为 当h1>h2(下梁先破坏)时 (9) 当h1≤h2(上梁先破坏)时 (10) 破坏模式2下的极限弯矩和销栓剪力与相关参数之间的关系如图3所示. 从图3(a)可看出,随着h1/h2的增大,木梁破坏时的极限弯矩迅速增大;随着b1/b2或4d/L的增大,木梁破坏时的极限弯矩慢慢增大.经比较,木梁破坏时的极限弯矩受h1/h2的影响较大,受b1/b2和4d/L的影响较小.从图3(b)可看出,随着h1/h2或b1/b2的增大,木梁破坏时的销栓剪力慢慢变大;随着4d/L的增大,木梁破坏时的销栓剪力迅速增大.经比较,4d/L对木梁破坏时的销栓剪力影响较大,h1/h2和b1/b2的影响较小. 图3 三架梁极限弯矩和销栓剪力与相关参数关系 五架梁在跨度较大且受力较大时,往往通过在上部增设角背或在下部增设随梁枋的方法满足承载力和刚度的要求.图4为拼合五架梁模型. 图4 拼合五架梁模型 与拼合三架梁类似,同样考虑荷载平衡方程及变形协调条件,再考虑上下二梁的物理方程,可求出销栓所受的剪力为 (11) 拼合五架梁的破坏模式同样可分为2种:① 销栓首先破坏,形成叠合梁,随着荷载的增大,木梁最终破坏;② 销栓的强度很高,木梁率先达到极限强度而破坏. 1.2.1 破坏模式1 销栓破坏时,上下梁的极限弯矩需满足M1 (12) 在销栓破坏后,形成叠合梁构件,在小变形情况下,两梁的曲率相同,则木梁最终破坏时的最大弯矩为 当h1>h2时, (13) 当h1≤h2时, (14) 破坏模式1下的极限弯矩与相关参数之间的关系如图5所示. 图5 五架梁极限弯矩与相关参数关系 从图5(a)可看出,随着h1/h2的增大,销栓破坏时的极限弯矩先减小后增大,当h1/h2接近0.5时,极限弯矩达到最小值,以后随着h1/h2的增大而增大;随着b1/b2的增大,销栓破坏时的极限弯矩也逐渐变大,但幅度不大;随着4d/L的增大,销栓破坏时的极限弯矩迅速减少.经比较,销栓破坏时的极限弯矩受4d/L的影响较大,h1/h2次之,b1/b2的影响较小.从图5(b)可看出,随着h1/h2的增大,木梁破坏时的极限弯矩也逐渐增大;随着b1/b2的增大,木梁破坏时的极限弯矩基本呈线性增大;木梁破坏时的极限弯矩与4d/L的比值无关.经比较,木梁破坏时的极限弯矩受h1/h2和b1/b2的影响相差不大. 1.2.2 破坏模式2 木梁破坏时的销栓剪力应满足N<2fvA/3,因此木梁破坏时的最大弯矩为 当h1>h2(下梁先破坏)时 (15) 当h1≤h2(上梁先破坏)时 (16) 破坏模式2下的极限弯矩和销栓剪力与相关参数之间的关系如图6所示. 图6 五架梁极限弯矩和销栓剪力与相关参数关系 从图6(a)可看出,随着h1/h2的增大,木梁破坏时的极限弯矩迅速增大;随着b1/b2或4d/L的增大,木梁破坏时的极限弯矩缓慢增大.经比较,木梁破坏时的极限弯矩受h1/h2的影响较大,受b1/b2和4d/L的影响较小.从图6(b)可看出,随着h1/h2的增大,木梁破坏时的销栓剪力迅速变大,后增幅减缓;随着b1/b2或4d/L的增大,木梁破坏时的销栓剪力也变大.经比较,当h1/h2<1时,h1/h2对木梁破坏时的销栓剪力影响较大,b1/b2和4d/L的影响较小;当h1/h2>1时,b1/b2和4d/L对木梁破坏时的销栓剪力影响较大,而h1/h2的影响较小. 檩条在跨度较大且受力较大时,往往通过在下部增设随檩枋的方法满足承载力和刚度的要求.图7为拼合檩条模型. 图7 拼合檩条模型 同样考虑荷载平衡方程及变形协调条件,再考虑上下二梁的物理方程,可求出销栓所受的剪力为 (17) 式中,q为檩条所受均布荷载.拼合檩条的破坏模式同样可分为2种:① 销栓首先破坏,形成叠合梁,随着荷载的增大,木梁最终破坏;② 销栓的强度很高,木梁率先达到极限强度而破坏. 销栓破坏时,上下梁的极限弯矩需满足M1 (18) 在销栓破坏后,形成叠合梁构件,在小变形情况下,两梁的曲率相同,则木梁最终破坏时的最大弯矩为 当h1>h2时 (19) 当h1≤h2时 (20) 破坏模式1下的极限弯矩与相关参数之间关系的比较如图8所示. 图8 拼合檩条结构极限弯矩与相关参数关系 从图8(a)可看出,随着h1/h2的增大,销栓破坏时的极限弯矩先减小后增大,当h1/h2接近0.5时,极限弯矩达到最小值,后随着h1/h2的增大而增大;随着b1/b2的增大,销栓破坏时的极限弯矩也逐渐变大,但幅度不大;随着4d/L的增大,销栓破坏时的极限弯矩迅速减少.经比较,销栓破坏时极限弯矩受4d/L的影响较大,h1/h2次之,b1/b2的影响较小.从图8(b)可看出,随着h1/h2的增大,木梁破坏时的极限弯矩也逐渐增大;随着b1/b2的增大,木梁破坏时的极限弯矩基本呈线性增大;木梁破坏时的极限弯矩与4d/L的比值无关.经比较,木梁破坏时的极限弯矩受h1/h2和b1/b2的影响相差不大. 木梁破坏时的销栓剪力应满足N<2fvA/3,因此木梁破坏时的最大弯矩为 当h1>h2(下梁先破坏)时, (21) 当h1≤h2(上梁先破坏)时, (22) 破坏模式2下的极限弯矩和销栓剪力与相关参数之间关系的比较如图9所示. 从图9(a)可看出,随着h1/h2的增大,木梁破坏时的极限弯矩迅速增大;随着b1/b2或4d/L的增大,木梁破坏时的极限弯矩缓慢增大.经比较,木梁破坏时的极限弯矩受h1/h2的影响较大,受b1/b2和4d/L的影响相对较小.从图9(b)可看出,随着h1/h2的增大,木梁破坏时的销栓剪力迅速变大,后增幅减缓;随着b1/b2的增大,木梁破坏时的销栓剪力也变大;随着4d/L的增大,木梁破坏时的销栓剪力迅速增大.经比较,总体而言,4d/L的变化对木梁破坏时的销栓剪力影响较大,b1/b2和h1/h2的影响相对较小. 图9 拼合檩条结构极限弯矩和销栓剪力与相关参数关系 1) 根据本文公式,可以对拼合三架梁模型、拼合五架梁模型及拼合檩条模型在不同破坏模式(销栓先破坏或木梁先破坏)下相应的极限荷载进行计算. 2) 对于拼合三架梁和拼合檩条而言,销栓先破坏时,销栓破坏时的极限弯矩受4d/L的影响最大,h1/h2次之,b1/b2的影响最小.木梁破坏时的极限弯矩与4d/L无关,受h1/h2和b1/b2的影响相差不大.木梁先破坏时,极限弯矩受h1/h2的影响较大,受b1/b2和4d/L的影响较小.销栓剪力受4d/L的影响较大,受h1/h2和b1/b2的影响较小. 3) 对于拼合五架梁而言,销栓先破坏时,销栓破坏时的极限弯矩受4d/L的影响最大,h1/h2次之,b1/b2的影响最小.木梁破坏时的极限弯矩与4d/L无关,受h1/h2和b1/b2的影响相差不大.木梁先破坏时,极限弯矩受h1/h2的影响较大,受b1/b2和4d/L的影响较小.当h1/h2<1时,销栓剪力受h1/h2的影响较大,受b1/b2和4d/L的影响较小;当h1/h2>1时,销栓剪力受b1/b2和4d/L的影响较大,受h1/h2的影响较小. ) [1]潘谷西, 何建中.《营造法式》解读[M]. 南京:东南大学出版社,2005. [2]张至刚, 刘敦桢.营造法原[M]. 北京:中国建筑工业出版社,1986. [3]Milner M W, Bainbridge R J. New opportunities for timber engineering [J].TheStructuralEngineer, 1997,75(16): 278-282. [4]Issa C A, Kmeid Z. Advanced wood engineering: glulam beams [J].ConstructionandBuildingMaterials, 2005,19(2): 99-106. [5]Serrano E, Gustafsson P J, Larsen H J. Modeling of finger-joint failure in glued-laminated timber beams [J].JournalofStructuralEngineering,ASCE, 2001,127(8): 914-921. [6]Castro G, Paganini F. Mixed glued laminated timber of poplar and Eucalyptus grandis clones [J].EuropeanJournalofWoodandWoodProducts, 2003,61(4):291-298. [7]Anshari B, Guan Z W, Kitamori A, et al. Structural behaviour of glued laminated timber beams pre-stressed by compressed wood [J].ConstructionandBuildingMaterials, 2012,29(4): 24-32. [8]周乾, 闫维明. 古建筑木结构叠合梁与组合梁弯曲受力研究[J]. 建筑结构, 2012,42(4): 157-161. Zhou Qian, Yan Weiming. Bending analysis on composite beam and combination beam of Chinese ancient wooden buildings [J].BuildingStructure, 2012,42(4): 157-161. (in Chinese) [9]熊海贝, 康加华,吕西林.木质组合梁抗弯性能试验研究[J].同济大学学报:自然科学版, 2012,40(4): 522-528. Xiong Haibei, Kang Jiahua, Lü Xilin. Bending tests investigation on composite timber beam[J].JournalofTongjiUniversity:NaturalScienceEdition, 2012,40(4): 522-528. (in Chinese) [10]黄菊华, 钱应平, 李厚民. 不同形式叠合梁的应力分析[J]. 湖北工业大学学报, 2008,23(3): 87-89. Huang Juhua, Qian Yingping, Li Houmin. Stress analysis of superposition beam of different forms[J].JournalofHubeiUniversityofTechnology, 2008,23(3): 87-89. (in Chinese) [11]刘增夕, 张鹏, 舒庆琏. 异性材料叠合梁研究[J]. 广西工学院学报, 1998,9(3): 24-26. Liu Zengxi, Zhang Peng, Shu Qinglian. A research of unlike materials coincidence beam[J].JournalofGuangxiInstituteofTechnology, 1998,9(3): 24-26. (in Chinese) [12]揭敏. 自由叠合梁中的弯矩计算[J]. 力学与实践, 1995,17(4): 64-65. Jie Min. Calculation research on bending moment of free coincidence beam[J].MechanicsinEngineering, 1995,17(4): 64-65. (in Chinese)
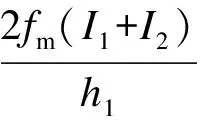

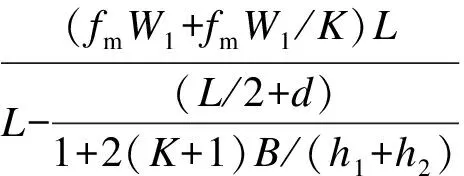


1.2 五架梁模型

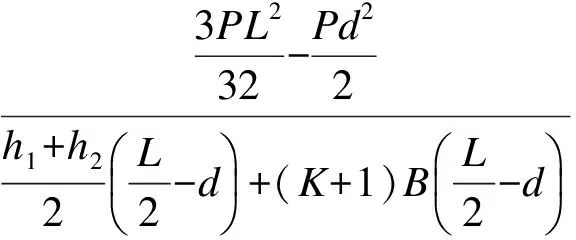

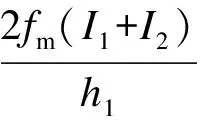


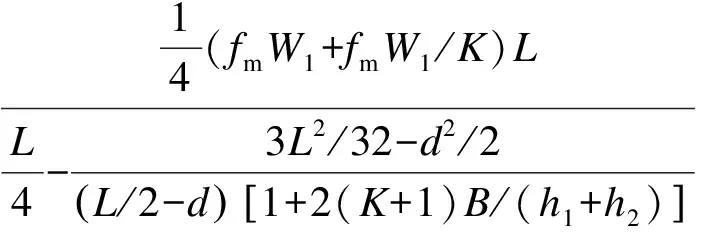
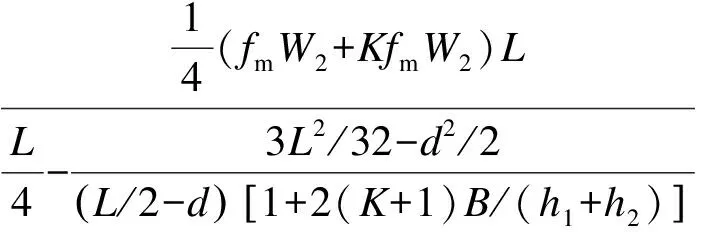
2 拼合檩条结构机制
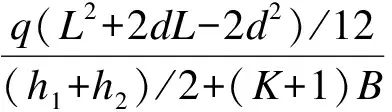
2.1 破坏模式1
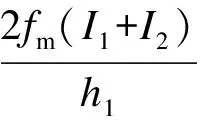

2.2 破坏模式2
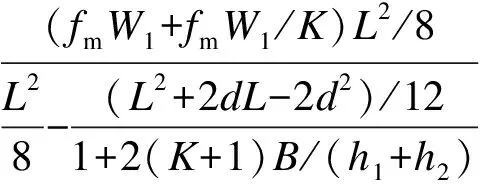

3 结论
