新型开洞软钢板阻尼器的理论及试验研究

李宗京 黄镇 李爱群

(东南大学土木工程学院, 南京 210096)

在过去的20年中,被动消能减震技术受到了高度关注并被广泛应用于工程实践中[1]．地震和风振作用实质上相当于能量的输入．通过在耗能减震结构中安装指定的耗能装置,使输入结构的能量转移到这些装置中被耗散掉,从而有效减小对结构本身的破坏[2]．金属阻尼器是被动减震领域中广泛应用的一种耗能装置．按照其耗能变形的方式,主要分为3类:① 利用金属轴向屈服变形耗能的阻尼器,如防屈曲支撑(BRB)[3];② 利用金属剪切屈服变形耗能的阻尼器,如剪切板阻尼器(SPD)[4];③ 利用金属弯曲屈服变形耗能的阻尼器,如加劲阻尼装置(ADAS)、三角形加劲阻尼装置(TADAS)等[5-6]．软钢材料由于具有较强的塑性变形能力和较低的屈服点,逐渐成为抗震用钢的一种重点钢种[7]．

本文设计制造了一种基于软钢板弯曲屈服变形耗能的开洞软钢板阻尼器,并针对其滞回耗能性能及核心性能参数进行了有限元数值模拟、理论分析及试验研究．

1 构造形式与滞回模型

开洞软钢板阻尼器主要由若干块相互平行的核心耗能板及顶板、底板构成(见图1)．宽w、高h、厚t的矩形耗能板采用软钢制作,并在其中部开设鼓形洞口,该洞口由两侧半径为r的半圆和中间宽度为b的矩形过渡段组成．耗能板与顶板、底板之间采用焊缝连接,阻尼器与支撑及框架梁之间采用高强螺栓连接．框架-支撑-阻尼器系统如图2所示．阻尼器随框架侧移而发生变形,从而产生弯曲塑性变形耗能．

图1 开洞软钢板阻尼器构造图

图2 框架-支撑-阻尼器系统

开洞软钢板阻尼器的滞回模型如图3所示．图中,点1为阻尼器的弹性极限点,对应弹性极限荷载Fe和弹性极限位移Δe;弹性直线段延长线与屈服平台段延长线的交点2为阻尼器的屈服点,对应屈服力Fy和屈服位移Δy;点3为阻尼器的设计最大工作位移点,对应最大阻尼力Fmax和最大位移Δmax．原点0与屈服点2连线的斜率表示初始弹性刚度K,且K=Fe/Δe=Fy/Δy;点2与点3连线的斜率表示屈服后刚度K′,且K′=γK,其中γ为屈服后刚度比．

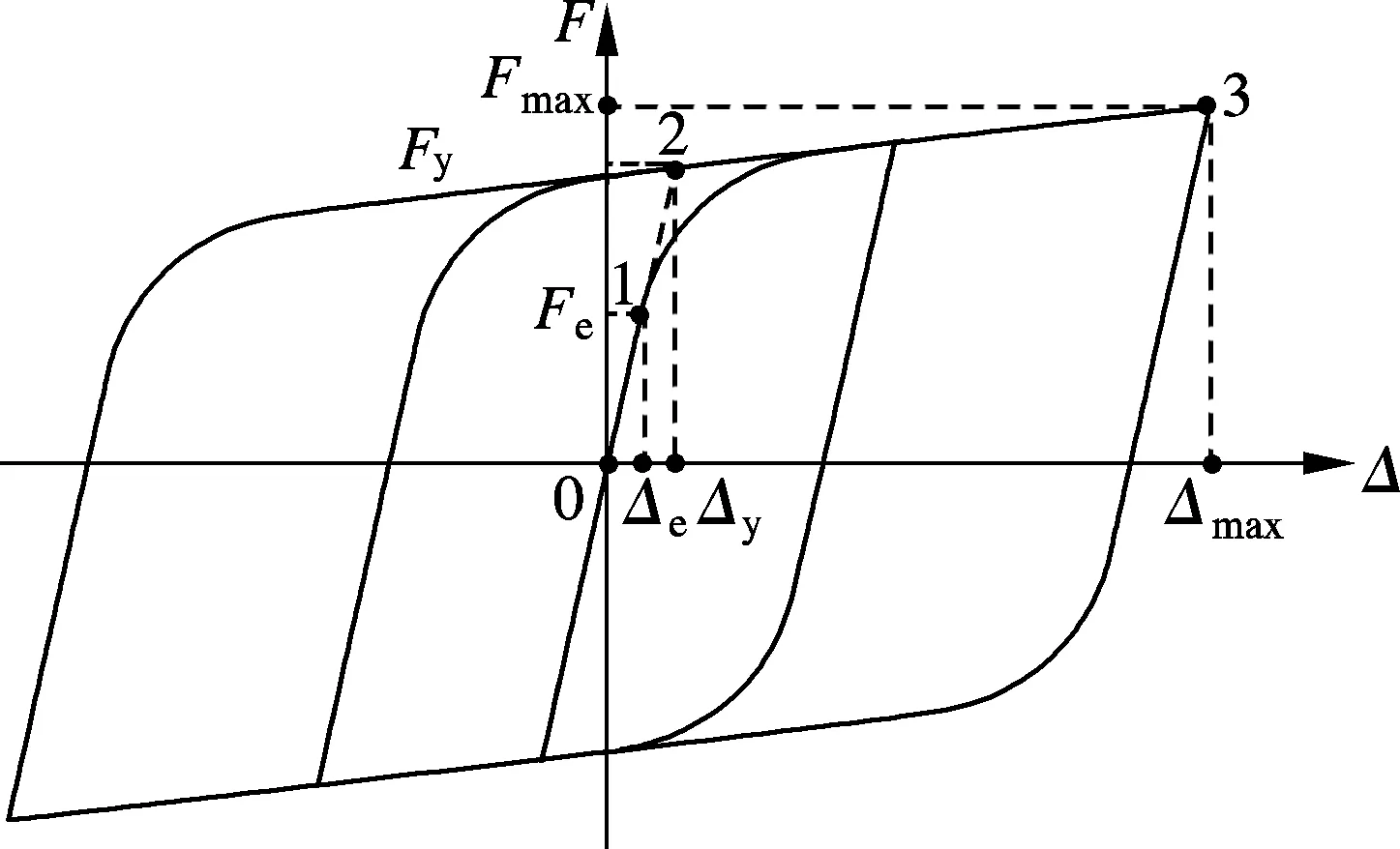
图3 阻尼器滞回模型

2 有限元数值模拟

采用通用有限元分析软件ANSYS对耗能钢板进行单调加载数值模拟分析．模型参数设置见表1．表中，fy为屈服强度.弹性模量E=206GPa,泊松比ν=0.3．

表1 模型参数

从图4(a)中可以看出,无开洞钢板应力呈两端大、中部小的分布趋势．发生变形后,其端部进入屈服状态,而中间大部分区域均处于弹性工作状态,耗能部集中于钢板上下两端,没有充分利用整块钢板的材料强度．根据无开洞钢板的应力分布云图,在钢板中部开设与应力云图纹理相一致的洞口,所得的开洞钢板应力分布云图见图4(b)．由图可知,应力分布状况得到改善．除洞口周边有少量未进入屈服的区域外,整块板均匀进入塑性屈服耗能,有利于提高其滞回耗能性能,并充分利用了整块钢板的材料强度．开洞板与无开洞板的荷载-位移曲线对比如图5所示．由图可见,二者的屈服力基本相同,前者的弹性刚度稍小于后者,屈服位移稍大于后者．综上所述,软钢耗能板开设洞口后,屈服力几乎保持不变,而应力分布状况优于无开洞板,可见开洞取得了较好的效果．

图4 Mises等效应力分布云图对比

图5 荷载-位移曲线

3 核心性能参数的理论分析

为了给阻尼器工程初步设计提供简洁并具有一定精度的参考公式，本节对阻尼器核心性能参数进行理论估算公式的分析推导.假设由n块耗能板构成的阻尼器弹性刚度为Kd,弹性极限荷载为Fde,弹性极限位移为Δde,屈服荷载为Fdy,屈服位移为Δdy．各块耗能板之间为并联关系,则

Kd=nK,Fde=nFe,Δde=Δe,Fdy=nFy,Δdy=Δy

(1)

3.1 弹性刚度

在阻尼器上下两端发生水平相对错动时,耗能板的变形形态、 受力状况及内力分布如图6所示．

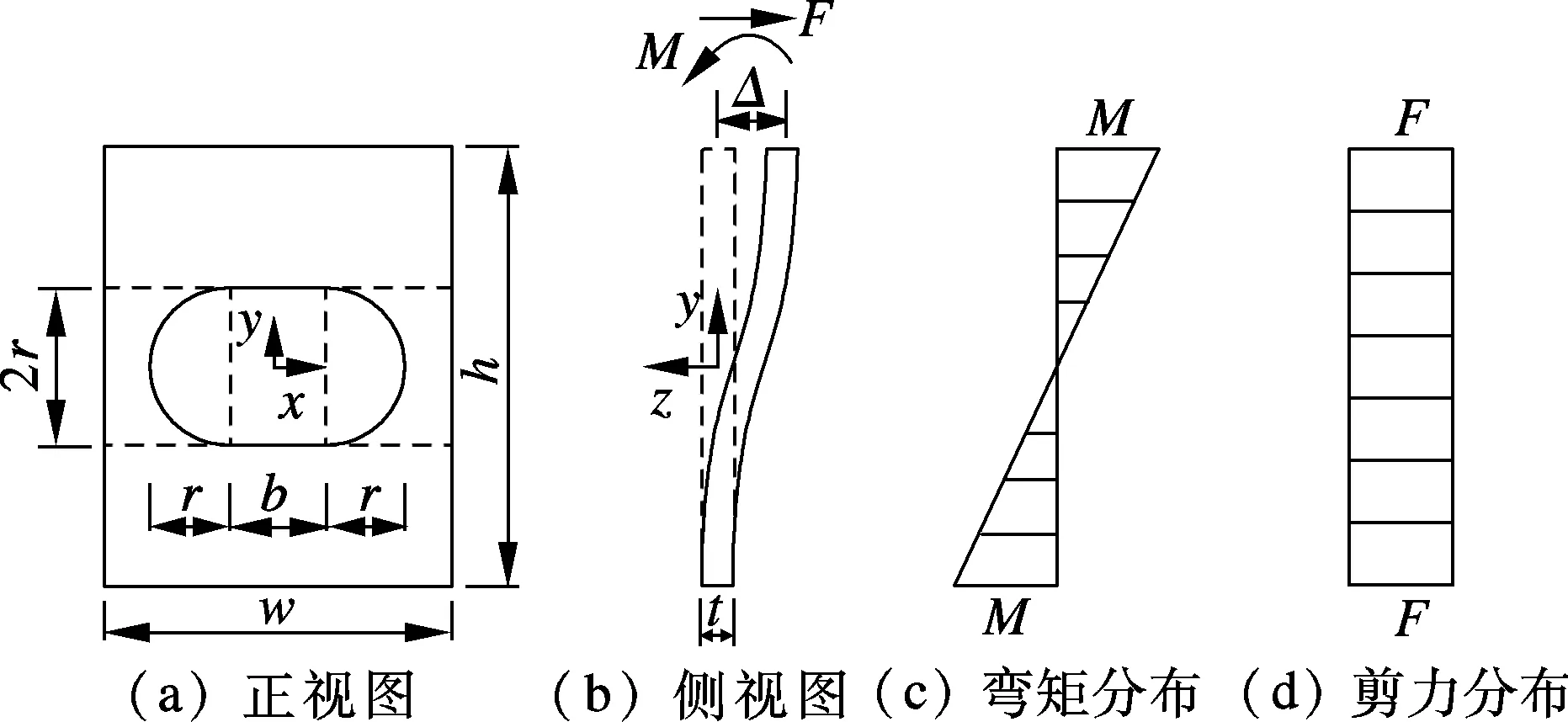
图6 阻尼器耗能板变形、受力及内力分布

图中,Δ为耗能板上下两端的相对水平位移,即耗能板的侧移量,F为水平力,M为力矩．耗能板可近似看作两端固支梁,考虑其弯曲变形和剪切变形的影响,可得[8]

Δ=ΔM+ΔV

(2)

式中,ΔM与ΔV分别为耗能板的弯曲变形和剪切变形所引起的侧移量．耗能板受到水平力F和力矩M的作用,可得

(3)

(4)

式中,E,G分别为钢材的弹性模量和剪切模量,取泊松比ν=0.3,则G=E/[2(1+ν)]≈ 0.4E;A为截面积;I为截面惯性矩;fs为截面剪应力分布不均匀系数,对于矩形截面fs=1.2;MP,VP分别为荷载在结构中引起的弯矩和剪力;MU,VU分别为单位荷载在结构中引起的弯矩和剪力,且MU(y)=y,MP(y)=Fy,VU(y)=1,VP(y)=F．

为便于积分,近似用等面积的矩形替代鼓形开洞,对式(3)、(4)进行积分计算可得

(5)

(6)

由于t很小,对比式(5)、(6)可知ΔM≫ΔV．结合式(2)可得

Δ=ΔM

(7)

故耗能板弹性刚度的理论公式为

(8)

3.2 弹性极限荷载与屈服荷载

耗能板达到弹性极限点时,耗能板顶端及底端附近表面开始进入屈服,则弹性极限弯矩为

(9)

由力平衡条件可得耗能板的弹性极限荷载为

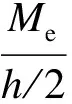
(10)

根据图3所示的阻尼器滞回曲线,设弹性极限点与屈服点之间的关系为

Fy=αFe,Δy=αΔe

(11)

式中,α为屈服点2与弹性极限点1之间的换算系数,且α>1,其经验取值需由有限元分析和试验研究确定．

由式(10)、(11)可得耗能板的屈服力为

(12)

3.3 弹性极限位移与屈服位移

基于弹性刚度K、弹性极限荷载Fe、屈服力Fy的理论计算式,结合K=Fe/Δe=Fy/Δy,可得耗能板弹性极限位移Δe与屈服位移Δy的理论计算式分别为

(13)

(14)

4 试验

4.1 试验模型与加载装置

对3组试件进行单调加载和低周往复加载试验,每组试件均由6块耗能板构成,其结构参数见表2．Damper1的耗能板由屈服强度为160MPa的软钢制成,Damper2和Damper3的耗能板由屈服强度为225MPa的软钢制成．

表2 试验模型结构参数 mm

试验采用MTS液压伺服系统加载．为避免加载出现偏心、扭转现象,采用“双剪”的加载模式,试验加载系统如图7所示．两边均对称布置3块互相平行的耗能板,故整套装置相当于一个含有6块耗能板的开洞软钢板阻尼器．

图7 试验装置

4.2 单调加载试验

单调加载试验得到的荷载-位移曲线见图8．根据第1节中的阻尼器屈服点确定方法,可得阻尼器Kd,Fdy,Δdy的有限元分析结果和试验结果．由式(8)、(12)和(14)可得耗能板性能参数K,Fy,Δy的理论计算值,结合式(1)可得阻尼器Kd,Fdy,Δdy的理论计算值,结果见表3．由表可知,Kd的理论值与有限元分析结果较为接近,偏差在10%以内，基本符合阻尼器工程初步设计的精度要求．α=2.0～2.5时,3组试件的Fdy,Δdy的理论值与有限元分析结果吻合较好．Fdy的试验值与有限元分析结果几乎一致,而Δdy的试验值稍大于有限元分析结果,Kd的试验值稍小于有限元分析结果．这主要是由于在试验过程中存在少量的夹具变形和螺栓滑移,导致Δdy的试验值偏大,并间接导致Kd的试验值偏小．

图8 单调加载试验曲线

4.3 低周往复加载试验

低周往复加载试验采用位移控制,并在每个控制点反复循环3圈,得到阻尼器滞回曲线(见图9)．由图可知,阻尼器试件的滞回曲线饱满,几乎没有捏缩现象,表现出稳定的滞回性能和较强的耗能能力．

变幅值往复加载后,为检验阻尼器的低周疲劳性能和持续耗能能力,继续在固定的位移幅值下对其进行往复加载试验．当位移幅值为30mm时,先后以0.1,0.3Hz频率分别往复加载30圈,再以1Hz频率往复加载直至破坏．以0.1,0.3Hz频率加载的荷载-位移曲线见图10．由图可知,在持续加载的前60圈内性能指标并未出现明显下降,符合《建筑抗震设计规范》(GB 50011—2010)对位移型阻尼器抗低周疲劳性能的相关要求[9]．3组试件均在加载到70～90圈时开始发生破坏．

表3 模型性能参数对比

图9 变幅往复加载滞回曲线

加载过程中,耗能板表现出较为明显的弯曲变形(见图11(a))．其表面首先出现裂纹,然后发生起皮现象(见图11(b)),最后在洞口四角方向发生断裂破坏(见图11(c))．

4.4 耗能指标

等效黏滞阻尼比是位移相关型阻尼器的重要耗能指标．定义等效黏滞阻尼比ζeq为[10]

(15)

图10 定幅往复加载滞回曲线

图11 试验过程照片

图12 等效黏滞阻尼比

图13 位移-等效黏滞阻尼比曲线

5 结论

1) 本文推导出的开洞软钢板阻尼器性能参数理论计算公式对其初步设计具有指导意义,可以通过调整耗能板的构造参数和块数来达到预期的阻尼器性能参数目标．

2) 开洞可使耗能板进入屈服后应力分布更加均匀,有利于提高阻尼器的抗低周疲劳性能，充分利用整块软钢板的材料强度,并且不对屈服荷载产生影响．

3) 开洞软钢板阻尼器具有饱满的纺锤形滞回曲线,几乎没有捏缩现象,表现出良好的延性和滞回性能,具有较强的耗能能力,能够持续稳定地耗能工作,符合《建筑抗震设计规范》(GB 50011—2010)对位移相关型消能器抗低周疲劳性能的相关规定．

4) 开洞软钢板阻尼器构造简单,安装方便,更换快捷,费用经济,性能优良,可广泛应用于现有结构以及待建工程的被动减振控制中．

)

[1]Housner G W, Bergman L A, Caughey T K, et al. Structural control: past, present, and future [J].JournalofEngineeringMechanics, 1997,123(9): 897-971.

[2]Soong T T, Spencer B F. Supplemental energy dissipation: state-of-the-art and state-of-the-practice [J].EngineeringStructures, 2002,24(3): 243-259.

[3]Xie Q. State-of-the-art of buckling-restrained braces in Asia [J].JournalofConstructionSteelResearch, 2005,61(6): 727-748.

[4]Chan W K, Albermani F, Williams M S. Evaluation of yielding shear panel device for passive energy dissipation [J].JournalofConstructionalSteelResearch, 2009,65(2): 260-268.

[5]Whittaker A S, Bertero V V, Thompson C L, et al. Seismic testing of steel plate energy dissipation devices[J].EarthquakeSpectra, 1991,17(4): 563-604.

[6]Tsai K C, Chen H W, Hong C P, et al. Design of steel triangular plate energy absorbers for seismic-resistant construction [J].EarthquakeSpectra, 1993,19(3): 505-528.

[7]Saeki E, Sugisawa M, Yamaguchi T, et al. Mechanical properties of low yield point steels [J].JournalofMaterialsinCivilEngineering, 1998,10(3): 143-152.

[8]Gere J M,Timoshenko S P.Mechanicsofmaterials[M]. 3rd ed. Boston: PWS-Kent Pub. Co., 1990.

[9]中华人民共和国住房和城乡建设部. GB 50011—2010 建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2010.

[10]Chopra A K.Dynamicsofstructures:theoryandapplicationstoearthquakeengineering[M]. Englewood Cliffs, NJ, USA: Prentice Hall, 1995.