非均质天然气藏的岩石物理模型及含气饱和度反演

巴 晶，晏信飞，陈志勇，徐光成，卞从胜，曹 宏，姚逢昌，孙卫涛

1 中国石油勘探开发研究院，北京 100083

2 清华大学周培源应用数学研究中心，北京 100083

非均质天然气藏的岩石物理模型及含气饱和度反演

巴 晶1，晏信飞1，陈志勇1，徐光成1，卞从胜1，曹 宏1，姚逢昌1，孙卫涛2

1 中国石油勘探开发研究院，北京 100083

2 清华大学周培源应用数学研究中心，北京 100083

非均质气藏中，天然气一般呈“斑块状”分布于含水岩石内部，这种非均匀分布特征会导致地震波显著的频散与衰减现象.为发展适用于碳酸盐岩储层中流体检测的岩石物理模型，本文基于Biot－Rayleigh波动方程，实现了对非饱和岩石的多尺度理论建模，预测了不同尺度下波响应与岩性、流体间的定量联系.将此项建模技术应用于阿姆河右岸的灰岩气藏，给出了多尺度的岩石物理学图板.通过与实验数据、测井精细解释结果及地震数据的对比分析，本文论证了图板的正确性与可适用性.结合叠后波阻抗反演与叠前弹性参数反演，基于地震资料进行了储层含气饱和度与孔隙度的反演，反演结果与各井实际的产气情况吻合.

岩石物理模型，Biot－Rayleigh理论，非均质，孔隙度，饱和度，气藏检测

1 引 言

近年来，为应对气候变化、发展低碳经济等问题，非常规油气资源，特别是强非均质性天然气资源，受到各国石油公司的高度重视.2011年，中国原油消耗量约为4.68亿吨，进口原油2.54亿吨，对外依存度54.3%，勘探利用天然气资源是缓解原油需求压力、保障国家能源安全的有效方式，然而，目前我国天然气储量绝大部分赋存于非均质气藏当中.

非均质气藏的储层孔渗关系复杂，岩石孔隙中不相混溶的气、水一般互呈“斑块状（补丁状）”分布.这种非均匀分布特征为实际的地震勘探工程带来了难度.为发展非均质气藏的地震检测技术，以期在复杂的储层环境中精确地定位富气“甜点”，首先需要查明的是气、水非均匀分布的储层岩石中的地震波传播及响应规律.

Gassmann与Biot最早针对孔隙含流体的多孔介质中的地震波传播机理进行了研究，即Biot－Gassmann理论［1－3］.然而传统Biot－Gassmann理论主要考虑的是饱和一种流体的均一孔隙结构，不能描述实际储层的复杂情况.White等（1975）考虑了岩石内部同时含气、水的情况，其中气体呈“补丁状”分布于含水岩石的背景下［4］.Dutta等（1979）改进了White理论的不足，使其在低频极限下预测的纵波速度吻合于由经典Biot理论出发所导出的分析结果［5－6］.为解决相同的问题，Johnson提出了一种分支函数法，这种方法在低频与高频极限分别对非饱和介质中波的频散与衰减进行分析，而在中间频段则采用复变函数的方法进行近似逼近，实现了对不同频段内非饱和介质波传播规律的模拟［7］.近十年来，Müller、Gurevich与Toms等对一维与三维的随机非饱和介质进行了模拟，并将模拟结果与碳酸盐岩与砂岩的实测数据进行对比，认为这种随机介质数值模拟的方法也能为实际岩石的波响应提供合理的描述及预测［8－10］.

聂建新等（2004）在Biot／Squirt模型［11］（简称BISQ模型）中引入了对流体非饱和情况的考虑［12］，聂建新、巴晶等（2012）则同时考虑了岩石内部由泥质引起的黏弹性以及流体非饱和对BISQ模型中波传播的影响［13］，但在两相流体的处理中，这些工作假设气、水完全均匀地混合.刘炯等采用孔隙介质力学的方法，研究了球状补丁及水平交替层状的非均匀、非饱和岩石模型中的地震波传播规律［14－15］，然而这种做法的数值计算与实现过程较繁琐，不利于直接的工程应用.

2004年，Pride、Berryman等提出了一种物理意义更加明晰的理论——双重孔隙介质理论（简称双孔介质）——来分析非饱和介质中的弹性波传播及衰减规律［16］，在这种情况下，所谓双孔即分别对应于非饱和岩石中的含气孔与含水孔.巴晶、曹宏等对双重孔隙介质中的地震波进行了进一步的模拟与分析［17－20］，将双孔理论的预测结果与川中须家河组致密砂岩的宽频带实验结果进行了对比，证实了此类储层中弹性波在地震勘探频段内可能出现强烈的频散现象.为进一步推导一种格式尽可能简洁、物理参数尽可能少、各参量均具备物理可实现性的波传播方程，以期满足实际的应用研究与工业生产的需要，巴晶、Carcione等基于Biot理论框架，导出了描述非饱和岩石地震波传播机理的Biot－Rayleigh方程（简称B－R方程）［21－22］，通过与前人理论的对比，成功将这种方程应用于实际气藏勘探的工程问题中［23］.孙卫涛、巴晶、Carcione、Müller等则基于南澳Casino砂岩的实验数据与扫描结果进行了进一步对比，针对砂岩储层讨论了B－R方程的合理性［24］.

对于非均匀、非饱和的实际储层，迄今文献中还未出现一个能普遍地被各研究机构、产业部门所接受的有效的地震波理论.如何将复杂的理论与繁琐的公式应用于实际的工程问题，这个过程本身就面临困难.目前已知的岩石物理建模技术在流体替换中采用Gassmann理论，忽略了非均匀性与波的频散，仅能制作单一尺度的岩石物理图板，其用途主要是横波预测与辅助定性解释.本文基于前期的理论结果，将结合岩石基质、骨架建模及流体替换三个步骤，给出针对实际储层的岩石物理建模流程.以阿姆河右岸的灰岩气藏为例，将制作的多尺度岩石物理图板与实验数据、测井解释结果、地震数据分别进行对比.最后基于岩石物理图板，结合叠前地震反演结果进行储层孔隙度与饱和度的反演，将反演结果与各井的试油情况进行对比，并给出结论.

2 Biot－Rayleigh方程

Berryman在20世纪90年代即考虑了岩石内部存在两类孔隙的情况，导出了双孔介质的基本波动方程［25－26］，即三个公式组成的方程组，然而，该方程组未能考虑地震波激励下流体在两类孔隙间的弛豫作用，因此仅相当于两组单孔Biot方程的简单叠加，其计算的纵波频散、衰减与传统Biot理论处于同一量级，远低于实测结果.同样的问题也发生在由Santos等提出的固、液、气三相理论［27－28］当中，赵海波（2007）为改善Santos理论对岩石纵波衰减的预测能力，曾将黏弹性理论引入这种理论中［29］.

Pride与Berryman（2004）对三式的双孔方程进行了完善，引入了一个附加的公式描述波激励下的局部流体荡动，所采用的方法类似于Johnson的分支函数法［7，30］.这种双孔理论的缺陷在于复杂的方程、过多的待定参数不利于工程应用.唐晓明等推导了孔隙－裂缝双孔介质中的波传播方程，并将这种方程应用于声波测井的工程问题中［31－32］.

为采用更简洁的方程描述地震波激励下，非均质岩石内部复杂的流体振荡以及弛豫过程，根据Rayleigh理论的思路［33］描述各向同性的流体局部荡动，所导出的B－R方程组如下所示［21］：

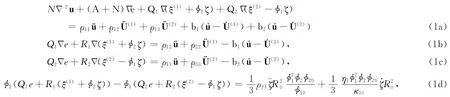
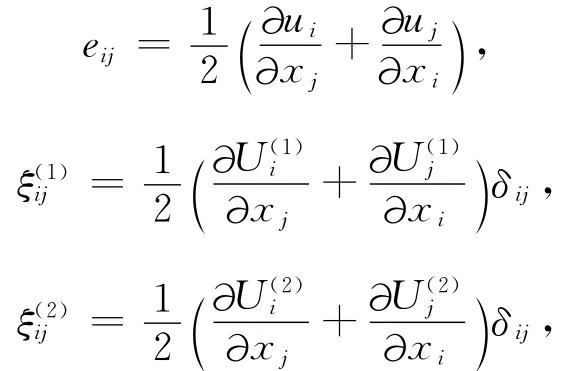
其中x1，x2与x3分别表示三个方向的坐标.φ1和φ2表示两类孔隙的绝对孔隙度，岩石的总孔隙度φ＝φ1＋φ2；φ10与φ20分别表示两个区域内的局部孔隙度，如岩石内部仅含有一种骨架，但却饱和有两种流体，则φ10＝φ20＝φ.ρf1和η1表示背景相流体的密度与黏度.R0表示气泡半径，κ10表示岩石渗透率.

文献［23］详细论证了式（1）在非饱和岩石地震波传播问题中的适用性，并给出了弹性参数A、N、Q1、R1、Q2与R2，密度参数ρ11、ρ12、ρ13、ρ22与ρ33，耗散参数b1与b2的确定方法（详见附录）.对（1）式采用平面波解析解分析的方法，求解一元三次的复方程组，可得三类纵波的速度与衰减系数，其中速度最高的快纵波即对应常规勘探的纵波.

3 岩石物理模型及流程

3.1 岩石的基质与干骨架

针对实际的含油气储层进行岩石物理建模一般包括三个步骤［34－35］：（1）分析岩石基质的矿物组分与配比，计算基质的弹性参数与密度；（2）采用理论、经验公式或其他方法，基于岩石基质的性质、储层的孔隙结构、骨架的固结程度等因素，计算岩石骨架的弹性参数与密度；（3）分析储层环境下流体的物理性质，结合流体的分布特征及其与孔隙结构的联系，估算含流体岩石的波响应特征，并与实际的工程问题相联系.

处理岩石基质成分常采用的办法有：Voigt－Reuss－Hill平均法、Hashin－Shtrikman－Hill平均法、时间平均方程等［36］.组分与组合较为复杂的情况下可采用自洽理论进行估算，对于组分较为单一、结构较紧密的岩石，如方解石含量达90%以上、泥质及其他矿物含量很低的较纯的灰岩，则采用Voigt－Reuss－Hill平均，即可得到理论的估测值，本文建模沿用了这种方法，如（2）式所示.其中Mg表示基质弹性模量，fi与Mi表示第i种矿物的体积率与弹性模量，N表示岩石中矿物的种类数.

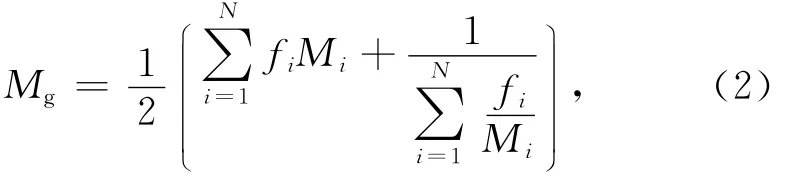
得到岩石的基质参数，建模过程中一个重要的步骤在于估计岩石干骨架的弹性模量Kb.由于对Kb进行流体替换即得到储层的地震波响应特征，因此Kb精确与否直接关系到岩石物理模型的适用性.Xu等采用差分等效介质理论［37］与Kuster－Toksöz理论［38］对砂岩与碳酸盐岩进行建模.本文采用Pride提出的一种半经验公式进行干骨架的建模，如（3）式所示.

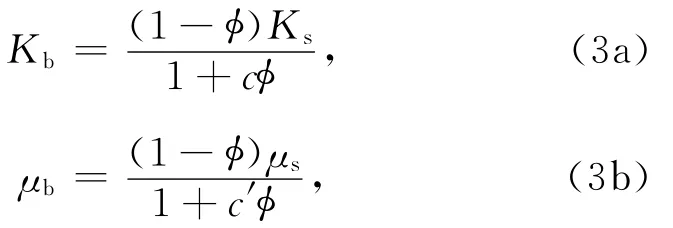
其中μb表示骨架剪切模量，Ks与μs表示基质体积与剪切模量，经验参数c、c′与岩石的固结程度有关.

以灰岩为例，若岩石基质主要由方解石构成，选定不同的固结参数c与c′，则岩石干骨架的体积与剪切模量随孔隙度的变化关系如图1所示.岩石干骨架的弹性参数随孔隙度上升而下降，若岩石的固结程度变弱，这种下降的趋势更加明显.岩石的固结程度可根据储层的具体情况确定.

3.2 流体替换

基于岩石的基质与干骨架参数，对孔隙空间中的流体进行替换，可分析不同流体、不同饱和度情况下岩石的地震波响应特征.由于孔隙流体的影响，相同的岩石中不同频段的纵波传播速度存在显著差异，体现在多尺度地震波资料中即纵波的频散效应［39］.采用B－R方程，可预测多尺度波形资料中各个频段内的纵波传播速度.

仍以灰岩为例，设岩石骨架的参数为：孔隙度0.16，骨架体积模量24.81GPa，骨架剪切模量11.79GPa，渗透率为30.23mD，平均气泡尺5mm.岩石基质为方解石，储层温度、压力下的流体密度及弹性参数可根据van der Waals公式估算［23］.图2给出了不同频率下非饱和灰岩中纵波速度及衰减随含水饱和度的变化关系.对于同一块灰岩，不同频率下纵波速度随含水饱和度的变化关系有明显差异，在低频段，纵波速度曲线呈典型的“勾形曲线”，在超声波频段，纵波速度随含水饱和度的增加近似线性地单调上升.本例中最强的纵波衰减出现于声波频段，发生于含水饱和度85%～95%之间.在中、低频段，纵波衰减主要出现于高含水饱和度的情况下，此外，速度曲线的最低点与衰减曲线的峰值随频率的上升向含水饱和度轴的左端移动.

3.3 岩石物理建模流程

针对实际储层情况，基于理论、经验认识与实验观测对岩石的基质、干骨架与孔隙流体进行分析，给出地震波响应特征与岩性、孔隙与流体之间的定量联系，即岩石物理学建模.

图3给出了岩石物理学建模的流程图.在实际工程中进行岩石物理建模与分析，一般肯定需要对基于理论与经验得到的初始模型进行反复调试，调试过程中主要参考的依据信息包括测井资料、测井解释成果、地震叠前与叠后的反演结果、部分井的试油结果.如果能对目的层针对性地开展岩石物理实验，将有利于提高模型的精度.在无法获得充分的岩芯及实验数据的状况下，可适度参考前人已发表的岩石实验数据，但前提是岩石性质与工区目的层有可比性.

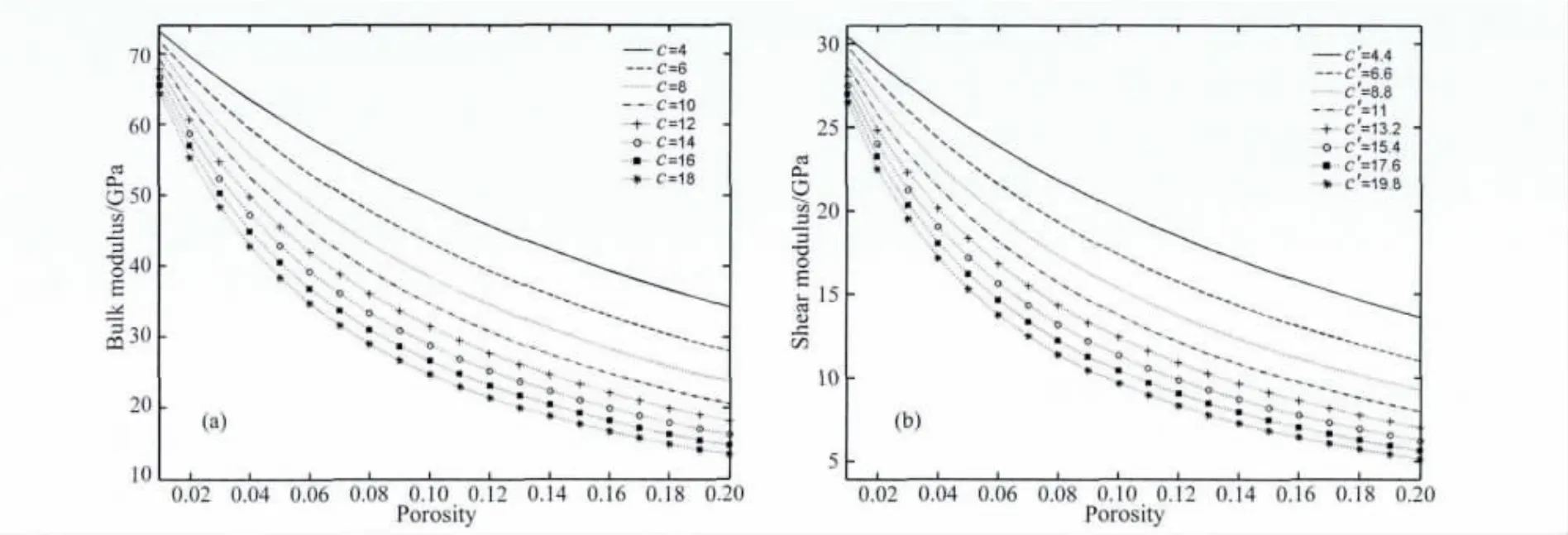
图1 灰岩干骨架弹性模量随孔隙度的变化关系（a）体积模量；（b）剪切模量.Fig.1 The relationships of dry rock elastic moduli versus porosity in limestone（a）Bulk modulus，（b）Shear modulus.

图2 非饱和灰岩中不同频率纵波速度及衰减随含水饱和度的变化关系（a）纵波速度；（b）纵波衰减.Fig.2 The relationships of P－wave velocities and attenuation at different frequencies versus porosity in partially－saturated limestone（a）P－wave velocities；（b）P－wave attenuation.

4 气藏的应用实例

4.1 工区概况

麦捷让地区位于阿姆河右岸区块坚基兹库尔构造带，为近东西走向的背斜构造，断裂不发育.所研究之目的层位于上侏罗统卡罗夫－牛津阶碳酸盐岩地层.储层发育环境为开阔台地，为台内礁滩相储层，沉积相包括台内生屑粒屑滩、滩间海，台内礁等，有较强非均质性.

本区块灰岩储层主要发育于XVm层，储层岩性主要为生屑灰岩、球粒灰岩、鲕粒灰岩和团块灰岩，为中高孔－中渗孔隙性储层［40］.疏松、多孔的灰褐色灰岩基质的主要成分为方解石与微量泥质，局部层段含微量的白云石与石膏，孔隙内常见亮晶方解石胶结，局部形成溶蚀孔洞.储层孔隙度分布范围是0.18%～24.1%，平均值7.09%；渗透率范围是0.0006～389mD，平均值2.18mD.在岩石物理建模的过程中，主要考虑的基质组分是方解石与泥，优质储层的孔隙度在8%以上.

4.2 多尺度岩石物理学图板及其校正

采用如图3所示流程对麦捷让地区XVm层灰岩建模，以方解石与微量泥质作为基质，采用式（3）计算不同孔隙度情况下干岩石骨架的弹性模量，而在不同的波频率下，对式（1）进行平面波分析可得到不同尺度的纵波速度.在计算横波速度的过程中，一般可忽略流体对横波频散的影响.最终基于多尺度的纵波速度、横波速度，可形成岩石物理学的图板.如图3所示，对岩石物理学图板的校正主要依据实验数据、测井结果与地震数据.

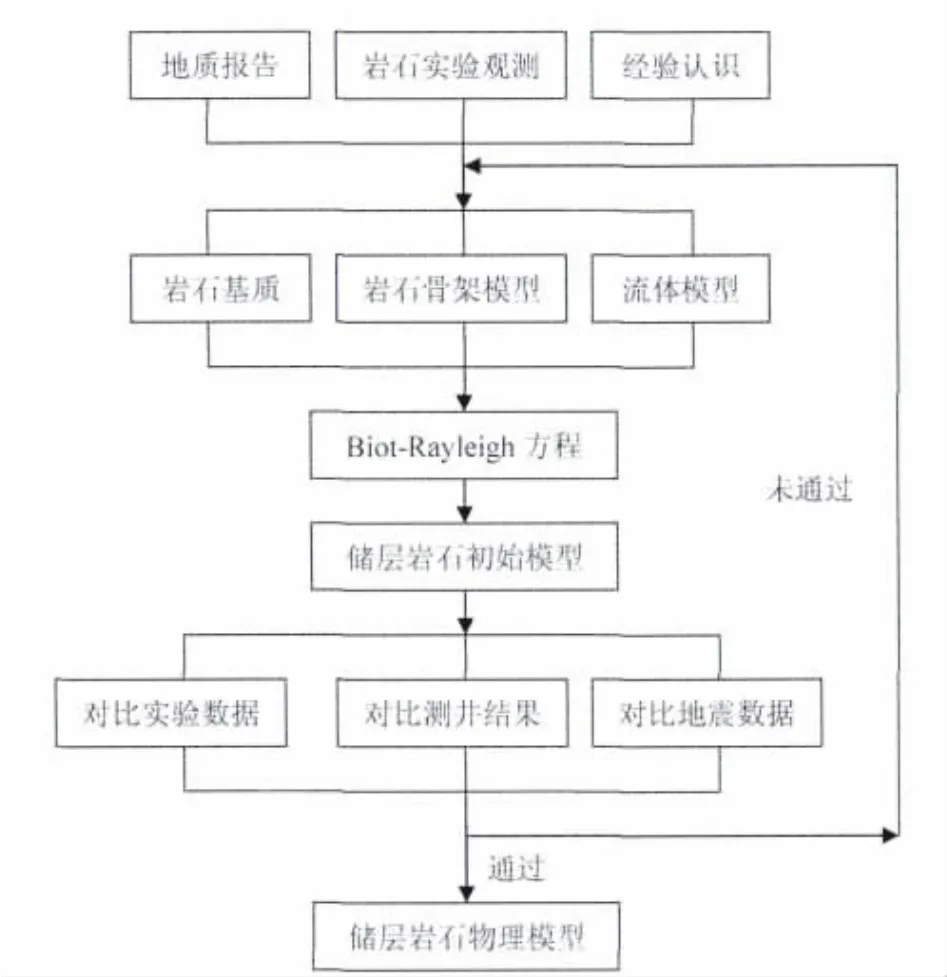
图3 岩石物理学建模流程图Fig.3 The flow diagram of rock physics modeling

在输出最终岩石物理图板前，必须在不同频段对比当前图板与对应的实测波响应数据，调节各输入参数，使岩石物理图板与实验数据的分布规律一致.基于实验数据校正图板，要确保与储层岩性相近的样本的数据散点的连线与图板对应孔隙度的经线接近甚至重合，且完全含气与含水的实验数据点尽量接近饱气与饱水纬线.基于测井与地震数据校正图板，需将数据投影至图板上，调节计算的输入参数，保证前期解释的气层、水层的数据点接近图板的下、上经线，若有孔隙度的解释结果，还须保证数据的孔隙度分布规律与纬线情况一致.校正对实测数据的可靠性有依赖.

如图4所示，给出了超声波频段的岩石物理图板与实验数据的对比结果.图4中碳酸盐岩的实验数据选自文献［41］与［42］，主要为灰岩.文献［41］报告了在800kHz频率下对完全饱水与干燥的碳酸盐岩进行的观测，文献［42］报告了在500kHz频率下对不同含水饱和度的灰岩进行的观测，因此前者数据仅包含同一块灰岩饱水与干燥（接近于饱气）两个数据点（其干燥岩石的体积模量采用了Gassmann方程反替换得到），而后者数据包括多个饱和度下的测量结果.对各样本情况归纳如表1所示，其中样本A、C选自文献［42］，B、D、E、F选自文献［41］.

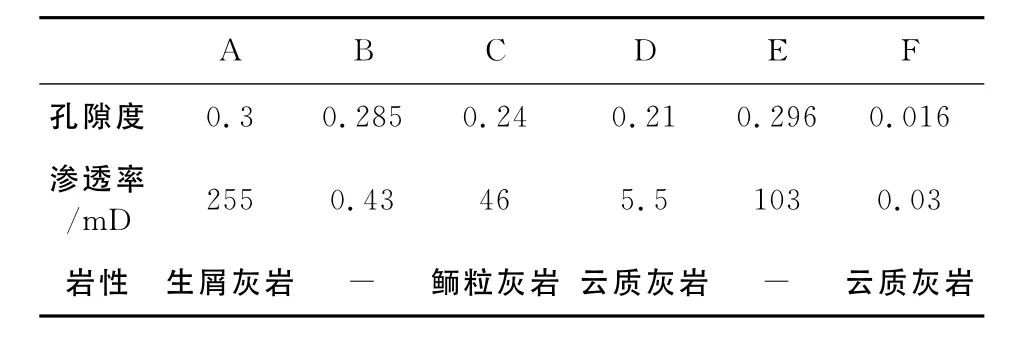
表1 各岩石样本情况表Table 1 Physical properties of the rock sampls

对比图板与实验数据显示，部分样本（A、B、C）的观测结果与采用本文方法对麦捷让XVm层灰岩生成的模板吻合较好，样本D次之，这些样本（各样本孔隙度恒定）的实验数据随孔隙度的分布，与岩石物理模板的经线吻合很好，其中样本A、C与图板吻合最好，这是由于本图板是根据麦捷让XVm层灰岩建立的，而样本A、C与目的层生屑、鲕粒灰岩的岩性最为接近.实验数据中波响应随饱和度的变化规律与纬线相同，且波响应从饱水到饱气间的变化幅度也与模板基本一致.以上情况说明，虽然这些样本并非采自目标区，但一些灰岩中共性的地质特征、结构特征与孔隙流体分布特征，使得相似的岩石物理模板可能适用于不同地区的灰岩，并且相互间起到借鉴与校正作用.

样本（E、F）与岩石模板不吻合，其中样本E观测的纵波阻抗明显高于同孔隙度下的理论模板值，样本F观测的纵波阻抗明显低于同孔隙度的理论模板值，这与各岩样矿物组分及结构特征有关（岩样F为致密云质灰岩，岩样E也可能含石膏等杂质，与建立图板的目的层岩性不符）.样本F的纵横波速度比很低，与图板差异明显，内部可能存在裂隙.考虑到实际碳酸盐岩储层孔隙结构的多样性及复杂性，试图采用一种模板去描述所有的实测现象是不可能的.在当前的阶段，本文只能选定具体储层，针对具有一定统计学普遍意义的“岩石样版”进行建模与反演，多解性问题是无法彻底解决的.

如图5所示，给出了校正后声波频段的岩石物理图板（孔隙度0.08～0.2范围段）与Met－22井部分储层段的测井水饱和度解释结果的对比，其中测井散点的波阻抗与纵横波速度比是基于测井观测的声波时差计算得到.图5中，部分测井数据分布于岩石物理图板之外，这是由碳酸盐岩内部孔隙结构与流体分布的复杂性决定的.按色标显示的纵波阻抗、纵横波速度比随含水饱和度的变化规律，完全饱水的测井数据点基本接近模板饱和度为1纬线，接近完全饱气的数据点基本沿饱和度0的纬线分布.高孔隙度范围内（0.13～0.19）测井解释的饱和度有两极分化的趋势，与模板在边界附近吻合更好.低孔隙度范围内（0.08～0.13）测井解释的饱和度渐变性规律更明显，与模板在中间段吻合更好.

图5中测井数据点的总体分布与气藏的发育情况有关，图板左端与右端测井数据点随含气饱和度的分布规律不同，可能受测井解释中采用的计算方法影响，此外储层孔隙度高的区域渗透性好，气水运移较易实现，常出现气水分异明显的情况，而低孔隙度区域渗透性差，气水分异不明显，则多产生中、低含气饱和度储层，这在川中须家河低孔砂岩中也很常见.

如图6所示，对比了校正后地震频段下的岩石物理图板与叠后、叠前地震反演数据体中提取的地震数据.数据选自工区Met－22、23井附近地震道，按初期解释结果，储层被划分为水层、气层与非储层三类［40］，结合两口井的测井解释结果及试气情况，在井震标定后，在XVm层顶界附近选取了部分对应水层、气层与致密层的地震数据，地震数据选取过程中不能彻底排除误判的可能.

图6对比显示，水层地震数据基本沿含水饱和度1的维线分布，部分点纵横波速度比高出图板上边界，气层地震数据的纵横波速度比呈现较宽的分布范围，并对应图板中含气饱和度纬线的变化范围在30%～100%之间.部分气层的数据点纵横波速度比低于图板下边界.在孔隙度0.12～0.15之间（主力储层段），地震数据点与模板的吻合最好，因此基于该模板对储层含气性进行检测是可行的.非储层数据点分布的孔隙度范围在0.05以下，前期针对目的层的地质学研究曾将储层孔隙度下限划定为0.05，地震解释与反演工作中采用的下限略高于此数值，图中对比显示，岩石物理模板能很好地区分所定义的储层与非储层.

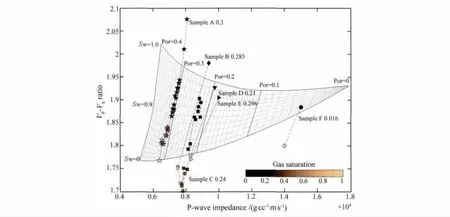
图4 超声波频段（＞500kHz）碳酸盐岩岩石物理图板与岩石实验数据的对比（色标表示含水饱和度；色深表示含水饱和度高，色浅含气饱和度高）Fig.4 Comparison between carbonate rock physics template and experimental data in ultrasonic band.The colorbar indicates water／gas saturation，where darker color is for higher water saturation and lighter color is for higher gas saturation

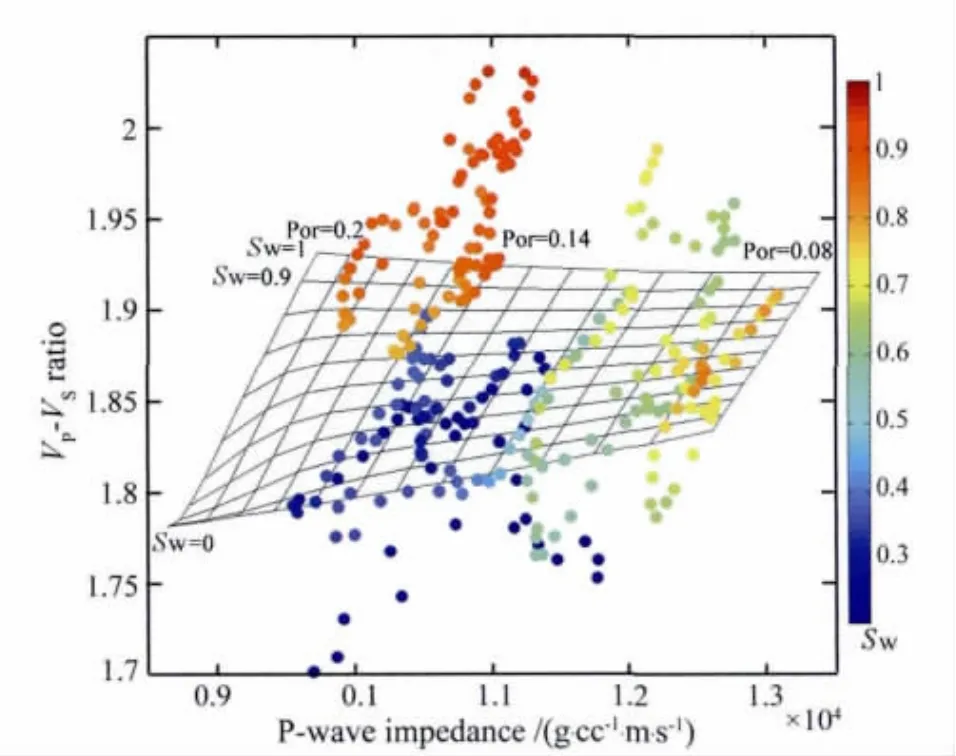
图5 灰岩岩石物理图板与测井解释结果的对比.色标表示含水饱和度Fig.5 Comparison between limestone rock physics template and sonic log interpreted data in sonic band.The colorbar indicates water saturation

4.3 孔隙度与含气饱和度的预测结果

图6 灰岩岩石物理图板与地震数据的对比.图中黄、蓝、粉红色标表示气层（含差气层）、水层与非储层，为前期地震解释认识Fig.6 Comparison between limestone rock physics template and seismic inverted data in seismic band The yellow，blue and pink color denote gas reservoirs（including poor gas reservoirs），water reservoirs and non－reservoirs，respectively，which are the conclusions of previous seismic interpretation.

基于4.2节的分析结果，得到适合于描述目的层非饱和灰岩的地震响应特征的岩石物理模板，根据地震尺度模板，采用常规叠前地震反演输出的纵波阻抗与纵横波速度比信息，可将实际的地震响应与岩石的孔隙度、饱和度联系起来.

基于岩石物理建模得到地震频段的图板.首先对目的层段进行叠后与叠前反演，得到波阻抗与纵横波速度比数据体，提取目的层的波阻抗、纵横波速度比数据逐点投影到模板上，判断距投影点最近的模板格点，在最小二乘残差低于一定门槛的情况下，最近的模板格点的孔隙度、饱和度即为所对应的储层位置的孔隙度、饱和度反演值.基于这种方法可定量预测储层物性甚至直接检测烃类.

在目的层内，投影点在图板外且与边界经线差异较大的情况下，一般做非储层处理，此时孔隙度与饱和度被置零.反演中主要考虑的是目的层段的主力灰岩储层，图板之外的包括孔隙度过低的致密灰岩、泥岩、低孔泥灰岩、石膏等并非勘探目标，因此直接可作为非储层处理.

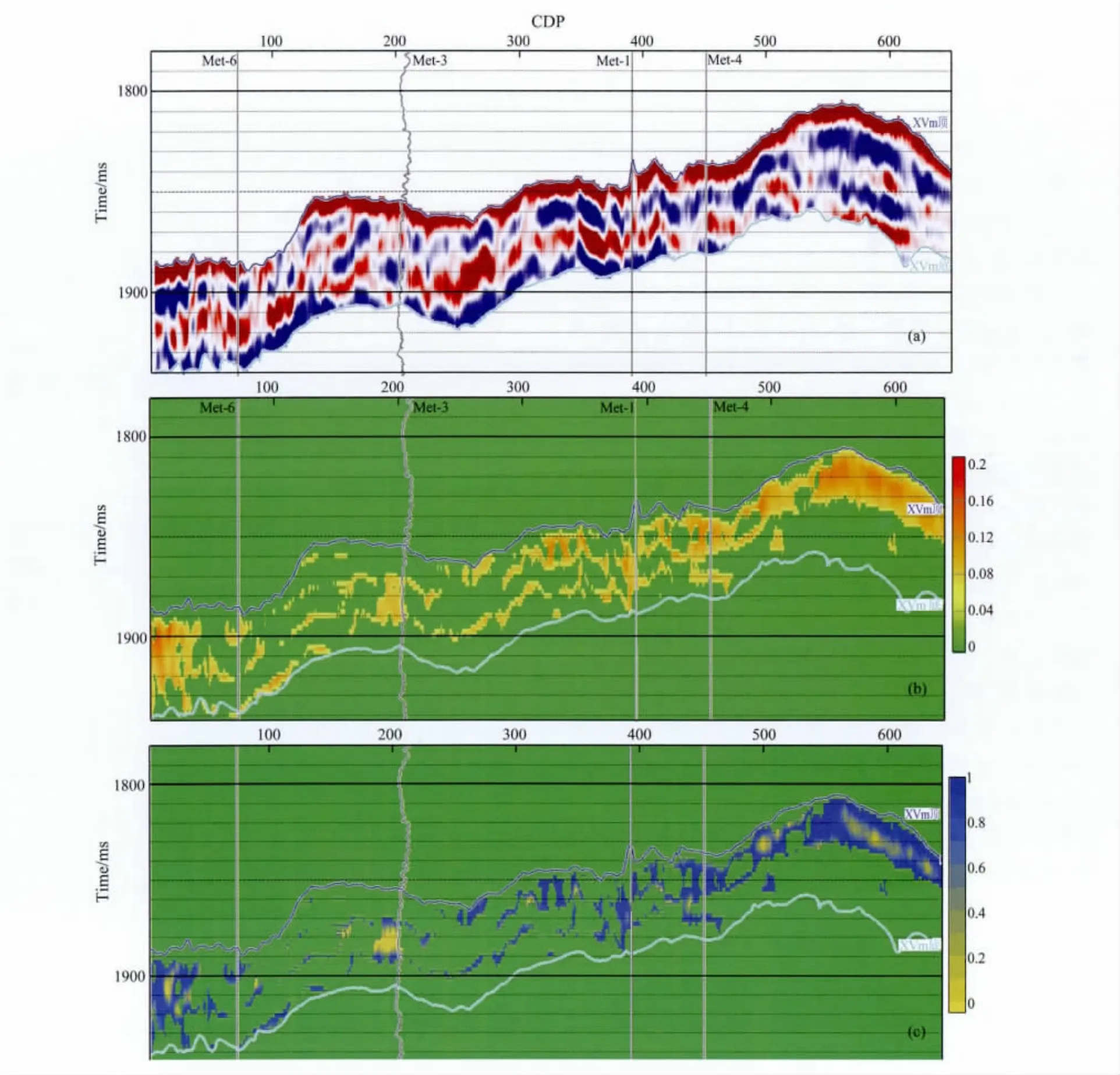
图7 过Met－6、Met－3、Met－1、Met－4井二维线地震资料与反演结果（a）叠后地震资料；（b）储层孔隙度反演结果；（c）储层含水饱和度反演结果.Fig.7 The seismic data and inversion results of a 2Dline crossing the 4wells of Met－6，Met－3，Met－1and Met－4（a）Post－stack seismic data；（b）Inversion results of reservoir porosity；（c）Inversion results of reservoir water saturation.

基于叠后与叠前反演得到的波阻抗、纵横波速度与密度，在XVm顶、底界之间采用岩石物理图板，图7给出了一条过井线的孔隙度、饱和度反演结果，其中井Met－3为工业气井，测有声波速度，Met－1、4、6无声波测井结果.如图7中，Met－3井的反演结果同样显示较强的含气性（黄色区域显示），Met－1、4井次之，有微弱的含气性显示，Met－6井最差，时间剖面上仅显示有少量水层（蓝色区域显示），对比试油结果中Met－3井为高产气井，Met－1、4为低产气井，Met－6为水井，与孔、饱反演剖面均一致.对于目的层灰岩，文献［40］给出了基于岩石物理模型进行定性的储层含气性检测得到的结果，本文采用多尺度观测数据制作了对应图板，并进行了储层孔隙度、饱和度的定量反演.在以图7为例的四条线反演结果中，孔、饱反演结果均与各井试气情况吻合.常规的岩石物理建模往往基于单一尺度数据（一般采用测井数据），且主要用于反演之后辅助解释储层及流体.本法采用了多尺度数据，所生成之模型可定量地用于流体检测，但缺点在于，模型的建立对实测数据可靠性要求很高.

5 结 论

为解决碳酸盐岩储层的波传播及岩石物理建模问题，基于岩石的基质参数，采用Pride公式对岩石的干骨架进行建模，采用Biot－Rayleigh方程进行流体替换，结合实际的勘探应用，提出了一种多尺度的岩石物理建模流程（图3）.针对阿姆河右岸麦捷让地区XVm层的灰岩气藏，进行了岩石物理建模，将最终输出的岩石物理模板与不同尺度下的实验数据、测井数据及地震数据分别进行了比对，结果显示模板与各尺度波响应数据的分布规律基本一致，能够定量地将储层地震响应与岩石的孔隙度、饱和度联系起来.基于叠后与叠前地震反演，估算了实际储层的孔隙度与饱和度，过井线的反演结果与各井的实际产气状况基本吻合.

本文针对非饱和灰岩气藏提出了一种岩石物理建模技术，这种方法主要适用于描述基质组分较单一的孔隙（洞）型储层，且本文建立的岩石物理图板主要针对麦捷让地区的XVm层灰岩.对于更加复杂的储层情况，岩石物理模型的研究有待进一步深入.若期望解决不同岩性、不同结构与不同流体所带来的各类问题，岩石物理图板必须针对性的进行调整.试图采用一种恒定的模型去描述所有储层的地震响应，是难以实现的.

致 谢 本研究受中国石油勘探开发研究院科研管理处、团委与人事劳资处“师带徒”培养计划支持.论文完成过程中卢明辉、李劲松、张兴阳与作者进行了有益讨论，刘晓虹进行了测井资料的精细解释，这里一并表示谢忱.

附录 Biot－Rayleigh方程相关参数的确定方法

式（1）中的6个Biot弹性参数的确定方法

如下：

其中Ks、μs为岩石基质的体积模量与剪切模量，Kb、μb为岩石骨架的体积模量与剪切模量，为背景相（一般为水孔）与嵌入体（一般为气孔）中两种流体的体积模量.

式（1）的5个Biot密度参数的确定方法如下：

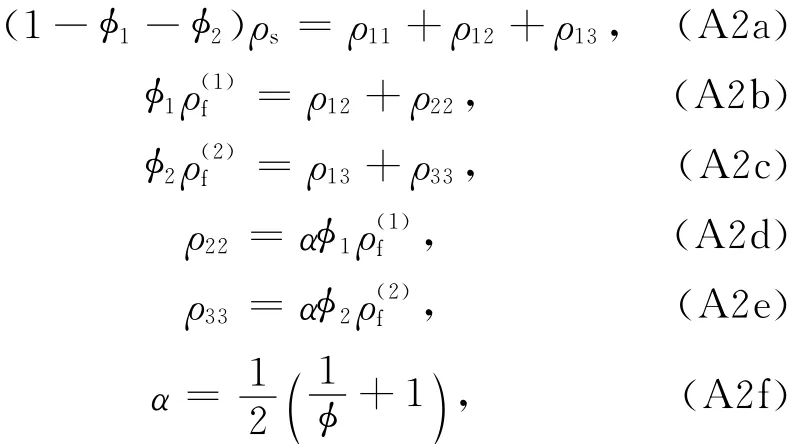
式（1）中的2个Biot耗散参数的确定方法如下：

其中η（i）表示两种流体的黏度，κ为均一骨架的渗透率.

（References）

［1］ Gassmann F.Über die Elastizität poröser Medien.Vier.der Natur.Gesellschaft in Zürich，1951，96：1－23.

［2］ Biot M A.Theory of propagation of elastic waves in a fluidsaturated porous solid：I.Low－frequency range.J.Acoust.Soc.Am.，1956，28（2）：168－178.

［3］ Biot M A.Theory of propagation of elastic waves in a fluidsaturated porous solid：II.Higher frequency range.J.Acoust.Soc.Am.，1956，28（2）：179－191.

［4］ White J E.Computed seismic speeds and attenuation in rocks with partial gas saturation.Geophysics，1975，40（2）：224－232.

［5］ Dutta N C，Seriff A J.On White’s model of attenuation in rocks with partial gas saturation.Geophysics，1979，44（11）：1806－1812.

［6］ Dutta N C，OdéH.Attenuation and dispersion of compressional waves in fluid－filled porous rocks with partial gas saturation（White model），Part I：Biot theory.Geophysics，1979，44（11）：1777－1788.

［7］ Johnson D L.Theory of frequency dependent acoustics in patchy－saturated porous media.J.Acoust.Soc.Am.，2001，110（2）：682－694.

［8］ Müller T M，Gurevich B，Lebedev M.Seismic wave attenuation and dispersion resulting from wave－induced flow in porous rocks－A review.Geophysics，2010，75（5）：75A147－75A164.

［9］ Gurevich B，Zyrianov V B，Lopatnikov S L.Seismic attenuation in finely layered porous rocks：Effects of fluid flow and scattering.Geophysics，1997，62（1）：319－324.

［10］ Toms J，Müller T M，Ciz R，et al.Comparative review of theoretical models for elastic wave attenuation and dispersion in partially saturated rocks.Soil Dynamics and Earthquake Engineering，2006，26（6－7）：548－565.

［11］ Dvorkin J，Nur A.Dynamic poroelasticity：A unified model with the Squirt and the Biot mechanisms.Geophysics，1993，58（4）：524－533.

［12］ 聂建新，杨顶辉，杨慧珠.基于非饱和多孔隙介质BISQ模型的储层参数反演.地球物理学报，2004，47（6）：1101－1105.Nie J X，Yang D H，Yang H Z.Inversion of reservoir parameters based on the BISQ model in partially saturated porous media.Chinese J.Geophys.（in Chinese），2004，47（6）：1101－1105.

［13］ Nie J X，Ba J，Yang D H，et al.BISQ model based on a Kelvin－Voigt viscoelastic frame in a partially saturated porous medium.Applied Geophysics，2012，9（2）：213－222.

［14］ 刘炯，马坚伟，杨慧珠.White球状Patchy模型中纵波传播研究.地球物理学报，2010，53（4）：954－962.Liu J，Ma J W，Yang H Z.Research on P－wave＇s propagation in White＇s sphere model with patchy saturation.Chinese J.Geophys.（in Chinese），2010，53（4）：954－962.

［15］ 刘炯，马坚伟，杨慧珠.周期成层Patchy模型中纵波的频散和衰减研究.地球物理学报，2009，52（11）：2879－2885.Liu J，Ma J W，Yang H Z.Research on dispersion and attenuation of P wave in periodic layered－model with patchy saturation.Chinese J.Geophys.（in Chinese），2009，52（11）：2879－2885.

［16］ Pride S R，Berryman J G，Harris J M.Seismic attenuation due to wave－induced flow.J.Geophys.Res.，2004，109：B01201，doi：10.1029／2003JB002639.

［17］ Ba J，Nie J X，Cao H，et al.Mesoscopic fluid flow simulation in double－porosity rocks.Geophys.Res.Lett.，2008，35：L04303，doi：10.1029／2007GL032429.

［18］ Ba J，Cao H，Yao F C，et al.Double－porosity rock model and squirt flow in the laboratory frequency band.Appl.Geophys.，2008，5（4）：261－276.

［19］ 巴晶.双重孔隙介质波传播理论与地震响应实验分析.中国科学G辑，2010，40（11）：1398－1409.Ba J.Wave propagation theory in double－porosity medium and experimental analysis on seismic responses.Scientia Sinica Physica，Mechanica ＆Astronomica（in Chinese），2010，40（11）：1398－1409.

［20］ Ba J，Yang H Z，Xie G Q.AGILD seismic modeling for double－porosity media.Piers Online，2008，4（3）：doi：10.2529／PIERS071107235651.

［21］ Ba J，Carcione J M，Nie J X.Biot－Rayleigh theory of wave propagation in double－porosity media.J.Geohpys.Res.，2011，116：B06202，doi：10.1029／2010JB008185.

［22］ Ba J，Cao H，Yao F C.Velocity dispersion of P－waves in sandstone and carbonate：Double－porosity and local fluid flow theory.SEG Annual Meeting 2010，Denver，US，2010：2557－2563.

［23］ 巴晶，Carcione J M，曹宏等.非饱和岩石中的纵波频散与衰减：双重孔隙介质波传播方程.地球物理学报，2012，55（1）：219－231.Ba J，Carcione J M，Cao H，et al.Velocity dispersion and attenuation of P waves in partially－saturated rocks：Wave propagation equations in double－porosity medium.Chinese J.Geophys.（in Chinese），2012，55（1）：219－231.

［24］ Sun W T，Ba J，Müller T M，et al.P－wave dispersion and attenuation in patchy－saturated Rocks.White，Dutta，Johnson and Biot－Rayleigh theories，The 74th EAGE2012in Copenhagen，2012，Copenhagen，Denmark.

［25］ Berryman J G，Wang H F.The elastic coefficients of doubleporosity models for fluid transport in jointed rock.J.Geophys.Res.，1995，100（B12）：24611－24627.

［26］ Berryman J G，Wang H F.Elastic wave propagation and attenuation in a double－porosity dual－permeability medium.Int.J.Rock Mech.Min.Sci.，2000，37（1－2）：63－78.

［27］ Santos J E，CorberóJ M，Douglas J.Static and dynamic behavior of a porous solid saturated by a two－phase fluid.J.Acoust.Soc.Am.，1990，87（4）：1428－1438.

［28］ Santos J E，Douglas J，CorberóJ M，et al.A model for wave propagation in a porous medium saturated by a two－phase fluid.J.Acoust.Soc.Am.，1990，87（4）：1439－1448.

［29］ 赵海波.不相混气液饱和孔隙介质声场数值模拟与应用研究［博士论文］.北京：中国科学院声学研究所，2007.Zhao H B.Numerical study of acoustic wavefield in porous media saturated with two immiscible fluids and its application［Ph.D.thesis］（in Chinese）.Beijing：Institute of Acoustics，Chinese Academy of Sciences，2007.

［30］ Johnson D L，Koplik J，Dashen R.Theory of dynamic permeability and tortuosity in fluid－saturated porous media.J.Fluid Mech.，1987，176：379－402.

［31］ 唐晓明.含孔隙、裂隙介质弹性波动的统一理论——Biot理论的推广.中国科学（地球科学），2011，41（6）：784－785.Tang X M.A unified theory for elastic wave propagation through porous media containing cracks：An extension of Biot′s poroelastic wave theory.Science China Earth Sciences，2011，54（9）：1441－1452.

［32］ 陈雪莲，唐晓明.孔、裂隙并存地层中的声波测井理论及多极子声场特征.地球物理学报，2012，55（6）：2129－2140.Chen X L，Tang X M.Numerical study on the characteristics of acoustic logging response in the fluid－filled borehole embedded in crack－porous medium.Chinese J.Geophys.（in Chinese），2012，55（6）：2129－2140.

［33］ Rayleigh L.On the pressure developed in a liquid during the collapse of a spherical cavity.Philos.Mag.，1917，34（200）：94－98.

［34］ Xu S Y，White R E.A physical model for shear－wave velocity prediction.Geophysical Prospecting，1995，44（4）：687－717.

［35］ Xu S Y，Payne M A.Modeling elastic properties in carbonate rocks.The Leading Edge，2009，28（1）：66－74.

［36］ Mavko G，Mukerji T，Dvorkin J.The Rock Physics Handbook－Tools for Seismic Analysis of Porous Media（2nd ed）.New York：Cambridge University Press，2009.

［37］ Norris A N.A differential scheme for the effective moduli of composites.Mechanics of Materials，1985，4（1）：1－16.

［38］ Kuster G T，Toksöz M N.Velocity and attenuation of seismic waves in two－phase media：Part I.Theoretical formulations.Geophysics，1974，39（5）：587－606.

［39］ Sams M S，Neep J P，Worthington M H，et al.The measurement of velocity dispersion and frequency－dependent intrinsic attenuation in sedimentary rocks.Geophysics，1997，62（5）：1456－1464.

［40］ 徐光成，巴晶，李劲松等.阿姆河右岸麦捷让地区碳酸盐岩储层流体检测研究.地球物理学进展，2013，28（3），待刊.Xu G C，Ba J，Li J S，et al.A study on fluid detection in Metajan carbonate reservoirs in the right bank block of Amu Darya river.Progress in Geophys.（in Chinese），2013，28（3），in press.

［41］ Adam L，Batzle M，Brevik I.Gassmann′s fluid substitution and shear modulus variability in carbonates at laboratory seismic and ultrasonic frequencies.Geophysics，2006，71（6）：F13－F183.

［42］ Cadoret T，Marion D，Zinszner B.Influence of frequency and fluid distribution on elastic wave velocities in partially saturated limestones.J.Geophys.Res.，1995，100（B6）：9789－9803.

Rock physics model and gas saturation inversion for heterogeneous gas reservoirs

BA Jing1，YAN Xin－Fei1，CHEN Zhi－Yong1，XU Guang－Cheng1，BIAN Cong－Sheng1，CAO Hong1，YAO Feng－Chang1，SUN Wei－Tao2
1 Research Institute of Petroleum Exploration and Development，PetroChina，Beijing100083，China
2 Zhou Pei－Yuan Center for Applied Mathematics，Tsinghua University，Beijing100083，China

In heterogeneous natural gas reservoirs，generally gas forms countless small"patchy"－like packets embedded in the host matrix of water－saturated rocks.This heterogeneity feature（also called the"patchy－saturation"）causes significant velocity dispersion and attenuation phenomena for seismic wave propagation.To build an appropriate rock physics model for the application of fluid identification in carbonate reservoirs，multi－scale theoretical modeling is performed for partially－saturated rocks and the quantitative relations between wave responses in different scales and basic properties of lithology and pore fluids are predicted.This approach of modeling is applied in limestone gas reservoirs of the right bank block of Amu Darya river.A multi－scale rock physics template is presented.Comparisons with experimental data，fine interpretation results of log data and seismic data have proved its validity and applicability.In combination with the methods of post－stack wave－impedance inversion and pre－stack elastic parameter inversion，seismic data is used to estimate rock porosity and gas saturation of the reservoirs.The results of estimate are in good agreement with the production status of the wells.

Rock physics model，Biot－Rayleigh theory，Heterogeneity，Porosity，Saturation，Gas reservoir identification

10.6038／cjg20130527

P631

2012－11－02，2012－12－09收修定稿

国家自然科学基金青年项目（41104066），中国石油勘探开发研究院中青年创新基金项目（2010－A－26－01），中国石油天然气集团公司“十二五”基础研究项目（2011A－3601），国家油气重大专项（2011ZX05004－003）资助.

巴晶，男，1980年生，博士，高级工程师，主要从事岩石物理学理论、孔隙介质声学、地震波场正演与天然气藏检测方面的研究.E－mail：baj04＠mails.tsinghua.edu.cn，baj08＠petrochina.com.cn

巴晶，晏信飞，陈志勇等.非均质天然气藏的岩石物理模型及含气饱和度反演.地球物理学报，2013，56（5）：1696－1706，

10.6038／cjg20130527.

Ba J，Yan X F，Chen Z Y，et al.Rock physics model and gas saturation inversion for heterogeneous gas reservoirs.Chinese J.Geophys.（in Chinese），2013，56（5）：1696－1706，doi：10.6038／cjg20130527.

（本文编辑 胡素芳）