基于碳酸盐岩裂缝岩石物理模型的横波速度和各向异性参数预测

张广智，陈怀震，王 琪，印兴耀

中国石油大学（华东）地球科学与技术学院，青岛 266555

1 引 言

岩石物理模型在地震反演和解释中有着十分重要的作用，是连接地震属性（纵、横波速度等）以及储层参数（孔隙度、饱和度、泥质含量等）的重要纽带［1－4］.正确适用的岩石物理模型不仅能够为正反演提供基础和必要的数据资料，同时可以降低地震解释的风险.

各向异性是沉积岩石中普遍存在的现象［5］.通常把具有水平对称轴，垂直或近似垂直平行排列的碳酸盐岩裂缝储层等效成HTI（Horizontal Transverse Isotropic）介质［6－8］.目前，大量研究表明，地震各向异性是影响地震反射振幅随偏移距变化（AVO）的一个因素，而且裂缝型碳酸盐岩储层的地震反射振幅还会表现出随测线方位角变化（AVOA）的特征.Ruger［9］详细论述了各向异性介质（VTI和HTI）的地震波传播特征的变化，并且依照Thomsen［10］弱各向异性近似理论提出各向异性介质反射系数近似式，为基于各向异性理论的地震反演提供了理论基础.

随着各向异性理论研究的深入，以及砂泥岩岩石物理模型在碳酸盐岩储层中的不适用性，基于各向异性理论的岩石物理模型的研究越来越被关注［11－17］.本文给出碳酸盐岩裂缝储层岩石物理模型的建立步骤，重点研究了依照Hudson［18－19］模型和Schoenberg［20］线性滑动模型在各向同性介质背景中添加裂缝系统，并且利用Brown和Korringa［21］公式完成各向异性岩石的流体替换，计算饱含流体裂缝储层的弹性参数和各向异性参数.同时基于Ruger各向异性反射系数近似式，分析裂缝密度e和缝隙饱和不同流体（饱和油水或饱和气）对反射系数的影响，推导出不同流体充填情况下地震反射系数与裂缝密度e的关系式.

2 方法原理

碳酸盐岩基质主要由方解石和白云石组成，其次考虑含泥质和砂质时的影响；孔隙主要由粒间孔隙（含溶孔）、溶洞和裂缝三部分组成，本文主要讨论裂缝的作用；孔隙流体由油、气和水组成（图1）.

图1 裂缝型碳酸盐岩岩石物理模型示意图Fig.1 Fractured carbonate rock physics model

本文提出裂缝型碳酸盐岩岩石物理模型的构建流程如下：

（1）利用Voigt－Reuss－Hill平均计算混合矿物的弹性模量；

（2）利用DEM模型将孔隙加进系统，并计算干燥岩石骨架的体积模量和剪切模量；

（3）利用Hudson理论和Schoenberg ＆Sayers理论，在碳酸盐岩介质各向同性背景中加入裂缝系统，修正计算出的模量；

（4）利用Wood公式将孔隙流体进行混合，计算出混合流体的体积模量；

（5）利用Brown和Korringna公式完成缝隙流体替换；

（6）计算裂缝型碳酸盐岩的弹性参数和各向异性参数.

裂缝型碳酸盐岩岩石物理模型构建的基本思想是：在各向同性背景介质的基础上添加裂缝的影响，计算干岩石刚度系数矩阵，依照各向异性流体替换方法估算得到饱含流体岩石的弹性参数和各向异性参数.裂缝型碳酸盐岩岩石物理模型建立的部分步骤解析如下.

2.1 VRH矿物平均

利用Voigt－Reuss－Hill平均计算混合矿物的弹性模量：

2.2 裂缝模型

目前有两种应用广泛的裂缝模型，Hudson模型和Schoenberg线性滑动模型.

Hudson理论是建立在整体平均的基础上［22］.该模型假设弹性介质的内部分布着薄硬币形状的椭球缝隙（图2）.

Hudson模型利用裂缝密度和缝隙纵横比来描述裂缝系统的结构.裂缝密度e的定义如下：

图2 Hudson微小裂隙模型Fig.2 Hudson′s penny－shaped crack model

K′和μ′是缝隙中充填介质的体积模量和剪切模量，λ和μ是不含裂隙岩石的Lame参数.

（1）当缝隙为湿裂缝（饱含油水），且缝隙纵横比α≪0.1时，［K′＋（4／3）μ′］／（μα）≫1：

Schoenberg线性滑动模型是基于Backus［23］平均提出的（图3）.

对于一组可以旋转对称的裂缝系统，Schoenberg模型的弹性矩阵由各向同性参数λ和μ，以及垂直于裂缝面和平行于裂缝面的弹性差值ΔN和ΔT进行描述［24］，表示裂缝对骨架岩石各向同性特征的影响.Schoenberg线性滑动模型的弹性矩阵为：

图4 ΔN和ΔT随VP／VS的变化关系Fig.4 ΔN和ΔTvariation with VP／VS

同时讨论缝隙饱含气时Thomsen参数与裂缝密度之间的关系（图6）：

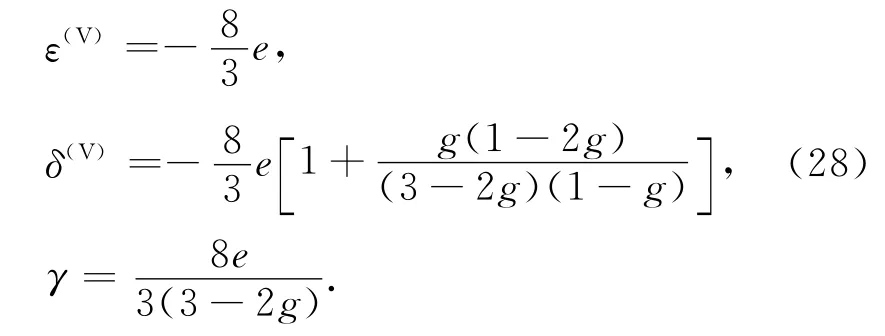
从图6中可以看出，缝隙中饱含气时，三个各向异性参数的绝对值都随着裂缝密度的增加而增大.

综上，结合式（27）和式（28），讨论干裂缝（饱含气）和湿裂缝（饱含油水）时，Thomsen参数ε（V），δ（V）和γ与横纵波速比的关系（图7）.

图7表明，缝隙中所含流体的不同会引起ε（V）和δ（V）随横纵波速比的变化特征发生改变，而γ并不受缝隙中流体的影响.当缝隙含油水时ε（V）数值为0，含气时ε（V）会变为负值；当缝隙中含油水时δ（V）数值随横纵波速比变化剧烈，而缝隙含气时δ（V）随横纵波速比变化不明显.因此可根据该特征来识别裂缝储层流体的特性.

2.3 裂缝模型流体替换

为进一步完善介质流体替换理论，Gassmann［29］提出各向异性孔隙岩石的流体替换公式，其线性弹性系数矩阵表示如下：

图7 干裂缝和湿裂缝Thomsen参数随VS／VP变化Fig.7 Dry fracture and wet fracture′s Thomsen parameters variation with VS／VP

Gassmann方程假设矿物是均质和各向同性的，尽管干岩石和饱和岩石具有任意各向异性特征.Brown和Korringa对各向异性岩石的流体替换进行了研究，虽然计算结果与Gassmann方程相似，但Brown和Korringa流体替换的前提是假设矿物为各向异性的.

3 流体充填裂缝介质反射系数

基于Ruger的HTI介质纵波反射系数，讨论当缝隙中充填不同流体时纵波反射系数与裂缝密度e的关系.

（2）当缝隙中含气时，将式（28）代入式（35）得含气时纵波反射系数为：

其中，Δe＝e2－e1，e1和e2分别指裂缝介质上下分层的裂缝密度值.

4 应用分析

选取某碳酸盐岩工区的A井为例，对碳酸盐岩裂缝储层岩石物理模型的建立流程进行验证，计算纵、横波速度与测井数据进行对比，提取裂缝储层的Thomsen参数，并分析其各向异性程度.

从图8a—8b中可以看出，通过各向异性岩石物理模型计算的纵波速度和横波速度与测井所得结果相差不大，说明提出的裂缝型碳酸盐岩岩石物理模型构建流程符合要求.图8c为预测的Thomsen参数，Thomsen参数绝对值越大说明介质的各向异性程度越强.

图8中虚线框所标注的位置纵横波速度要小于临近地层的纵横波速度，而且Thomsen各向异性参数的数值变化明显，且Thomsen参数绝对值明显高于其它层段，同时参照测井解释信息，可以说明图中所标注位置为裂缝发育层段.

图8 利用裂缝岩石物理模型估算弹性参数和各向异性参数（a）纵波速度估算与测井数据对比，红色为估算值，蓝色为测井数据；（b）横波速度估算与测井数据对比，红色为估算值，蓝色为测井数据；（c）Thomsen参数估算值（γ（V）＝－γ）.Fig.8 Elastic parameters and anisotropic parameters estimated using fracture rock physics model（a）P wave velocity estimation result comparison with log data，the red line is estimation result，the blue one is logging data；（b）S wave velocity estimation result comparison with log data，the red line is estimation result，the blue one is logging data；（c）Thomsen parameters estimation result（γ（V）＝－γ）.

5 结 论

本文提出了裂缝型碳酸盐岩岩石物理模型的建立步骤.重点分析了如何在碳酸盐岩岩石骨架中利用Hudson模型和Schoenberg模型引入裂缝系统，以及Thomsen参数、流体指示因子随裂缝密度e、横纵波速比和缝隙饱含流体的变化特征.

选取碳酸盐岩工区A井进行横波速度和各向异性参数的估算，横波速度的估算结果与测井结果相差不大，且各向异性参数能够较好地反映裂缝发育位置，说明基于碳酸盐岩裂缝岩石物理模型进行横波和各向异性参数估算的可靠性.

由于碳酸盐岩裂缝储层的复杂性，为了更逼近地下介质的真实特征，考虑将基质中添加泥质，以及缝隙中充填方解石的条件进行横波和各向异性参数估算，为地震叠前反演工作提供更加适用的岩石物理资料.

（

）

［1］ 镇晶晶，刘洋.裂缝介质岩石物理模型研究综述.地球物理学进展，2011，26（5）：1708－1716.

Zhen J J，Liu Y.Review over physical model of fractured rock medium.ProgressinGeophys.（in Chinese），2011，26（5）：1708－1716.

［2］ 蒋炼，文晓涛，贺振华等.礁滩储层内部孔隙结构模型模拟与孔隙度预测.地球物理学报，2011，54（6）：1624－1633.

Jiang L，Wen X T，He Z H，et al.Pore structure model simulation and porosity prediction in reef－flat reservoir.ChineseJ.Geophys.（in Chinese），2011，54（6）：1624－1633.

［3］ 马淑芳，韩大匡，甘利灯等.地震岩石物理模型综述.地球物理学进展，2010，25（2）：460－471.

Ma S F，Han D K，Gan L D，et al.A review of seismic rock physics models.ProgressinGeophys.（in Chinese），2010，25（2）：460－471.

［4］ 徐胜峰，李勇根，曹宏.地震岩石物理研究概述.地球物理学进展，2009，24（2）：680－691.

Xu S F，Li Y G，Cao H.A review of seismic rock physics.ProgressinGeophys.（in Chinese），2009，24（2）：680－691.

［5］ 吴国忱.各向异性介质地震波传播与成像.山东东营：中国石油大学出版社，2006：1－3.

Wu G C.Propagation and Imaging for Seismic Wave in Anisotropic Media（in Chinese）.Shandong Dongying：Press of China University of Petroleum，2006：1－3.

［6］ 杜启振，杨慧珠.方位各向异性介质的裂缝预测方法研究.中国石油大学学报（自然科学版），2003，27（4）：32－36.

Du Q Z，Yang H Z.Detection method for fractures in azimuthally anisotropic media.JournalofChinaUniversity ofPetroleum（EditionofNaturalScience）（in Chinese），2003，27（4）：32－36.

［7］ 李录明，罗省贤，王明春等.各向异性介质三维纵横波联合叠前反演方法及应用.石油地球物理勘探，2010，45（1）：60－65.

Li L M，Luo S X，Wang M C，et al.3DPP－PS joint inversion method and application in anisotropic medium.Oil GeophysicalProspecting（in Chinese），2010，45（1）：60－65.

［8］ 肖鹏飞，王世星，曲寿利等.倾角对裂缝密度反演的影响分析.石油物探，2009，48（6）：544－551.

Xiao P F，Wang S X，Qu S L，et al.Analysis on the impact of dip on fracture density inversion.GeophysicalProspecting forPetroleum（in Chinese），2009，48（6）：544－551.

［9］ Ruger A.Reflection coefficient and azimuthal AVO analysis in anisotropic media［Ph.D.thesis］.Colorado：Colorado School of Mines，1996.

［10］ Thomsen L.Weak elastic anisotropy.Geophysics，1986，51（10）：1954－1966.

［11］ 李磊，郝重涛.横向各向同性介质和斜方介质各向异性参数的约束条件.地球物理学报，2011，54（11）：2819－2830.

Li L，Hao C T.Constraints on anisotropic parameters in transversely isotropic media and the extensions to orthorhombic media.ChineseJ.Geophys.（in Chinese），2011，54（11）：2819－2830.

［12］ 杜启振，孔丽云，韩世春.裂缝诱导各向异性双孔隙介质波场传播特征.地球物理学报，2009，52（4）：1049－1058.

Du Q Z，Kong L Y，Han S C.Wavefield propagation characteristics in the fracture－induced anisotropic doubleporosity medium.ChineseJ.Geophys.（in Chinese），2009，52（4）：1049－1058.

［13］ 阴可，杨慧珠.各向异性介质中的AVO.地球物理学报，1998，41（3）：382－390.

Yin K，Yang H Z.AVO in anisotropic media.ChineseJ.Geophys.（in Chinese），1998，41（3）：382－390.

［14］ 梁锴，印兴耀，吴国忱.TTI介质qP波入射精确和近似反射透射系数.地球物理学报，2011，54（1）：208－217.

Liang K，Yin X Y，Wu G C.Exact and approximate reflection and transmission coefficient for incident qP wave in TTI media.ChineseJ.Geophys.（in Chinese），2011，54（1）：208－217.

［15］ 张广智，郑静静，印兴耀.基于Curvelet变换的多尺度性识别裂缝发育带.石油地球物理勘探，2011，46（5）：757－762.

Zhang G Z，Zheng J J，Yin X Y.Identification technology of fracture zone and its strike based on the Curvelet transform.OilGeophysicalProspecting（in Chinese），2011，46（5）：757－762.

［16］ 李爱山，印兴耀，张繁昌等.VTI介质中的弹性阻抗与参数提取.地球物理学进展，2008，23（6）：1878－1885.

Li A S，Yin X Y，Zhang F C，et al.Elastic impedance in VTI media and parameter extraction.ProgressinGeophys.（in Chinese），2008，23（6）：1878－1885.

［17］ 齐宇，魏建新，狄帮让等.横向各向同性介质纵波方位各向异性物理模型研究.石油地球物理勘探，2009，44（6）：671－674.

Qi Y，Wei J X，Di B R，et al.Compressional wave（P－wave）azimuthal anisotropy physical model studies in transversally isotropic medium.OilGeophysicalProspecting（in Chinese），2009，44（6）：671－674.

［18］ Hudson J A.Overall properties of a cracked solid.MathematicalProceedingsoftheCambridgePhilosophical Society，1975，88（2）：371－384.

［19］ Hudson J A.Wave speeds and attenuation of elastic waves in material containing cracks.GeophysicalJournalofthe RoyalAstronomicalSociety，1981，64（1）：133－150.

［20］ Schoenberg M.Elastic wave behavior across linear slip interfaces.J.Acoust.Soc.Amer.，1980，68（5）：1516－1521.

［21］ Brown R J，Korringa J.On the dependence of the elastic properties of a porous rock on the compressibility of the pore fluid.Geophysics，1975，40（4）：608－616.

［22］ Sava D.Quantitative data integration for fracture characterization using statistical rock physics［Ph.D.thesis］.California：Stanford University，2004.

［23］ Backus G E.Long－wave elastic anisotropy produced by horizontal layering.J.Geophys.Res.，1962，67（11）：4427－4440.

［24］ Schoenberg M，Muir F.A calculus for finely layered anisotropic media.Geophysics，1989，54（5）：581－589.

［25］ Schoenberg M，Douma J.Elastic wave propagation in media with parallel fractures and aligned cracks.Geophys.Prospect.，1988，36（6）：571－590.

［26］ Schoenberg M，Protazio J.‘Zoeppritz’rationalized and generalized to anisotropy.SeismicExplor.，1992，1：125－144.

［27］ Schoeberg M，Sayers C M.Seismic anisotropy of fractured rock.Geophysics，1995，60（1）：204－211.

［28］ Bakulin A，Grechka V，Tsvankin I.Estimation of fracture parameters from reflection seismic data－Part I：HTI model due to a single fracture set.Geophysics，2000，65（6）：1788－1802.

［29］ Gassmann F.Uber die elastizitat poroser medien.Vier.der Natur.GesellschaftZurich，1951，96（1）：1－23.

［30］ Bachrach R，Sengupta M，Salama A，et al.Reconstruction of the layer anisotropic elastic parameters and high resolution fracture characterization from P－wave data：a case study using seismic inversion and Bayesian rock physics parameter estimation.Geophys.Prospect.，2009，57（2）：253－262.