S-meso紧空间

杨思鑫， 幸华雄

(成都理工大学 管理科学学院， 四川 成都 610059)

1 预备知识

Levine在文献[1]中首次引入拓扑空间中半开集的概念并且对其性质进行了研究，自此半开集的概念及其性质引起了一些拓扑学者的关注，成为拓扑学讨论的重要内容之一，一些由半开集定义而得到的空间,如可数S-闭空间、S-闭空间、S-可膨胀空间等被定义.2006年，文献[2]中定义了S-仿紧空间，并对S-仿紧空间的性质进行了研究.本文将在此基础上，给出新的更为复杂的空间——S-meso紧空间，对其定义并对其性质进行初步研究.

本文中研究的空间默认为不满足分离性公理的拓扑空间，除非有特殊说明.设(X,T)是一个拓扑空间，A是X的一个子集，则A的闭包，A的内部,(X,T)在A上的相对拓扑，分别记为cl(A), int(A),TA.

定义1设空间(X,T)中的一个子集记为A，A称为(X,T)的一个半开集[1]，假设存在X的一个开集U，使U⊆A⊆cl(U)等价的说法是A⊆cl(int(A)).半开集的补集称为半闭集[3].用scl(A)来表示A的半闭包[4]：包含A的最小的半闭集.

定义2[5]设A是空间(X,T)中的一个子集，A称为的一个正则开，如果A=int(cl(A))；A称为正则闭，如果A=cl(int(A))；A称为预开，如果A=int(cl(A))；

为论证方便，本文有以下约定：

(1)SO(X, T)表示(X, T)中X的半开集族；

(2)RO(X, T)表示(X, T)中X的正则开集族；

(3)RC(X, T)表示(X, T)中X的正则闭集族；

(4)PO(X, T)表示(X, T)中X的预开集族.

对于空间(X, T)，RO(X, T)是拓扑TS的基且TS⊆T，则空间(X,TS)称为(X, T)中半正则的空间.

定义3[6]空间X中的集族记为V称为紧有限，如果X的任意紧集K与V相交仅有有限个元素.

定义4空间X的集族记为V称为S-紧有限的，如果X中的每一个半开的紧子集K仅与V中有限个元相交.

引理1[7]集族F={Fα∶α∈I}是由空间(X,T)的子集构成的：

(a)F是S-紧有限当且仅当{scl(F):α∈I}是S-紧有限

(b)如果F是S-紧有限，则∪α∈Iscl(Fα)=scl(∪α∈IFα)

显然集族F={Fα∶α∈I}是空间(X,T)的

子集是紧有限的当且仅当集族{scl(F)∶α∈I}是紧有限的.

定义5[8]空间(X, T)称为S-闭空间(可数S-闭空间),如果对X任意一个半开覆盖(可数半开覆盖)U都存在一个有限子族V,使子族中元素V的闭包cl(V)覆盖X.

定义6空间(X,T)称为极不连通(简称e.d.)的，如果任意一个开集U的闭包cl(U)在(X,T)中是开集.

定义7[9]空间(X, T)称为meso紧的，若X的任意开覆V存在紧有限的开加细覆盖U.

定义8空间X称为S-meso 紧空间，若X的任意开覆盖V具有紧有限的半开的加细覆盖U.

例如：取X=R是一个实数集，有拓扑空间T={X,Φ,{1}}，则空间(X,T)便是S-meso紧空间.

引理2[7]如果(X, T)是极不连通的，则有scl(U)=cl(U)，其中U∈SO(X,T).

引理3[10]设空间(X, T)的一个子集A，则A∈PO(X, T) 与scl(A)=int(cl(A))互为充要条件.

2 主要结果

定理1如果(X, T)是一个S-meso紧T2空间，则对X中的每一个闭子集A和一点x(x不属于A),存在U∈T且V∈SO(X,T)得x∈U，A⊆V且U∩V=Φ,等价于对X中的一个开集U使x∈U，存在V∈T，则x∈V⊆scl(V)⊆U.

证明对任意y∈A,选一个开集Wy，即y∈Wy且x∉cl(Wy)，所以集族W={Wy∶y∈A}∪{X-A}是X的一个开覆盖，所以W有一个紧有限的半开加细覆盖H ，

取V=∪{cl(H)∶H∈H，且x∩H≠Φ即V是一个包含A的半开集，又因为cl(V)=∪{cl(H)∶H∈H且x∩H≠Φ,因此U=X-cl(V)是一个包含x的开集，所以U∩V=Φ得证.

推论1每一个S-meso紧T2空间是半正则的，即T=TS.

证明空间(X, T)是S-meso紧T2空间，由定理1，空间中任意x∈U∈T ，存在V∈T有x∈V⊆scl(V)⊆U；另因为V⊆int(cl(V))，则A∈PO(X, T).由引理3 scl(A)=int(cl(A))，得出x∈V⊆int(cl(V)) ⊆U，所以正则开集族V={int(cl(V)):V∈T}是空间(X,T)的一个基，即T= Ts.

推论2每一个极不连通的S-meso紧T2空间是正则的.

证明由引理2知极不连通空间(X,T)中半开集V，满足scl(V)=cl(V)，又由定理1，对于空间中一点x，x∈U,存在V∈T有x∈V⊆scl(V)⊆U，综上得cl(V)⊆U.所以是正则空间得证.

定理2设(X,T)是一个正则空间且为极不连通的，如果任意X的开覆盖都存在一个S-紧有限的半开加细，则X的任意开覆盖都存在一个紧有限开加细.

证明取X的一个开覆盖U，对任意一个x∈X取Ux∈U，根据正则性，开集Vx∈T 且x∈VX⊆cl(Vx)⊆Ux,则V={Vx∶x∈X}是X的一个开覆盖，则V有一个S-紧有限半开加细覆盖W={Wβ∶β∈B}.

任意的β∈B，取Hβ使满足Hβ⊆Wβ⊆cl(Hβ),又因为对任意的β∈B，cl(Hβ)=cl(Wβ)⊆(Vx)(Vx∈V)和cl(H)⊆U(U∈U).因为(X, T)是极不连通的，所以cl(Hβ)∈T(β∈B).

下面证集族H={cl(Hβ)∶β∈B}是紧有限的.

由W={Wβ∶β∈B}是S-紧有限，则任意半开紧集K⊂X，K与W中有限元相交.定义4和定义3显然得到H={cl(Hβ)∶β∈B}是紧有限.

推论3每一个极不连通的S-meso紧T2空间是meso紧空间.

证明由meso紧空间定义和定理2显然得到.

定理3在每一个可数S-闭空间中，S-紧有限集中由半开集构成的集族是有限的.

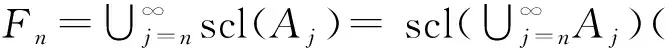
再证∩{int(cl(Fn))∶n∈N}=Φ

假设，存在t∈{int(cl(Fn)}∶n∈N}对每一个n∈N，Vn(t)∈T，则t∈Vn(t)⊆cl(Fn) 但是因为A是S-紧有限的，所以存在紧集Mt，Mt∈SO(X,T),Mt与A 有有限交.现在选取Ut⊆Mt⊆cl(Ut) 那么Unt∩Ut≠Φ对每一个n∈N,存在Sn∈Vn(t)∩Ut⊆cl(Fn)∩Vt，因此Ut∩Fn≠Φ进而，Fn∩Mn≠Φ即Mt与A相交有有限元，所以上面的假设不成立，∩{int(cl(Fn))∶n∈N}=Φ正确.定理证毕.

推论4每一个S-meso紧可数S-闭空间是紧空间.

证明因为每一个紧的e.d.空间是S-闭空间，结合定理3有关内容，本推论易得.

推论5取(X,T)是极不连通空间，则下面(a)(b)等价

(a)(X,T)是S-meso紧也是S-闭空间.

(b)(X,T)是紧空间.

[1] Levine N.Semi-open sets and semi-continuity in topological spaces[J]. Amesr. Math.Monthly,1963,70:36-41.

[2] AL-zoubi K Y.S-paracompact[J].Acta Math. Hungar， 2006, 110 (1-2)：165-174.

[3] Crossely S G.Semi-closed and semi-continuity in topological spaces[J]. Texas J. Sci,1971,22:123-126.

[4] 王国俊.半闭空间的性质[J],数学学报, 1981,24(1):55-63.

[5] 周艳红，付传秀.局部meso紧空间[J].湖北民族学院学报:自然科学版，2007,25(2):155-157.

[6] 高国士.拓扑空间论[M].北京:科学出版社，2000.

[7] AL-zoubi K Y.S-expandable spaces[J].Acta Math. Hungar, 2004, 102 (1-2):203-212.

[8] Thompson T. S-closed spaces[J]. Proc. Amer. Math. Soc.,1976,60,335-338.

[9] 王建军，朱培勇.meso-紧空间的可数乘积[J].纯粹数学与应用数学,2011,27(2):261-266.

[10] Jankovic D S. A note onmappings of extremally disconnected spaces[J]. Acta Math.Hungar.,1985,46,83-92.