WSNS中基于Fusion－Bayes的离群点检测

徐苏娅，胡彩平，王立松

(南京航空航天大学计算机科学与技术学院，江苏南京 210016)

无线传感器网络(Wireless Sensor Networks，WSN)由部署在监测区域内大量的廉价微型传感器节点组成，通过无线通信的方式形成一个多跳的自组织网络系统，其目的是协作的感知、采集和处理网络覆盖的地理区域中感知对象的信息，并发给用户［1］。无线通信等技术的快速发展，推动了低功耗多功能传感器的快速发展，从而使这种网络系统的应用越来越广泛，包括环境监测、交通管理、医疗卫生、工农业等。然而由于无线传感器网络自身存在的一些缺陷以及采集数据量越来越大等因素的影响，采集的数据样本中不可避免地存在一些错误或异常数据，即所谓的离群点。在现实社会中，相对于那些经常发生和出现的事物，人们往往对那些不常出现的特别事件或物体更感兴趣［2］。例如对于森林检测而言，温度异常的数据或许预示火灾的发生，因此对离群点的检测是有必要的。

到目前为止，对离群点还没有一个正式的定义。Hawkins是这样定义离群点的:“如果在一个数据样本与其他样本之间存在足以引起怀疑的差异，则称其为离群点［3］。”离群点有多种别名:孤立点、异常点、新颖点、偏离点、噪音等。在许多研究中，为减少不一致数据也即离群数据对分析结果的影响，离群点常被忽略或者作为噪声被处理，然而一个人的噪声可能是另一个人的信号，不加分析的舍弃离群数据，可能导致重要信息的丢失。例如在欺诈检测中，离群数据可能意味着欺诈行为的发生;在环境监测中，离群数据可能预示着灾害天气的到来。

根据离群点的定义，当一个数据样本的属性值有异常时，它会被识别为离群点。相对于多属性的数据样本来说，单个属性的数据样本更容易被识别。然而，每个传感器节点都配备多个不同的传感器，这样数据样本就存在多个属性，这些属性可能就存在特定的相关性。因此，把多个数值属性融合之后再进行离群点检测，其正确性会更高，也更具有实际意义。

1 相关工作

1.1 数据融合知识

数据融合最早起源于军事领域，是一个愈来愈受到人们重视的研究方向。它的诞生可以归结于在一个系统中使用了多个不同的传感器，因此也称为多传感器数据融合。目前对数据融合还没有得到一致的定义，它是针对使用多个或多类传感器系统的处理方法，利用计算机和嵌入式技术对按时间序列获得的数据信息在一定规则下做出决策和估计。

数据融合的关键技术主要是数据转换、数据相关、数据库和融合计算等，其中融合计算是多传感器数据融合系统的核心技术［4］。文中用到了数据转换技术，由于多传感器输出的数据形式、环境描述不一样，数据融合中心处理这些不同来源的信息时，首先需要把这些数据转换成相同的形式和描述，然后再进行相关处理。数据转换时，不仅要转换不同层次的信息，而且需要转换对环境或目标描述的不同与相似之处。即使同一层次的信息，也存在不同的描述。再者，数据融合存在时间性与空间性，因此要用到坐标变换。坐标变换的非线性带来的误差直接影响数据的质量和时空校准，影响融合处理的质量［5－6］。

1.2 贝叶斯分类

贝叶斯的主要思想是这样的:对于给出的待分类项，求解在此项出现的条件下各个类别出现的概率，哪个最大就认为此待分项就属于哪个类别。贝叶斯分类是一类分类算法的总称，这类算法是以贝叶斯定理为基础的，故统称为贝叶斯分类。贝叶斯定理也称为贝叶斯推理，是18世纪英国学者贝叶斯根据条件概率提出的。假设表示事件B已经发生的前提下，事件A发生的概率，叫作事件B发生下事件A的条件概率。贝叶斯定理基本公式为p(B)/P(A)。

贝叶斯分类的正式定义如下:假设有一个未知数据样本x{a1，a2，…，am}，属性个数为m，其中每个a为x的一个特征属性，假设数据类别为n，集合C={y1，y2，…，yn}，已知数据样本，分别计算，如果概率最大，即，那么该数据样本属于第 k 类，即 x∈yk［7－8］。

本文利用贝叶斯分类原理，推广到多传感器网络中，将数据分为正常数据和异常数据两个类别，通过对部分数据训练得到分类模型，然后利用该模型对未知数据进行检测，属于异常数据类别的数据样本就可以认为是离群点。

2 基于数据融合的贝叶斯检测方法

2.1 数据预处理

首先将多传感器收集的多属性数据进行数据转换，使数值属性都变成纯量数据，这样就可以将多维数据进行比较。目前常用的数据转换主要有min－max标准化、log函数转换、atan函数转换、z－score标准化等。

min－max标准化(Min－max normalization)，也叫离差标准化，是对原始数据的线性变化，使结果落到［0，1］区间，转换函数为 x*=(x－min)/(max－min)，其中max为样本数据的最大值，min为样本数据的最小值。这种方法有一个缺陷就是当有新数据加入时，可能导致max和min的变化，因此需要重新定义。log转换函数为x*=log10(x)/log10(max)，其中max为样本数据最大值，并且所有的数据均≥1。atan函数转换利用反正切函数也可以实现数据转换，使用这个方法进行数据转换时要求数据≥0，＜0的数据将被映射到［－1，0］区间上，具体转换方法为 x*=a tan(x)*2/π，其中函数a tan(x)是求x的反正切函数。z－score标准化(zero－mean normalization)，也叫标准差标准化，经过处理的数据符合标准正态分布，即均值为0，标准差为1，其转化函数为x*=(x－u)/σ，其中u为所有样本数据的均值，σ为所有样本数据的标准差。

本文选用的是min－max标准化转换函数，这是比较常用的转换函数，也是最容易实现的函数。通过标准化转换，所有的数据属性都变成无量纲数据，彼此间可以进行融合计算。

2.2 贝叶斯方法检测

假设在无线传感器网络中，每个数据样本用一个n维特征向量表示，这n维特征向量分别用A1，A2，…，An表示。假定数据样本共有m个类，给定一个未知类别的数据样本X，在已知该数据样本的条件下，分类器将预测其属于最高后验概率的类。也就是说，朴素贝叶斯分类将未知样本分配给Ci(1≤i≤m)类当且仅当，对任意的 j=1，2，…，m，j≠i。这样最大的类Ci就被称为最大后验假定，可以根据贝叶斯定理p(Ci)/p(X)求出。

由于对于所有类为常数，只要p(X Ci)P(Ci)最大即可。如果类Ci的先验概率未知，则通常假定这些类是等概率的，即p(C1)=p(C2)=…=p(Cm)，因此问题就转换为对的最大化。否则，就需要最大化，这里类的先验概率可以用公式p(Ci)=si/S计算，其中si是类Ci中的训练样本数，而S是训练样本总数。

多属性数据集的计算开销可能较大，为降低计算开销，可以做类条件独立的朴素假定。给定样本的类标号，假定属性相互条件独立，即在属性间不存在依赖关系。这样

。对未知样本分类，也就是对每个类别Ci，计算的大小。如果，那么数据样本X就被指派到类别 Ci，即数据样本 X被指派到最大的类。

利用数据融合和贝叶斯分类结合的方法进行离群点检测，首先将传感器收集的数据转换成同一样式，然后对不同属性进行融合分类，检测出离群点，分别对所有单个属性、部分属性、所有属性融合检测，分别得出其检测的正确性，并进行比较，实验得出多属性的融合检测结果比单一或低维属性的融合检测效果更好。

2.3 Fusion－Bayesian算法步骤

数据预处理阶段:(1)加载数据样本S，选取温度、湿度、亮度和电压4个属性。(2)利用min－max标准化方法对数据样本S进行标准化处理，使其都变成纯量纲数值。(3)在得到的标准化数据样本中随机插入离群数据样本So。(4)将含有离群点的数据样本分成两部分，一部分是用于训练建模的训练样本Strain;另一部分是用于测试数据的测试样本Stest。训练数据样本阶段:(1)将样本所属类别分为Cnormal和 Coutlier两类，分别求出两类的概率 Pnormal和Poutlier。(2)对指定的类别和数据样本的不同属性融合，分别求出均值mu和方差xigma。

测试数据样本阶段:(1)给定测试样本X，分别计算数据属性xi属于类Ci的概率(2)对于0≤i≤n，其中n为测试样本总数，数据样本X被指派到最大的类中。(3)最后，计算分类的正确率。

2.4 算法复杂度分析

利用数据融合和贝叶斯分类结合的方法进行离群点检测，首先将传感器收集的数据转换成同一样式，然后对不同属性进行融合分类。假设m为数据样本个数，n为数据样本的维度;k为离群点个数;t为将数据样本分成的种类数。在预处理阶段数据标准化的复杂度为O(mn)，随机插入离群数据样本的复杂度为O(k)，训练数据样本阶段的复杂度为O(tm)，测试数据样本阶段的复杂度为O(mnt)。由此可见，Fusion－Bayes算法的复杂度较低，效率较高。

3 实验结果

实验采用的数据样本是由伯克利实验室配置的无线传感器网络收集而来［5］。实验中选取如图1所示的邻近7个传感器节点的数据进行检测，实验在Matlab2007上进行的。每个数据样本有8个属性，即日期、时间、时间戳、标记号、温度、湿度、亮度和电压，实验中选取后4个属性进行融合检测。实验中选取圆圈内标注的簇节点的数据进行实验，Node35是中心节点，其余节点是邻居节点。这些数据样本是传感器节点在2004年3月5日内收集的，在每个传感器节点收集的数据中加入由Matlab随机生成的200个离群点，这些随机生成的离群点和传感器数据样本转换后的格式一致。

图1 伯克利实验布置的传感器分布图

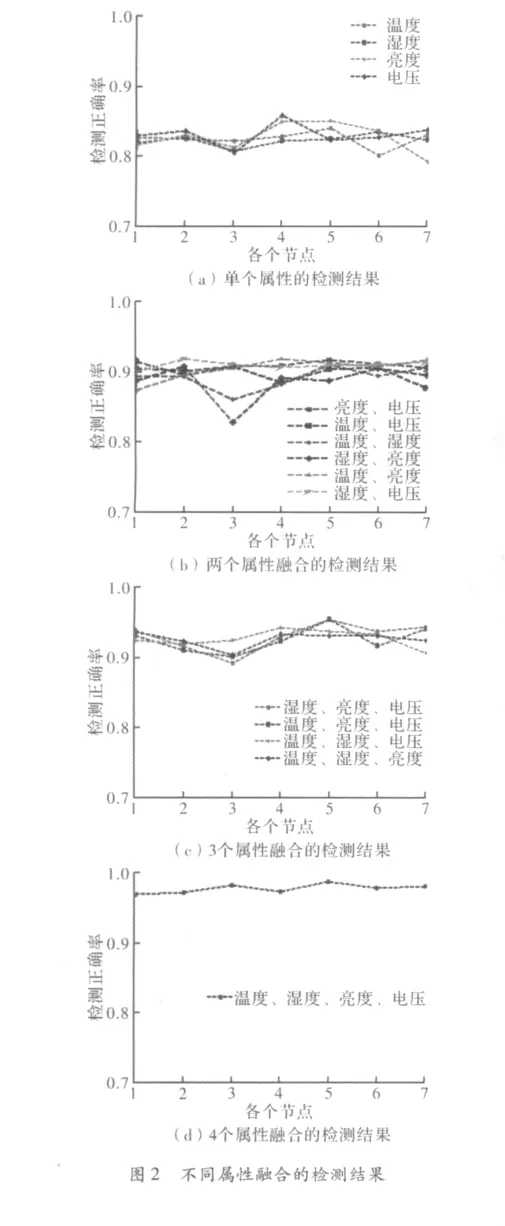
实验中共对7个传感器节点在一天内收集的样本数据进行检测，传感器节点平均31 s进行一次数据记录，每个传感器收集的数据样本融合由Matlab随机生成的离群点，总个数约为2 000个，利用基于数据融合的离群点进行检测，每个数据样本有4个属性，即温度、湿度、亮度和电压，根据不同属性进行融合可得到15组不同的组合，分别对这些组合进行离群点检测实验，每个传感器节点在不同属性融合的前提下，检测正确率如图2所示，其中横坐标对应所选取的7个传感器位置，纵坐标是检测的正确率。

图2可以看出对温度、湿度、亮度和电压4个属性进行融合后检测的正确率最高，仅对单一属性检测的结果最差，选取若干个属性进行融合后再进行离群点检测的正确性居于上述情况之间。但并非是对所有单维属性或低维属性的检测结果都不好，这正是后期需要研究的工作。因为本实验主要是从检测的正确率来考虑，实际应用中还应该考虑时间空间复杂度等其他客观因素的影响，如果能找到一种数据融合模型，在给定的特定条件下，能决定选取几个属性、哪几个属性的融合可以使检测结果最好，那么这将为多属性数据样本的离群点检测工作带来较大的便利，也避免了对所有属性融合和大的计算开销。

4 结束语

提出了基于Fusion－Bayes的贝叶斯检测方法，该方法首先利用数据融合方法对数据样本的多维属性进行数据转换，然后融合不同属性进行离群点检测，相比于单维属性的检测，多维属性融合的检测结果正确性更高。该方法仍存在需要改进的地方，例如在什么情况下可以根据单维或低维属性进行离群点检测，若可以用低维属性进行检测，那么如何选取属性等问题。本文采用的离群点检测方法是贝叶斯方法，虽然贝叶斯方法的检测正确率较高，但是贝叶斯方法设定了过多假设，这些问题在以后的工作中会继续研究，以期找到更好的检测方法。

［1］孙利民，李建中，陈渝，等.无线传感器网络［M］.北京:清华大学出版社，2005.

［2］TAN P N，STEINBACH M，KUMAR V.Introduction to data mining［M］.Beijing:Posts＆ Telecom Press，2006.

［3］HAN J，KAMBER M.Data mining:concepts and techniques［M］.San Francisco:Morgan Kaufmann Publishers，2001.

［4］龚元明，萧德云，王俊杰.多传感器数据融合技术:上［J］.冶金自动化，2002(4):4－7.

［5］那彦，田军，杨万海，等.数据融合技术与多传感器探测［J］.电子科技，2002(3):39 －41.

［6］蔡科，左宪章，康健，等.无线传感器网络测试系统数据融合研究［J］.计算机仿真，2010(7):1－4.

［7］毛晓明，卢光跃，赵国.一种提高无线传感器网络节点定位精度的算法［J］.西安邮电学院学报，2012，17(1):42－46.

［8］石红丽，王洁，唐艳，等.基于无线传感器网络的K均值算法研究［J］.电子设计工程，2011，19(6):113－115.