大射电望远镜巨型柔性并联机构悬索分析及简化*
2013-12-16朱文白唐晓强
黄 亮,朱文白,唐晓强
(1. 中国科学院国家天文台,北京 100012;2. 清华大学精密仪器与机械学系,北京 100084)
20世纪90年代,中国科学家提出利用贵州天然的喀斯特洼地,建造目前世界上最大的单口径射电望远镜——500 m口径球面天文望远镜(Five-hundred-meter Aperture Spherical Telescope, FAST)[1]。FAST包括馈源支撑、主动反射面、馈源与接收机等6个子系统。其中馈源支撑系统由6个固定铁塔、6根钢索和馈源平台(舱体包括馈源舱、AB轴、Stewart平台)组成[2],可视为一个巨型柔性并联机构。钢索的一端固定于馈源舱体的铰接点上,另一端通过铁塔顶端的定滑轮与电机相连。天文观测时,6台电机协调改变6根钢索的长度,拖动馈源平台在反射面之上高约140 m、直径约200 m的球冠上运动。此时,钢索的跨度已经很大,它在空间的曲线形状不能简化为直线,而呈悬链线状[3]。

图1 FAST示意图
Fig.1 Illustration of the FAST
近代以来,随着悬索结构在桥梁、建筑等方面的应用,许多学者都在悬链线的解析法、有限元法分析中做过大量有益的尝试。由于悬链线的解析解为超越函数,在分析和计算时给人们带来不便,人们进而提出许多简化方法,其中尤以抛物线理论最为著名。抛物线是简单的二次函数,这大大简化了对悬索的分析和计算,在FAST模型实验中获得较好的应用[4]。
在FAST馈源支撑系统中,铰接点和高塔出索点相当于钢索的两个支点。在两个支点之间,钢索上仅受重力作用,没有其他载荷。由于人们主要关注钢索在两个支点处的受力情况,因此作者由悬链线解析解入手,从索力、索长表达式出发,提出赝曲线模型,对悬链线模型进行简化。
1 无荷悬索的悬链线
对于位于均匀重力场的悬索,做出如下假设[5]:(1)悬索只受拉力,不能受压或受弯;(2)忽略悬索的局部弯折;(3)悬索工作在弹性阶段。
对FAST系统,以一根钢索为分析对象,记钢索与馈源舱的铰接点为B,钢索与高塔定滑轮出索点为A。钢索除在A、B两支点受到支反力外,还要受自身重力作用,单位长度的钢索所受重力为q,其受力情况如图2。h和l分别为A、B两点之间的竖直和水平距离,σ为TB与水平面的夹角。
取钢索上的一段线元ds,如图3。
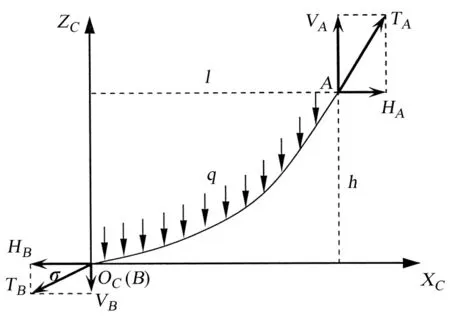
图2 钢索的受力分析

图3 钢索上的一段线元
由力平衡条件可得[6]:
(1)
整理可得:
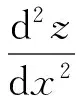
(2)
(2)式即为钢索的微分方程式。又有(ds)2=(dx)2+(dz)2,则(2)式可写为:
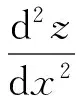
(3)
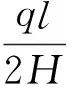
(4)
将边界条件
(5)
代入上式,可得:
(6)
(4)式、(6)式就是精确的悬链线表达式,该模型称为悬链线模型,它真实地反映了悬索的重力特性。悬链线表达式是一个超越函数,它将钢索的位形与钢索的索力联系起来,钢索的几何特征与它的受力特征密切相关。由(4)式、(6)式可得索长L:
(7)
整理得:

(8)
(8)式中的shλ/λ即反映了钢索由于垂度而产生的弯曲。
对A点列出力矩平衡方程,可得到VB。记:
则钢索的拉力为:
(9)
(10)
由(4)式、(6)式可以得到悬链线的垂度f表达式:
(11)
对(11)式求导,并令其等于0,可得取最大垂度点的横坐标:
(12)
将(4)式、(6)式中C2代入上式并整理可得:

(13)

2 悬链线的抛物线简化
由于(3)式的右侧实际上是无穷级数的形式,考虑到应用的便利性,人们往往将(2)式的右侧近似为一个常数,从而得到悬链线模型的简化模型——抛物线模型。对(2)式的右侧取不同的常数,便得到不同的近似模型。

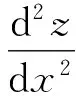
(14)
对(14)式两边积分,并应用边界条件(5),可得:
(15)
将λ=ql/2H代入(15)式,可得:

(16)
(13)式、(16)式就是仅受重力作用下钢索的抛物线形式的解析表达式,该模型称为抛物线模型。
对(16)式在A点求导数,可得到VB:
(17)
HB、VA、HA的表达式分别与(9)、(10)式对应项相同。比较(9)和(17)式可以看出,应用(15)式、(16)式所描述的抛物线表达式,部分地考虑了钢索自重的影响。
在XC轴中点处,即
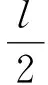
(18)
处抛物线函数取得垂度最大值:
(19)
将(19)式代入(15)式,可以得到用垂度最大值表示的抛物线表达式[4]:

(20)
根据(20)式并应用泰勒展开保留前两项,可得钢索的长度L:
(21)
3 悬链线的赝曲线简化
在悬链线模型中,索长和索力的表达式都是超越函数,有赖于对λ的求解结果。在λ较小的情形下考虑当

(22)
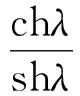
(23)
时,(8)式简化为:

(24)
(9)式中的VB简化为:

(25)
对比(9)、(17)和(25) 3式可见,赝曲线模型与抛物线模型一样,考虑了绳索自重的力矩作用,但没有考虑由于悬连线而导致的重心位置的改变。对比(8)式和(24)式,赝曲线模型实际上将悬链线模型中的sh2λ/λ2项忽略,钢索的长度计算退化为直线情形。因此称这种模型为赝曲线模型,如图4。
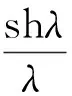

(26)
将(8)式代入(26)式,并应用泰勒展开只保留第1项整理得
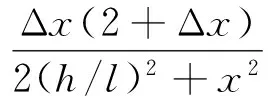

图4 赝曲线模型
Fig.4 Illustration of the Pseudo-Curve model
容易证明,当λ>0时,函数x=shλ/λ>1,则2(h/l)2+x2>1,因此
|σ1|<Δx(2+Δx)
若取Δx(2+Δx)<10%,则|σ1|必然小于10%。即当λ∈(0, 0.538)时,由于式的近似而引入到钢索长度的相对误差|σ1|一定小于10%。
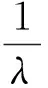

(27)
定义相对误差:



(28)
图5展示了不同k值情形下,σ2随λ的变化情况。表1为k取不同值时,满足|σ2|=10%的λ值,记为λC。

图5σ2随λ的变化情况
Fig.5 Relative errors at different values ofk
在应用中,人们往往难以获得比较精确的索力,因此可以适当增大σ2的允许上限,这时λ的上限值也会随着增加。一般地,当λ<0.538时,可以应用赝曲线模型估算索长,再利用解算出的VB来校验模型的准确性。
赝曲线模型没有给出钢索的解析表达式,而是关注于钢索的索长与B点的支反力。在巨型柔性连接的并联机构的建模中,因柔索悬链线方程带来非线性,且索长、索力等参数事先均未知。在一定条件下引入赝曲线模型后,将非线性方程组简化成线性方程组,保证解算精度的同时提高了解算效率。
表1k取不同值时的λC和σ1的最大值
Table1ValuesofλCandthemaximaofσ1atdifferentkvalues

kλCmax(σ1)/%1.000.4386.561.410.3905.171.730.3584.352.000.3343.772.240.3163.37
4 赝曲线模型与抛物线模型的关系
对比(13)和(18)式,抛物线表达式将钢索垂度的最大值取在了x0=l/2处。当λ满足(22)式时,(13)式蜕化为(18)式。若已知抛物线垂度最大值为f0和(5)式所示边界条件,则可得到(20)式所示抛物线表达式。这实际上是对双曲正弦函数shλ做泰勒展开,并只保留第1项的结果。
如果将抛物线的最大垂度取为(19)式,则可以由(20)式得到(15)式、(16)式。对比(17)式和(9)式,当λ满足(23)式时,(9)式蜕化为(17)式。
这说明抛物线模型中实际上暗含了(22)式所示条件,将这个条件应用于(8)式,即得出的赝曲线模型的结论(24)。如果抛物线模型中还满足(19)式,则该抛物线模型暗含了(23)式,将其应用于(9)式,即可得出赝曲线模型的结论(25)。
5 数值算例
以巨型柔性连接的并联单三角机构为例,其结构如图6。该机构的上平台为静平台,下平台为动平台。6台电机协调动作,牵引6根钢索改变长度,实现下平台的运动,并达到一定的位姿要求。建立如图6所示静坐标系C1[X-Y-Z]和动坐标系C2[XW-YW-ZW]。
当下平台处在静平衡状态时,6根钢索对下平台的驱动力F=[F1F2…F6]T与下平台载荷[GM(G)]T间的关系为[7]:

图6 巨型柔性连接的并联单三角机构
Fig.6 Illustration of a large 6-SPS
(29)

在方程(29)中,各已知参数和输入量见表2,需要求解未知参数F。要获得切线方向,就需要知道悬链线参数λi的信息,进而需要知道Hi。这样由于悬链线超越函数的引入,方程(29)的左边就成为一个关于F的非线性表达式,求解方程(29)便需要使用迭代法。为了避免使用迭代法,使用赝曲线模型代替悬链线模型,这样便可以获得简洁的索长和索力表达式,方程(29)作为线性方程组,求解相对简便。

表2 已知参数和输入量
表3展示了使用赝曲线模型和悬链线模型的求解结果。从表中悬链线模型得出的λ可以计算λchλ/shλ的均值为1.018,shλ/λ的均值为1.009,符合假设条件(22)、(23)。从表3可见,赝曲线模型得到的结果满足模型简化的要求。更为重要的是,由于引入赝曲线模型,解方程组(29)时只需解一次线性方程组,而无需使用迭代法求解多次线性方程组,从而大大节省解算时间,提高解算效率。

表3 悬链线模型与赝曲线模型的求解结果比较
6 结 论
(1)赝曲线模型主要关注钢索的长度和支点索力,当λ<0.538时,悬链线模型可以简化为赝曲线模型。在使用赝曲线模型计算完毕后,可以利用得到的λ考察是否满足(22)式、(23)式。
(2)抛物线模型可以推出赝曲线模型的结论(24)。如果将(2)式的ds/dx取为L/l,则这种抛物线模型可以得出赝曲线模型的结论(25)。
(3)由于赝曲线模型给出了钢索长度和支点索力较为简洁的表达式,因此在巨型柔性并联机构等方面在保证求解精度的同时,可以较好地提高求解效率。
[1] Nan Rendong. Five hundred meter aperture spherical radio telescope (FAST) [J]. Science in China: Series G Physics, Mechanics & Astronomy, 2006, 49(2): 129-148.
[2] 朱文白. FAST望远镜天文规划和馈源支撑的相关研究[D]. 北京: 中国科学院国家天文台, 2006: 16-18, 70-75.
[3] Li Hui, Nan Rendong, Kaercher H, et al. Working space analysis and optimization of the main positioning system of FAST cabin suspension[C]// Proceedings of SPIE. Astronomical instrumentation, Ground-based and airborne telescopes II. Bellingham: SPIE-International Society for Optical Engine, 2008: 70120T-1-70120T-11.
[4] 姚蕊, 唐晓强, 李铁民, 等. 大型射电望远镜馈源定位3T索牵引并联机构分析与设计[J]. 机械工程学报, 2007, 43(11): 105-109.
Yao Rui, Tang Xiaoqiang, Li Tiemin, et al. Analysis and design of 3T cable-driven parallel manipulator for the feedback’s orientation of the large radio etsescope[J]. Chinese Journal of Mechanical Engineering, 2007, 43(11): 105-109.
[5] 沈锐利. 悬索桥主缆系统设计及架设计算方法研究[J]. 土木工程学报, 1996, 29(2): 3-9.
Shen Ruili. Calculation methods for design and erection of cable curve of suspension bridge[J]. China Civil Engineering Journal, 1996, 29(2): 3-9.
[6] 杜敬利, 段宝岩, 仇原鹰, 等. 舱索系统的非线性静力学分析与索长解算[J]. 机械科学与技术, 2006, 25(8): 946-948.
Du Jingli, Duan Baoyan, Qiu Yuanying, et al. Nonlinear static analysis and cable-length solution of a cabin-cable system[J]. Mechanical Science and Technology, 2006, 25(8): 946-948.
[7] 仇原鹰, 段宝岩, 盛英, 等. Stewart平台的运动奇异性与力奇异性研究[J]. 西安电子科技大学学报, 2001, 28(2): 202-206.
Qiu Yuanying, Duan Baoyan, Sheng Ying, et al. Research on the kinematic singularity and the force singularity of the Stewart platform[J]. Journal of Xidian University, 2001, 28(2): 202-206.
