GPS信号延时相乘捕获算法的检测率仿真*

范江涛，马冠一

(1. 中国科学院国家天文台，北京 100012；2. 中国科学院研究生院，北京 100049)

信号捕获是全球定位系统接收机工作的首要环节[1-2]。随着全球定位系统的广泛应用，全球定位系统信号捕获性能的改善和特殊环境下全球定位系统信号捕获的研究成为重要的研究课题。相应地，信号的快速捕获，检测率的提高，抗干扰特性，高动态、弱信号、多径环境下信号的捕获成为研究的热点[3]。传统的全球定位系统信号捕获过程中存在着多普勒频偏的影响，多普勒频偏主要来源于全球定位系统卫星与接收机相对运动引起的多普勒效应和接收机晶振的频偏[4]。全球定位系统信号捕获需要同时对多普勒频偏和初始码相位进行搜索，这个搜索过程为二维搜索，搜索次数决定了捕获时间。如果频偏大，搜索次数会显著增加，从而增加捕获时间。如果多普勒频偏估算不准确，还会导致传统捕获算法的检测率下降。而且多普勒频偏的搜索间隔会限制捕获中积分时间的长度，不利于信噪比的提高[4-7]。

延时相乘捕获算法，也称为差分捕获算法，它利用延时相乘操作，可以消除信号中频偏的影响[8-10]，能解决上述传统捕获算法中频偏引起的问题。该算法分别对信号的初始码相位和频偏做一维搜索，搜索次数少，捕获时间短；而且可以进行长时间积分，提高信噪比，特别适用于受频偏影响大的高动态信号环境[11]。另一方面，该算法中的延时相乘操作会增加噪声量，降低信噪比和检测率，恶化捕获性能[3-4]。为此文[10]提出了把多个延时相乘结果结合起来提高信噪比的算法，从而改善了捕获性能。

为了从根本上保证延时相乘捕获算法的性能，本文针对该算法的噪声特性和检测率进行仿真分析，并提出了提高检测率的方法。本文第1节介绍延时相乘捕获算法的原理和数学模型，并给出一个捕获实例。第2节基于蒙特卡罗方法对延时相乘算法中得到的积分结果及其噪声分布进行仿真分析。第3节仿真计算了延时相乘捕获算法的检测率，通过检测率随虚检率的变化关系说明检测性能。提出并仿真说明减小噪声带宽和延长积分时间可以改善检测性能。第4节给出全文的结论。

1 延时相乘捕获算法的原理

延时相乘捕获算法通过一个延时相乘运算消除信号中的频率项，算法的原理框图如图1。信号经过延时相乘后，与接收机本地产生的延时相乘扩频码信号做相干积分，本地扩频码信号做的延时相乘操作与对信号做的延时相乘操作相同。用积分结果作检测值来判断信号是否存在，并根据最大检测值的位置获取初始码相位信息。

图中S(t)为接收机接收的全球定位系统信号，n(t)为接收的噪声信号。S(t)的数学模型为：

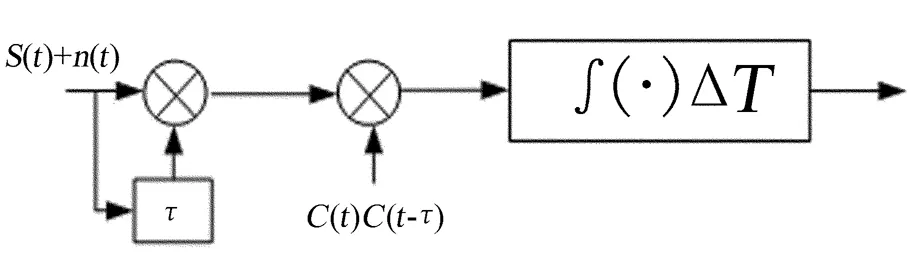
图1 延时相乘捕获算法的原理框图

Fig.1 Block diagram of the Delay-and-Multiply method

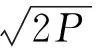
(1)

式中，P为信号功率；D(t)为数据调制信息；C(t)为扩频码信息；fIF为信号的中频频率；fD为多普勒频偏；φ0为初始载波相位。假设噪声n(t)为高斯白噪声。

如果延时相乘的时延为τ，则噪声和信号延时相乘后的结果可表示为：

[S(t)+n(t)][S(t-τ)+n(t-τ)]=S(t)S(t-τ)+S(t-τ)n(t)+S(t)n(t-τ)+n(t)n(t-τ)

(2)

其中第1项为信号与信号做延时相乘的结果，利用(1)式可知：

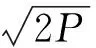
由于τ≪1 ms，因此D(t)D(t-τ)≈1。又由于积分过程相当于一个低通滤波，可以略去信号相乘后的高频项，因此式子可以简化为：

S(t)S(t-τ)≈P[C(t)C(t-τ)]cos[2π(fIF+fD)τ]

(3)

由于τ为固定值，且fD≪fIF，选取合适的τ值，使2πfIFτ=2kπ，则式中的cos(2π(fIF+fD)τ)≈1，则(3)式进一步简化为：

S(t)S(t-τ)≈P[C(t)C(t-τ)]

(4)

因此只要选取合适的τ值对信号做延时相乘，可以消除信号中频偏的影响。式中C(t)C(t-τ)为一个新的扩频码序列，通过在本地产生一个相同的C(t)C(t-τ)扩频码序列搜索码的初始相位，所得到的初始码相位与延时相乘之前信号的初始相位相同。其中要求τ大于1个码片时间，且为码片间隔的整数倍，以保证C(t)C(t-τ)仍为Gold码序列。

由于消除了频偏的影响，只需要对信号的初始码相位进行一维搜索，即可以得到初始码相位并判断信号是否存在。在频偏大和频偏有变化率的情况下，信噪比也不会降低。而且D(t)D(t-τ)≈1，即没有数据调制项的影响，可以进行长时间积分提高信噪比。在判断信号存在后，可以对信号解扩，然后再对信号频率进行一维搜索，得到频偏信息[3-4]。

从(2)式可以看出，噪声项变为3项，S(t-τ)n(t)、S(t)n(t-τ)、n(t)n(t-τ)，噪声量相比n(t)增加了。噪声量的增加导致信噪比降低，检测率下降。在正常的载噪比条件下，即载噪比为40～45 dB-Hz时，采用1 ms的积分时间无法检测到信号，需要5 ms以上的积分时间，才能检测到信号[9]。对采集的全球定位系统信号在软件接收机中使用延时相乘捕获算法捕获信号，使用的全球定位系统信号数据文件来自文[12]，信号的采样率为16.367 6 MHz，中频为4.130 4 MHz，对PRN22码信号进行了捕获。捕获结果如图2。

图中横坐标为采样点数，从图2(a)和图2(b)可以看出，受噪声大的影响，使用1 ms积分做捕获时，无法判断信号是否存在，使用5 ms积分，可以捕获到明显的信号相关峰，判断信号存在，并得到初始码相位信息。从捕获结果中得到的初始码相位信息与传统捕获算法得到的初始码相位信息一致。从这个捕获实例可以看出延时相乘捕获算法受噪声量增加影响，1 ms积分时间无法捕获信号，检测性能不佳，但是通过延长积分时间可以提高检测性能。

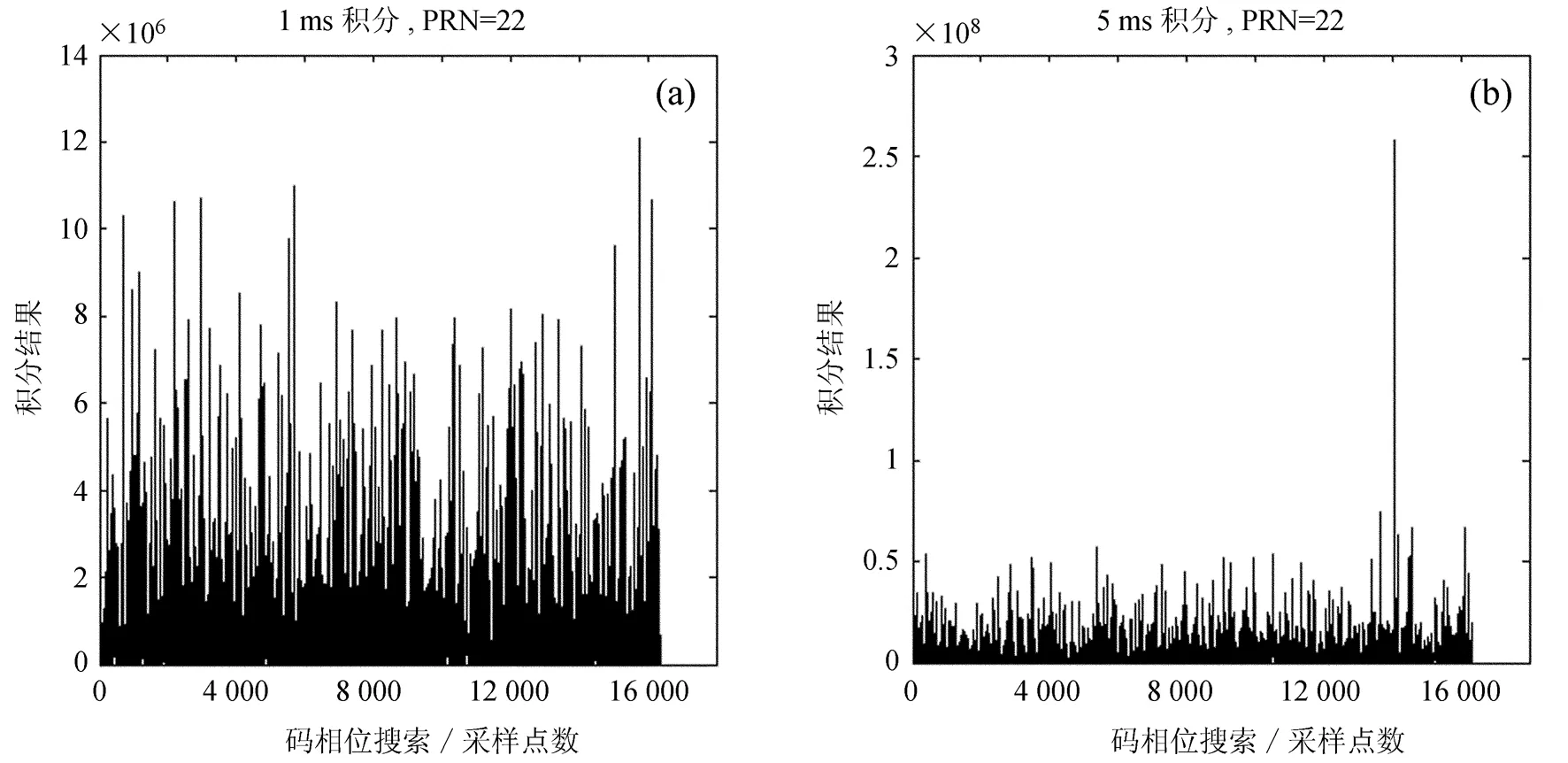
图2 (a) 延时相乘捕获算法1 ms积分捕获结果; (b) 延时相乘捕获算法5 ms积分捕获结果

Fig.2 (a) Acquisition results of the Delay-and-Multiply method with 1ms integration time; (b) Acquisition results of the Delay-and-Multiply method with 5ms integration time

2 对噪声的仿真分析

针对延时相乘捕获算法中噪声显著增加的特点，在分析算法的检测率之前，需要分析算法中的检测变量即输出的积分结果的噪声分布。

从理论上分析，根据中心极限定理，延时相乘算法最后积分结果的噪声分布近似为高斯分布。这是因为积分结果是每个采样点的噪声值通过算法运算后的结果相加，每个采样点的噪声值相互独立，当积分点数很多时，大量相互独立的分布相加的结果趋于高斯分布。

由于延时相乘运算为非线性计算，从理论上计算不易得到积分结果的噪声分布的准确数学表达式。但是只要能够用数值算法定义或近似模拟的模型，都可以用蒙特卡罗方法仿真计算，不需要做解析分析[13]。因此本文采用蒙特卡罗方法分析算法中噪声的分布。

根据图1延时相乘捕获算法的原理，在输入端输入高斯白噪声，对输出的积分结果基于10 000次计算做统计，得到的积分结果的噪声和噪声分布如图3。

图3中上图为每次蒙特卡罗计算的结果，下图为对仿真结果的噪声分布统计，图中的曲线为一条高斯分布概率密度函数曲线，可以看出积分结果的噪声分布与高斯分布近似。因此可以用高斯分布近似表示延时相乘算法中积分结果的噪声分布。

3 对检测率的仿真分析

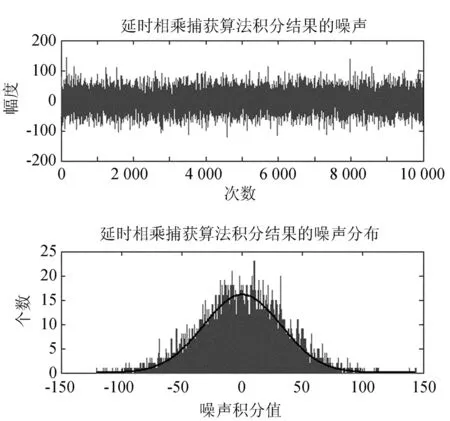
图3 延时相乘捕获算法噪声积分结果及其分布

Fig.3 The distribution of noise of the integration result of the Delay-and-Multiply method

用检测率可以衡量捕获算法的性能。在相同信号载噪比和虚检率条件下，检测率越高，说明捕获算法性能越好。检测率(Pd)为在信号存在时，检测结果即算法中的积分结果超过检测门限的概率。虚检率(Pf)为信号不存在时，噪声的检测结果高于门限的概率[1]。在单次恒虚检试验中，检测门限通过预先设置某一虚检率确定。通常通过检测率与虚检率的关系说明捕获算法的检测率特性[14]。

按照算法的原理，采用蒙特卡罗方法，选取如下仿真条件：C/N0为45 dB-Hz，信号功率归一化为1，采样率为20 MHz，信号中频为5 MHz，信号为全球定位系统的C/A码信号。基于10 000次计算结果的统计，得到的延时相乘捕获算法中信号存在和不存在时积分结果的分布如图4，以及基于图4的结果得到的检测率随虚检率的变化关系，如图5。

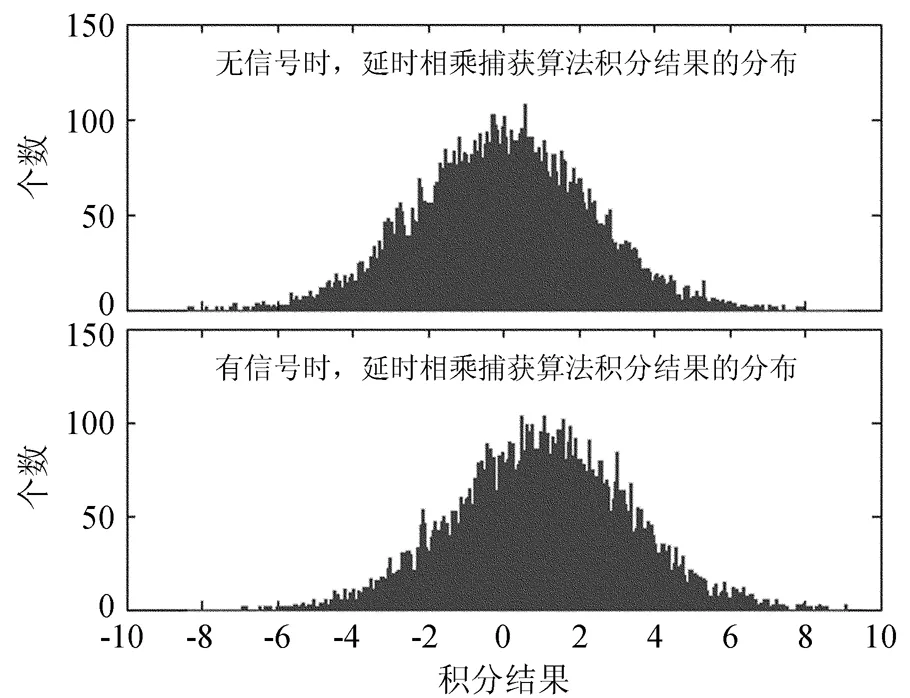
图4 延时相乘捕获算法积分结果的分布

Fig.4 The distribution of integration result of the Delay-and-Multiply method

图5 延时相乘捕获算法检测率与虚检率关系

Fig.5 The relation between Pd and Pf in the Delay-and-Multiply method

从图4可以看出，积分结果分布的方差比较大，信号存在时只改变了积分结果的均值，对积分结果的方差没有明显的影响。积分结果的方差大是由于算法中噪声量增加导致的。从图5的结果可以看出检测率随虚检率的增大上升缓慢，在某一固定虚检率下，检测率相对于虚检率不高。

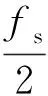
可以看出，同样是采用1 ms积分，相比图5，4 MHz采样时检测率有所提高。在虚检率为0.1时，20 MHz采样时的检测率为0.2；4 MHz采样时的检测率为0.4。从图6中各积分时间的检测率结果还可以看出，延长积分时间，检测率明显提高。在虚检率为0.1时，1 ms积分时的检测率为0.4，5 ms积分的检测率为0.8，10 ms积分的检测率为0.97。这说明通过减小噪声带宽和延长积分时间可以提高延时相乘捕获算法的检测率。

为了反映算法检测率随C/N0的变化，在4 MHz采样率，5 ms积分条件下，通过蒙特卡罗方法计算了在C/N0分别为35、40、45 dB-Hz时的检测率随虚检率的变化，如图7。

从图7可以看出，在虚检率为0.1时，载噪比为35 dB-Hz、40 dB-Hz、45 dB-Hz的检测率分别为0.15、0.3、0.83，算法的检测特性随C/N0上升而改善。这说明高载噪比条件有利于使用延时相乘捕获算法。

4 结 论

本文介绍了延时相乘捕获算法的原理，分析了该算法可以消除频偏影响的特点和噪声量增加的问题。由于不受频偏影响，延时相乘捕获算法搜索次数少，可以进行长时间积分提高检测率，适用于频偏大和频偏变化率大的信号环境。但是噪声量大的缺点需要加以改善。

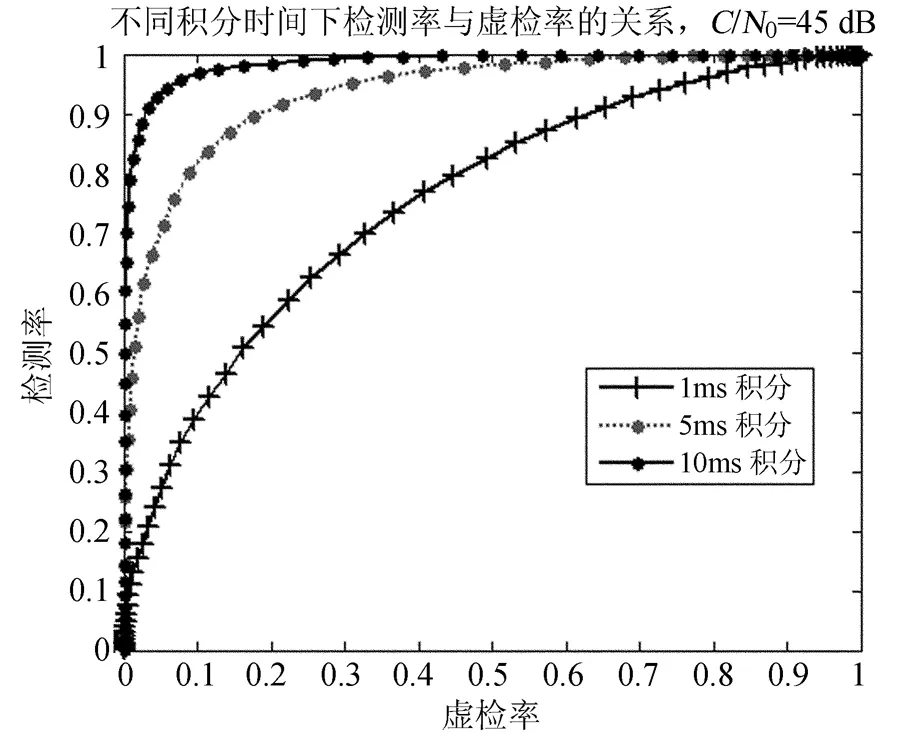
图6 延时相乘捕获算法，采样率降为4 MHz的检测率

Fig.6 The relation between Pd and Pf in the Delay-and-Multiply method forfs=4MHz

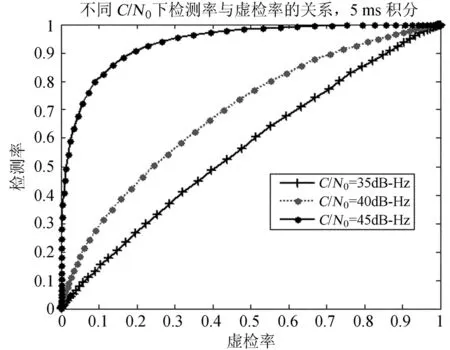
图7 不同C/N0条件下延时相乘捕获算法检测率

Fig.7 The relations between Pd and Pf for different values ofC/N0of the Delay-and-Multiply method

通过蒙特卡罗方法仿真计算了延时相乘捕获算法的噪声分布和检测率与虚检率的关系。对噪声做延时相乘后的积分结果符合高斯分布。在正常信号条件下，延时相乘捕获算法的检测率不高。为此采用了通过减小噪声带宽和延长积分时间提高检测率的方法。减小噪声带宽可以采用降低采样率和中频频率来实现。仿真表明，在虚检率为0.1时，20 MHz采样时的检测率为0.2，4 MHz采样时检测率为0.4；在采样率为4 MHz，载噪比为45 dB-Hz，虚检率为0.1时，1 ms、5 ms、10 ms积分的检测率分别为0.4、0.8、0.97。最后仿真计算了检测率与虚检率的关系随载噪比的变化，结果表明高载噪比条件有利于使用延时相乘捕获算法。

[1] Elliott Kaplan, Christopher J Hegarty. Understanding GPS, principles and applications[M]. Boston: Artech House, 2006.

[2] Misra P, Enge P. Global positioning system: signals, measurements and performance[M]. Lincoln, MA: Ganga-Jamuna Press, Dec, 2001.

[3] 谢钢. GPS原理与接收机设计[M]. 北京: 电子工业出版社, 2009.

Gang Xie. Principles of GPS and receiver design[M]. Beijing: Publishing House of Electronics Industry, 2009.

[4] James B Y Tsui. Fundamental of global positioning system receivers, a software approach[M]. Wiley-Interscience, 2005.

[5] Borio D, C O'Driscoll, G Lachapelle. Coherent, non-coherent and differentially coherent combining techniques for the acquisition of new composite GNSS signals[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(3): 1227-1240.

[6] Borio D. GNSS acquisition in the presence of continuous wave interference[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 46(1): 47-60.

[7] Borio D, Sokolova N, Lachapelle G. Doppler measurement accuracy in standard and high-sensitivity GNSS receivers[J]. IEEE IET Radar, Sonar & Navigation, 2011, 5(6): 657-665.

[8] David M Lin, James B Y Tsui. Comparison of Acquisition Methods for Software GPS Receiver[C]// ION GPS 2000, Salt Lake City, UT.

[9] David M Lin, James B Y Tsui. Acquisition schemes for software GPS receiver[EB/OL]. [2012-02-21]. http://gps-ttff.tripod.com/Schemes.pdf.

[10]Surendran K Shanmugam. Narrowband interference suppression performance of multi-correlation differential detection[C]// Proceeding of ENC-GNSS. Geneva, 2007.

[11]Wang Shicheng, Yang Dongfang, Liu Zhiguo, et al. Simulation study on a novel high-dynamic GPS software receiver[J]. The International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 2009, 28(6): 1386-1401.

[12]Kai Borre, Dennis M Akos, Nicolaj Bertelsen, et al. A software-defined GPS and galileo receiver, a single-frequency approach[M]. Birkhauser Boston, 2007.

[13]William H Tranter, K Sam Shanmugan, Theodore S Rappaport, et al. Principles of communication systems simulation with wireless application[M]. Pearson Education, 2004.

[14]Daniele Borio, Cyrille Gernot, Florence Macchi, et al. The output SNR and its role in quantifying GNSS signal acquisition performance[C]// Proceeding of ENC-GNSS. Toulouse, 2008: 22-25.