地平式望远镜AGU标校模型与仿真试验*

2013-12-16卢晓猛王建峰王汇娟米琳莹

天文研究与技术 2013年2期

卢晓猛，王建峰，王汇娟，米琳莹

(中国科学院国家天文台，北京 100012)

在建的2.5 m望远镜计划安装在俄罗斯的Kislovodsk太阳观测站。该望远镜为地平式结构，有一个卡焦焦点和两个耐氏焦点，其中卡焦和耐焦N1配置有机械消转器和自动导星单元(Automatic Guiding Unit, AGU)，自动导星单元本体安装在像场的消旋机构上。当像场消旋机构旋转时，自动导星单元本体会随之同步旋转。

在天文研究中为了观测暗弱恒星，不改变望远镜主镜口径和光学效率的前提下延长CCD曝光时间是必然的手段。而延长曝光时间需要望远镜控制系统具备比较高的指向与跟踪精度，能够实现对恒星的凝视观测。2.5 m望远镜将使用Tpoint建立方位轴、俯仰轴和机械消转轴的周期性误差修正模型，基于偏置导星方法使用自动导星单元消除望远镜的瞬时性跟踪误差。

2.5 m望远镜口径为2.5 m，系统焦比F/8，自动导星单元使用的CCD相机像元尺寸为9.9 μm×9.9 μm，靶面分辨率为659×493，其视场约为67.3″×50.3″。如果使用V星等亮于11.5等、完备度90%的第谷2作为导星星表，则平均每个视场内约有0.016颗恒星。按照设计，2.5 m望远镜使用亮于15等作为导星星表，由USNO A2.0提取统计，平均每个视场内约有0.093颗恒星。因此必须控制自动导星单元定位将参考星引入视场，同时必须消除自动导星单元旋转带来的像场旋转，才能精确地计算导星偏差，从而实现主视场对观测恒星的高精度跟踪。

如图1，自动导星单元可以在两维运动。一维是平移机构沿着丝杆滑动；另一维是丝杆中心绕轴在本体基平面上旋转，构成图2的等效运动，实现对光学视场内参考星的定位。这种运动控制方式与云南天文台1 m望远镜的偏置导星单元工作原理有所不同[1]。

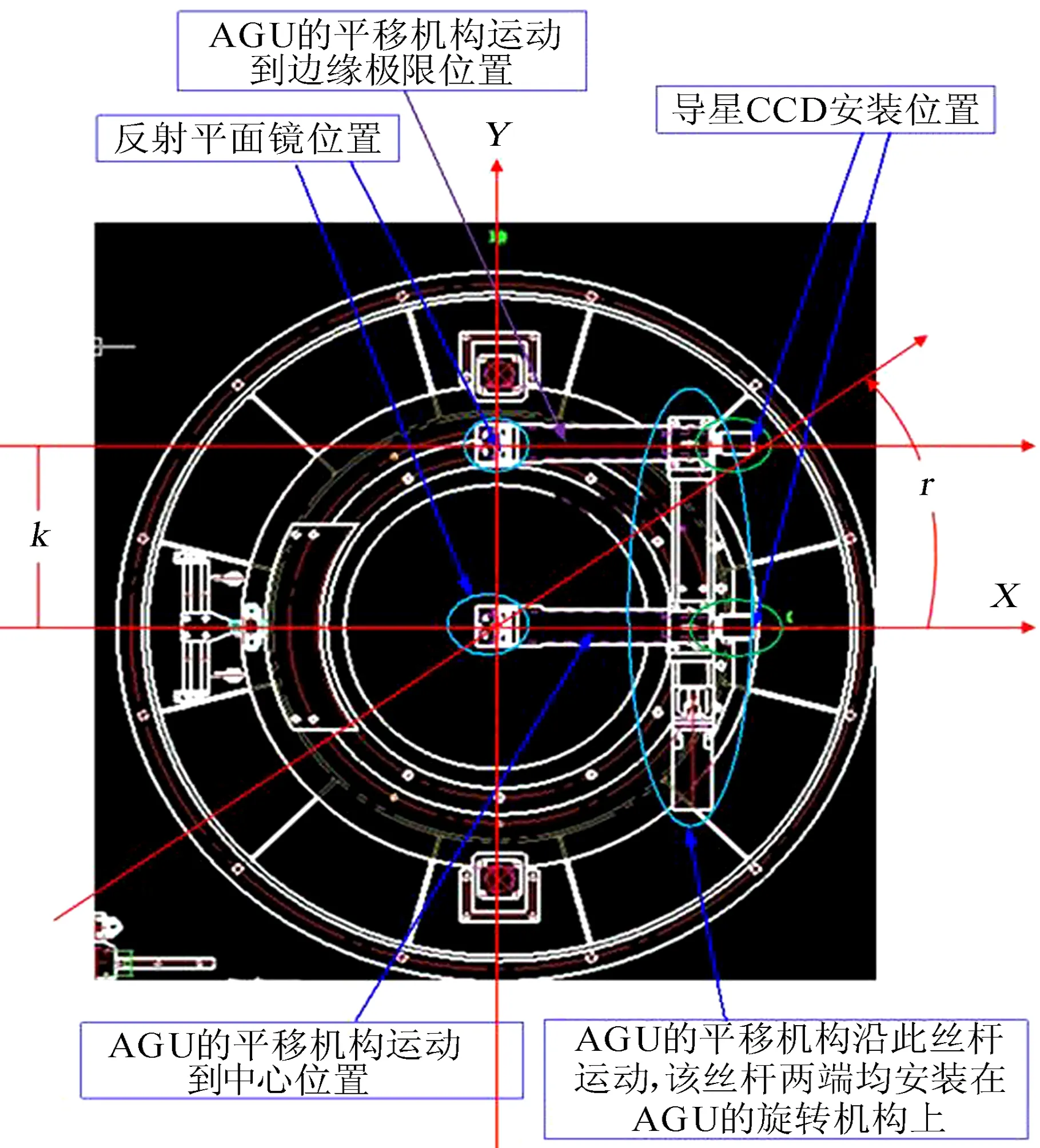
图1 自动导星单元运动方式

Fig.1 The motion modes of the AGU

将自动导星单元的平移运动定义为k模式，将旋转运动定义为r模式，将CCD的X轴与赤道α轴夹角定义为θ。借助恒星赤道坐标的理想平面投影，建立k-r坐标系与赤道α-δ坐标系的齐次修正方程，实现自动导星单元对参考星的定位功能。使用恒星拖尾法建立r角与θ角的齐次修正方程，拟合CCD图像(Δx, Δy)与赤道坐标系位置偏差(Δα, Δδ)的关系，消除像场旋转带来的位置计算误差。

1 中心指向修正模型

图2 自动导星单元等效运动

Fig.2 Apparent motion of the AGU

中心指向修正模型是为了建立赤道系(α,δ)→轴系(k,r)的映射关系，根据赤道坐标定位自动导星单元，解决参考星进入视场问题。

借助赤道系(α,δ)的理想平面投影(X,Y)，以及(k,r)对应的直角坐标(x,y)，通过建立线性修正方程简化模型拟合复杂度。即建立：

(α,δ)⟹(X,Y)⟹(x,y)⟹(k,r)

(1)

实现(α,δ)→(k,r)的数学转换[2]。

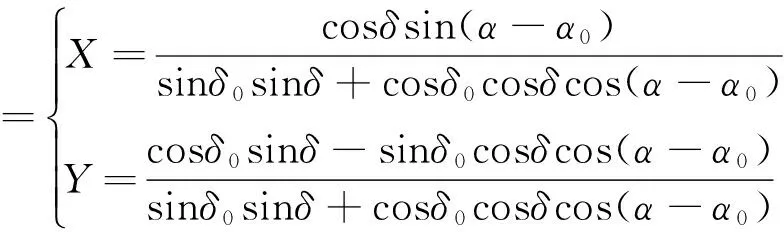
(2)

式中，(α0,δ0)是望远镜指向位置；(α,δ)是参考星位置；(X,Y)是参考星在理想平面的投影坐标。

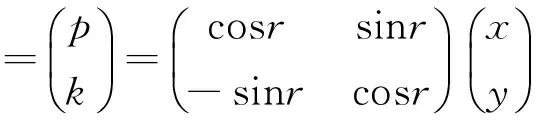
(3)

式中，(k,r)是自动导星单元轴系位置；(x,y)是对应的直角系位置。

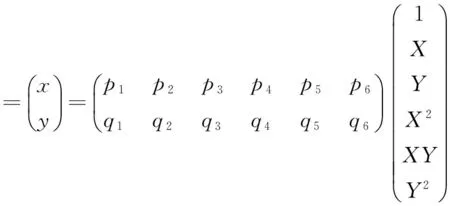
(4)

(5)

使用最小二乘法建立F与(p1,p2,p3,p4,p5,p6)，G与(q1,q2,q3,q4,q5,q6)的齐次方程求解矩阵[3]：

和

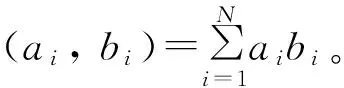
表1 中心指向修正模型对应的数据结构

2 像场旋转修正模型

像场旋转修正模型是为了建立CCD靶面坐标系(Δx, Δy)→赤道系(Δα, Δδ)的映射关系，根据星像像素偏差计算望远镜轴系偏差，消除由于r模式运动带来的像场旋转造成的位置计算误差。

对于本系统中自动导星单元导星CCD视场约1′来说，可以忽略视场形变。因此，假设(Δx, Δy)与(Δα, Δδ)平面投影夹角为θ，则有如下公式：

(6)

为了简化数学模型，规避极坐标系的圆周期，将θ与r转换到直角坐标系建立如下修正模型：

(7)

由此，可以如公式(5)一样，使用最小二乘法建立求解方程，并建立像场旋转修正模型。像场旋转修正模型对应的数据结构见表2。

表2 像场旋转修正模型对应的数据结构

3 仿真试验

2.5 m望远镜系统中控制自动导星单元实现对参考星的定位，以及根据参考星位置偏差量计算望远镜轴系误差，其精度由方位轴、俯仰轴、机械消转轴和自动导星单元本身的定位精度决定。方位轴、俯仰轴和机械消转轴使用Tpoint拟合其周期性误差，一般可以达到优于10″的定位精度。自动导星单元定位精度由测角精度、机械重复精度、控制精度和模型精度决定，需要确认使用本文论述的拟合方法不会为自动导星单元定位精度带来额外误差。

在仿真试验中，为k模式运动添加1‰的随机误差，r模式运动添加10′的随机误差，评估模型修正后在k-r坐标系和X-Y坐标系的残差。在赤经0°、赤纬40°位置使用9点拟合残差见表3。

表3中x残差和y残差由公式(3)微分计算传递误差：

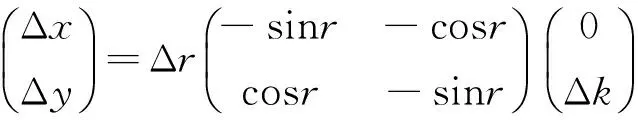
(8)

由仿真结果可以确定：当k模式运动中存在1‰的随机误差，r模式运动中存在10′的随机误差时，自动导星单元中心指向修正模型在XY坐标系中有约0.05测角计数误差。一般来讲，现代光栅尺、圆光栅等测量设备的精度都在角秒量级，0.05测角计数可以说明修正模型能够比较好地修正自动导星单元中心指向误差，不会为系统带来额外误差。

4 总结

本文给出两个数学修正模型，解决2.5 m望远镜自动导星单元系统工作中的两个问题：(1)由参考星的赤道坐标计算其控制位置，实现将参考星引入自动导星单元视场；(2)建立CCD靶面坐标系与赤道坐标系夹角随自动导星单元旋转角度的变化关系，可以由星像偏差量实时计算望远镜轴系偏差量，保证控制系统完成自动导星流程。

在数学模型建立过程中，借助球面坐标到理想投影平面坐标的映射关系，以及极坐标到直角坐标的映射关系，将非线性的矩阵求解方程转换为线性，在不损失拟合精度的同时简化了数学表达关系。