伽玛射线暴内光度和峰值能量关系的再研究*

尹 跃，柏 杨，张太荣，李明军

(六盘水师范学院物理与电子科学系，贵州 六盘水 553004)

伽玛射线暴(简称伽玛暴)是来自宇宙空间的一种短时标高能伽玛射线爆发现象，具有极高能、强爆发和瞬时性等特征，是自宇宙大爆炸以来人们所能观测到的宇宙中的最强烈的恒星级爆发现象。持续时间约为0.1～1 000 s，能段主要集中在10 KeV～1 MeV，典型光子流量为0.01～100 cm-2s-1[1]；由观测到的伽玛暴统计知道伽玛暴的空间角分布呈高度的各向同性, 其径向分布却不均匀,越远伽玛暴越多。伽玛暴的光变曲线非常复杂，不同的暴具有不同的时间结构，其光变曲线是由许多单脉冲组成的；尽管不同的伽玛暴具有不同的光变曲线，但是其能谱却非常相似，伽玛暴的能谱大部分都是非热连续谱，部分暴有一个很长的高能尾巴，有的甚至延伸到千兆电子伏(GeV)。

自从伽玛暴被发现以来，由于其高能量、强爆发、瞬时性等特征，人们对其神秘性一直具有浓厚的兴趣，现在对伽玛暴的研究已成为天体物理中的一个热点。伽玛暴的起源和本质是现代天体物理的一个难解之谜。要解开这个谜团，一般来说，可从下面4个方面着手：(1)研究暴的空间分布；(2)搜索暴的对应体；(3)研究暴的时间结构；(4)研究伽玛暴的能谱。伽玛暴的能谱在一次爆发中是随时间而变化的。其能谱反映了能量的大小和爆发源区域的粒子分布，能谱的变化能反映辐射区域的一些基本物理信息。只有当人们完全了解伽玛暴的起源，才能完全理解辐射区域的物理机制，也就能完全解释这些爆发现象。当前的理论几乎没有提供对这些暴数据的指引，但是暴的时间和谱的特性为这些爆发事件的起源提供线索并能对物理模型提供限制。因此研究伽玛暴的能谱对理解伽玛暴的物理本质非常重要。1993年，文[2]作者给出了一个能对伽玛暴能谱进行拟合的经验公式；之后文[3]作者指出同步辐射很可能是伽玛暴的辐射机制，文[4]作者则用幂律分布的相对论电子的同步辐射对一些伽玛暴能谱进行了拟合。

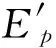
在本文的计算中采用H0=71 km s-1Mpc-1、ΩM=0.27、ΩA=0.73、H0为哈勃常数、ΩM为宇宙的平均物质密度、ΩA为宇宙的真空能密度。

1 样本的选择

选择文[13]2006年分析的BATSE能谱样本作为分析样本，文[13]作者在2006年对BATSE观测到的350个亮暴进行了系统全面的能谱分析，这些暴的时间分辨率和能谱分辨率都很高。他们根据伽玛暴的能流或者峰值光子流量从BATSE观测的2 704个暴中挑选出350个亮暴作为研究样本，其中短暴17个，长暴333个，他们利用五种不同的光子模型对350个伽玛暴能谱的时间积分谱和8 459个时间分辨谱进行分析得出不同的谱参数，并且比较了不同的光子模型，这是目前为止最新最全面而且数量最大的伽玛暴能谱分析样本。本文选择最广泛使用的Band光子模型拟合的能谱样本。

Band光子模型的经验公式是：

(1)

式中，Ec为拐折能量，其表达式为：

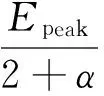
(2)

在(1)式中有4个参数：即振幅A、低能谱指数α、高能谱指数β以及vFv谱的峰值能量Epeak。在由Band光子模型拟合得到的结果中，为了得到更合理的统计样本，除掉了卡方值为-1的拟合参数，限制了高能谱指数，即取高能谱指数β<-2，除掉了Epeak值的误差大于Epeak值的90%的拟合参数，最后对每个暴的时间分辨谱的个数也进行了限制，只取能谱个数大于等于5的伽玛暴样本，由此选取了用Band光子模型拟合的185个伽玛暴能谱的时间积分谱和5 218个时间分辨谱作为研究样本。

2 分析结果

2.1 伽玛暴内光度和峰值能量的关系

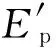
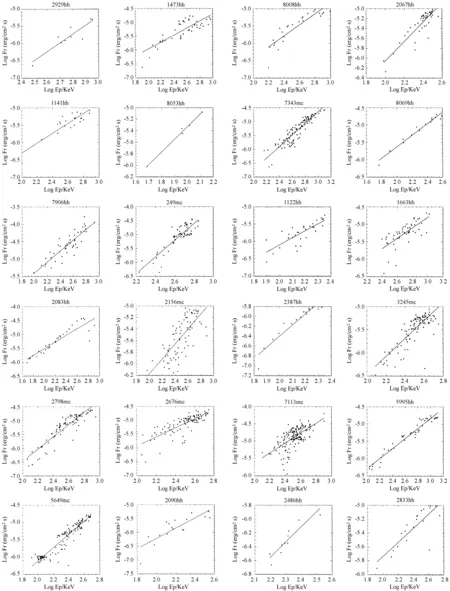
图1 24个GRB的观测流量与峰值能量的关系图

Fig.1 Observed fluxes as functions ofEpfor 24 GRBs

2.2 伽玛暴间光度和峰值能量的关系

Liso=4πdl2F

(3)

计算出185个GRB能谱的5 218个时间分辨谱的光度，这里F为观测流量；dl为光度距离。光度距离dl的计算公式为：

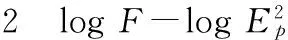
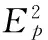
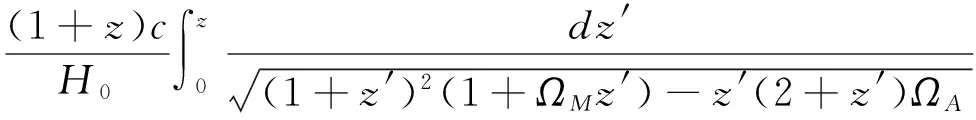
(4)

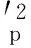
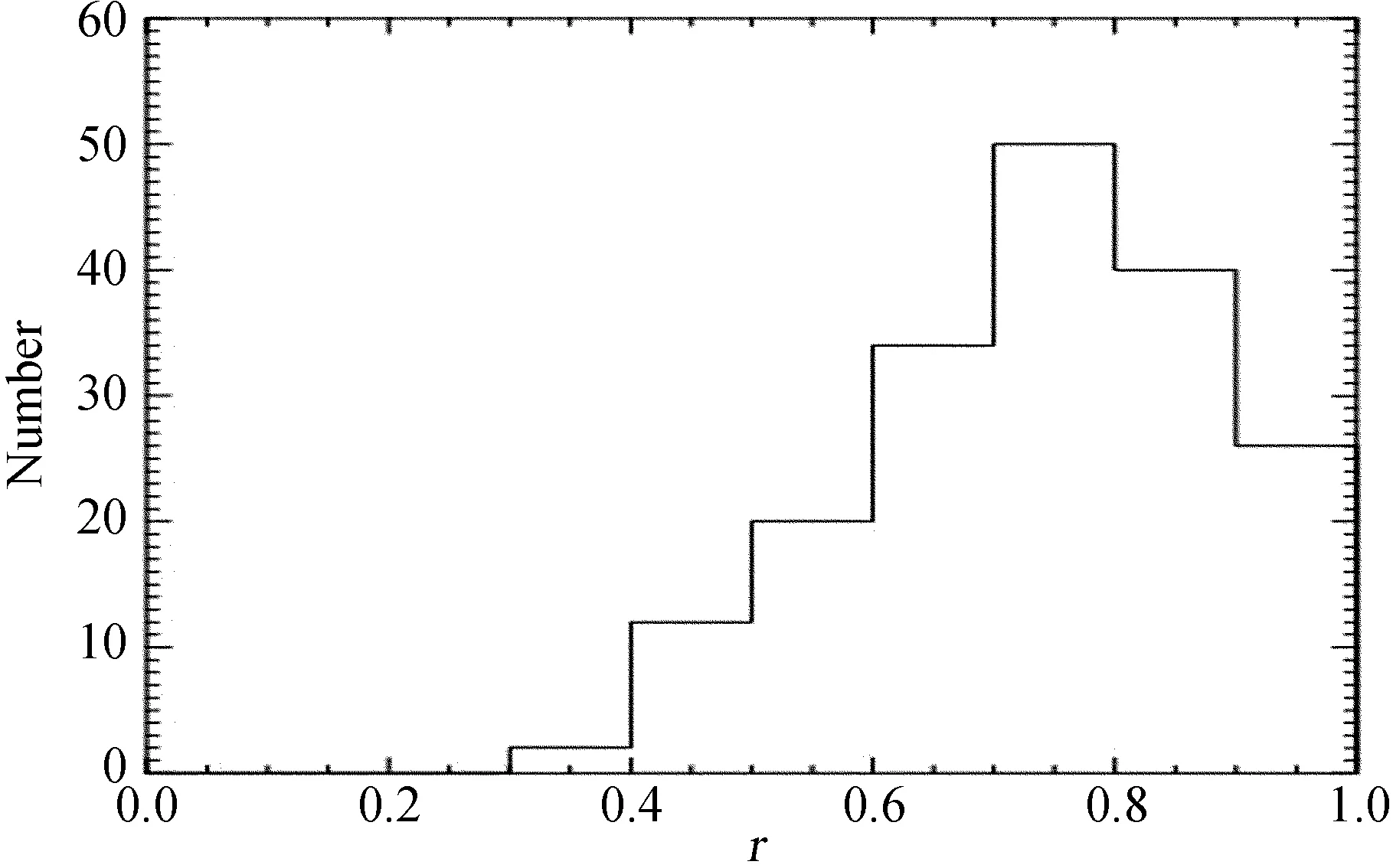
图3 收集到的174个GRB观测红移的累积概率分布图

Fig.3 Cumulative probability distribution of the observed redshifts of the collected 174 GRBS

图4 5 218个GRB时间积分谱的光度Liso,52与Ep(1+Z)的函数图形

Fig.4Liso,52as a function ofEp(1+Z) according to 5218 GRB spectra

3 对火球模型的限制

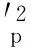
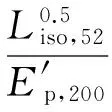
(5)

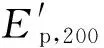
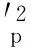
ω≈ζiR13

(6)

式中，ζi是综合内激波参数；R13是单位为1013cm的火球模型的半径。由Zhang和Meszaros文献中的式(23)可以得到在外激波模型中：

(7)

式中，ζe是综合外激波参数；σ1=σ/10σ是冷热光度部分的比值；Γ2.5=Γ/102.5Γ是火球的体洛伦兹因子；E53是以1053ergs为单位的总能量；n1是以10 cm-3为单位的媒介密度。

由式(6)可以看出，对内激波模型来说ω的值由伽玛射线发射区域的半径和ζi共同决定，ζi与激波参数有关，例如电子的分布量、电子均分因子、磁均分因子、电子螺距角和壳层之间的相对洛伦兹因子等，这些参数只与碰撞壳层的物理性质有关。然而，对于外激波模型，情形就变得更加复杂。从式(7)可以看出ω是由激波和环境参数共同决定的。

在伽玛暴内计算了每一个时间分辨谱所对应的ω值，并用线性模型ω∝kt研究了ω的变化，k值能很好地判断ω值的变化趋势，当k值的绝对值越大时ω值的变化越显著。分别做出了ω和k值的分布图(如图5～6)，从图可以看出ω和k值的主要分布范围分别是0.1～1和-0.03～0.03。这些结果表明对不同的伽玛暴以及在同一个伽玛暴内部的不同时间段的ω的值是不随时间变化的。

图5 5 218个能谱的ω分布图

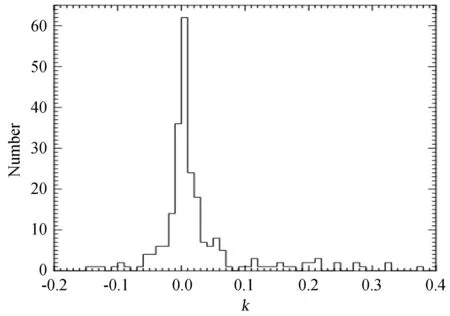
图6 185个伽玛暴的k分布图

4 结论和讨论

光变曲线是目前伽玛暴的最主要的观测资料，它有非常复杂的时间结构， 其变化很大， 没有任何两个暴具有完全相同的时间结构和能谱演化过程[14]。人们可以从光变曲线和能谱的一些研究中得出伽玛暴的一些性质，所以在过去的研究中,人们对伽玛暴的光变曲线和能谱进行了大量的研究, 并试图解释这些伽玛暴光变曲线形状的形成以及伽玛暴的发射机理[15-18]；在这些研究中， 一般是通过统计分析或者结合对伽玛暴的时间分辨谱的分析来进行研究的，在今后的工作中，进一步研究伽玛射线暴的光变曲线和能谱的其他特性,从而深入揭示伽玛暴的辐射机制、伽玛暴产生的物理条件、内外激波的关系等问题。

[1]孙超, 刘琼, 毛竹, 等. Y射线暴光变曲线的研究[J]. 天文学报, 2008, 49(3): 267-272.

Sun Chao, Liu Qiong, Mao Zhu, et al. A study of variable light curves of GRB[J]. Acta Astronomica Sinica, 2008, 49(3): 267-272.

[2]Band D, Matteson J, Ford L, et al. BATSE observations of gamma-ray burst spectra. I: Spectral diversity[J]. The Astrophysical Journal, 1993, 413(1): 281-292.

[3]Katz J I. Low-frequency spectra of gamma-ray bursts[J].The Astrophysical Journal, 1994, 432(1): L107-L109.

[4]Tavani M. A shock emission model for gamma-ray bursts [J]. Physical Review Letters, 1996, 76(19): 3478-3481.

[5] Liang E W, Dai Z G, Wu X F, et al. The luminosity-ep relation within gamma-ray bursts and the implications for fireball models[J]. The Astrophysical Journal, 2004, 606(1): L29-L32.

[6]Amati L, Frontera F, Tavani M, et al. Intrinsic spectra and energetics of BeppoSAX gamma-ray bursts with known redshifts[J]. Astronomy and Astrophysics, 2002, 390: 81-89.

[7]Lloyd-Ronning N M, Ramirez-Ruiz E. On the spectral energy dependence of gamma-ray burst variability[J]. The Astrophysical Journal, 2002, 576(1): 101-106.

[8]Yonetoku D, Murakami T, Nakamura T, et al. Gamma-ray burst formation rate inferred from the spectral peak energy-peak luminosity relation[J]. The Astrophysical Journal, 2004, 609(3): 935-951.

[9]Sakamoto T, Lamb D Q, Graziani C, et al. High energy transient explorer 2 observations of the extremely soft X-ray flash XRF 020903[J]. The Astrophysical Journal, 2004, 602(2): 875-885.

[10]Lamb D Q, Ricker G R, Atteia J L, et al. Scientific highlights of the HETE-2 mission[J]. New Astronomy Reveviews, 2004, 48(5/6): 423-430.

[11]Zhang B, Mészáros Peter. An analysis of gamma-ray burst spectral break models[J]. The Astrophysical Journal, 2002, 581(4): 1236-1247.

[12]Preece R D, Briggs M S, Mallozzi R S, et al. The BATSE gamma-ray burst spectral catalog. I. high time resolution spectroscopy of bright bursts using high energy resolution data[J]. The Astrophysical Journal Supplement Series, 2000, 126(1): 19-36.

[13]Kaneko Y, Preece R D, Briggs M S, et al. The compete spectral catalog of bright BATSE gamma-ray bursts[J]. The Astrophysical Journal Supplement Series, 2006, 166(1): 298-340.

[14]陈海峰. Gamma暴光变曲线主峰特征参量的分布[J]. 广西民族学院学报, 2003, 9(2): 14-17.

Chen Haifeng. Distributions of the characteristics of the most intense pulses in gamma-ray burst light curves [J]. Journal of Guangxi University for Nationalities, 2003, 9(2): 14-17.

[15]Lee A, Bloom E D, Petrosian V. On the intrinsic and cosmological signatures in gamma-ray burst time profiles: time dilation[J]. The Astrophysical Journal Supplement Series, 2000, 131(1): 21-38.

[16]Kocevski D, Ryde F. Liang E. Search for relativistic curvature effects in gamma-ray burst pulses[J]. The Astrophysical Journal, 2003, 596(1): 389-400.

[17]Ryde F. The cooling behavior of thermal pulses in gamma-ray bursts[J]. The Astrophysical Journal, 2004, 614(2): 827-846.

[18]Qin Y P, Zhang Z B, Zhang F W, et al. Characteristics of profiles of gamma-ray burst pulses associated with the doppler effect of fireballs[J]. The Astrophysical Journal, 2005, 617(1): 439-460.