悬浮流中浮升气泡运动的数值模拟

彭小奇，陈思超，宋彦坡，刘 涛

(1.中南大学 能源科学与工程学院，长沙 410083；2.湖南第一师范学院 信息科学与工程系，长沙 410205)

泡沫浮选工艺被广泛应用于选矿生产。在浮选槽中，搅拌装置对矿浆进行激烈搅拌产生强烈的涡流，涡流的剪切作用使吸入浮选机的空气被分散成大量尺寸不等的气泡，这些气泡的初速度大多在0～0.1 m/s之间[1]。气泡在矿浆中运动时，矿粒与之碰撞并粘附于气泡表面，矿化后的气泡在浮选槽的静止区域中上升以减少矿粒的脱附[2]，矿粒随气泡上升至矿浆表面后，被收集成为浮选产品。显然，浮选生产的产量与产品质量与气泡运动密切相关，研究气泡在矿浆中的运动规律对改进生产过程、提高产品产量与质量具有重要意义。

由于气泡在液体中呈强非线性运动，运动过程中其界面变形较大，情况复杂多样[3]，难以通过解析方法具体分析其运动变化规律，故大多采用数值模拟方法进行分析研究。朱仁庆等[4]、武博等[5]和马斗[6]模拟得出了气泡在水中上升的运动速度随时间变化的规律，与气泡上升速度计算经验公式所得结果较吻合；KRISHNA等[7]运用VOF方法模拟了充满水的二维矩形域内单个气泡的上升过程，得到的气泡上升轨迹与实验观测结果基本一致；WU等[8]通过实验观察和理论分析方法获得了气泡的具体形成过程；LI等[9]也涉及了模拟气泡在非牛顿流体中的运动情况。上述国内外学者进行的大量理论和实验研究均是针对气泡在纯液体中的运动，对气泡在矿浆悬浮液中运动的模拟研究较少｡LUO等[10-11]先后通过实验研究了在高压液固悬浮体中气泡的生成与运动过程，提出了一种基于球对称假设的机理模型，对分析气泡在悬浮液中的受力情况作了一定的贡献；李彦鹏等[12]模拟了三维的液固悬浮液中气泡的上升，该研究很好地证明了气泡的上升会受到颗粒流的影响；李永强等[13]利用影像研究方法记录了气泡在旋流分选器中的运动现象，获得了对气泡运动规律的直观认识。在运用VOF方法方面，XU等[14]和SEONG等[15]证明了VOF方法模拟的结果与实际情况的一致性较好。

上述文献都使用不同研究方法成功地对气泡的形状、大小、轨迹等进行了定性的研究分析，但极少用到具体的数值去表示气泡变形的程度，研究浮选中气泡最佳尺寸的相关报道也甚少。由于气泡大小是浮选的重要表观特征之一，气泡过大或过小都直接影响着矿粒的回收率[16]，因此，本文作者在前面文献工作的基础及启发下，将VOF方法运用到简化的悬浮液中气泡运动的模拟上，在不同密度的静止均匀矿浆中的分离区，对不同初速度和不同初始直径下的单个气泡运动进行模拟，并使用气泡的具体形变参数对气泡在运动过程中形状、大小、轨迹等量的变化进行定量的分析，在不考虑气泡运载能力下，对浮选最佳升浮气泡尺寸范围进行研究，将模拟与研究分析结果与文献中已有的结果及实际生产情况进行比较。

1 气泡模拟的数值理论与方法

1.1 基本假设

本文主要研究气泡在浮选机分离区的运动情况。为便于研究，作以下假设：

因浮选槽中分离区矿浆的紊流程度较小，气泡进入分离区之后运动速度以垂直向上方向的速度为主[17]，且单个气泡在液-固悬浮流中的上升运动与其在高黏度流体中的运动类似，故将液固悬浮流视为静止的不可压缩的牛顿型均匀流体[18-19]；气泡初始形状为球形。

1.2 VOF方法

VOF方法[20-21]是一种通过追踪流场网格中流体体积变化来捕捉两相流运动界面的方法，其计算量小、精度高且容易实现。它定义每个网格中目标流体的体积与网格体积之比为C，即C是一个流体体积函数，由C的大小可知两相界面所处的位置：

体积函数C满足如下控制方程：

式中：t为时间变量，s；u为流体运动速度矢量，m/s。

1.3 气泡运动控制方程

因研究对象是一个等温系统的多相流系统，且气液两相流为不可压缩的牛顿流体，根据定义的VOF方法，可认为这个有相界面分隔的两相体系是单相流体系，故控制方程是对不可压缩流体的质量守恒方程和动量守恒方程[22]。

1) 质量守恒方程

2) 考虑表面张力的动量方程

式中：ρ为流体密度；u为流体的速度矢量；p为压强；Fs为表面张力源项；μ为动力粘性系数。

1.4 连续表面张力模型

本文研究气泡在矿浆中的运动考虑了表面张力的影响，在VOF模型中使用的表面张力，是通过散度原理表示为体积力，并采用了BRACKBILL等[23]提出的连续表面张力模型(Continuum surface force，CSF)将表面张力添加到动量方程中的源项。

定义αq为第q相体积分数，根据体积分数分布，可得界面法向矢量为

可得表面曲率为

式中：单位法向矢量为

则表面张力表示为

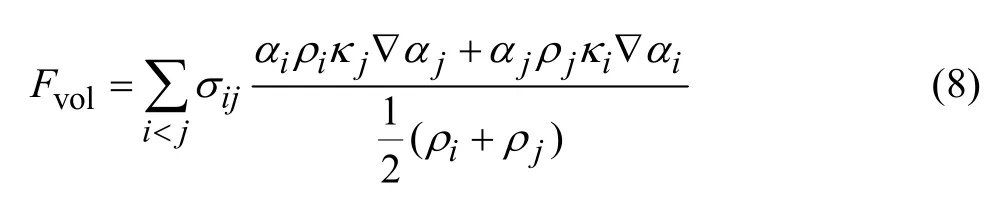
式中：i和j为单元中的i相和j相。若一个单元只有两相，则

式(8)即简化为

1.5 气泡运动过程中的形变参数

为更好的表达和说明气泡变形的程度，本文定义了以下3种参数，对气泡的形变从3个角度进行数值上的定量分析，具体表示如图1所示。

定义1：气泡晃动角θ，气泡在运动中变形后，其左右两顶点的连线与水平线的夹角定义为气泡晃动角，记为θ。晃动角的大小表明气泡在垂直方向上的晃动程度。在气泡上升过程中，其最大晃动角与最小晃动角代数差的绝对值U越大，则气泡晃动程度 越大。

定义2：气泡变形系数W，在运动中变形的气泡，其长轴与短轴之比定义为气泡变形系数，记为W。变形系数表明气泡外形上左右、上下伸缩的形变程度，即扁平程度，在气泡上升过程中，W越大，其变形程度越大。

定义3：气泡偏移系数M，变形的气泡中心与其初始气泡中心之间的水平方向距离与初始气泡半径之比定义为气泡偏移系数，记为M。偏移系数表明了气泡在上升过程中水平方向上的摆动幅度。M越大，则表明气泡上升运动轨迹的左右摆动幅度越大。

图1 气泡形变参数定义示意图Fig.1 Schematic diagrams of bubble deformation parameter definition: (a), (b) U=|θmax-θmin|; (c) W=b/a; (d) M=L/R

2 数值模拟结果与分析

2.1 初始边界条件和参数

为消除壁面带来的影响，当气泡直径D为7～8 mm时，取计算区域为0.04 m×0.1 m，其他直径取0.02 m×0.1 m的计算区域；采用四边形网格，网格间距等于2.5×10-4m，时间步长等于1.0×10-4s，顶部边界条件为压力出口，其他为无滑移壁面，矿浆处于静态，初始条件参数如表1所列。

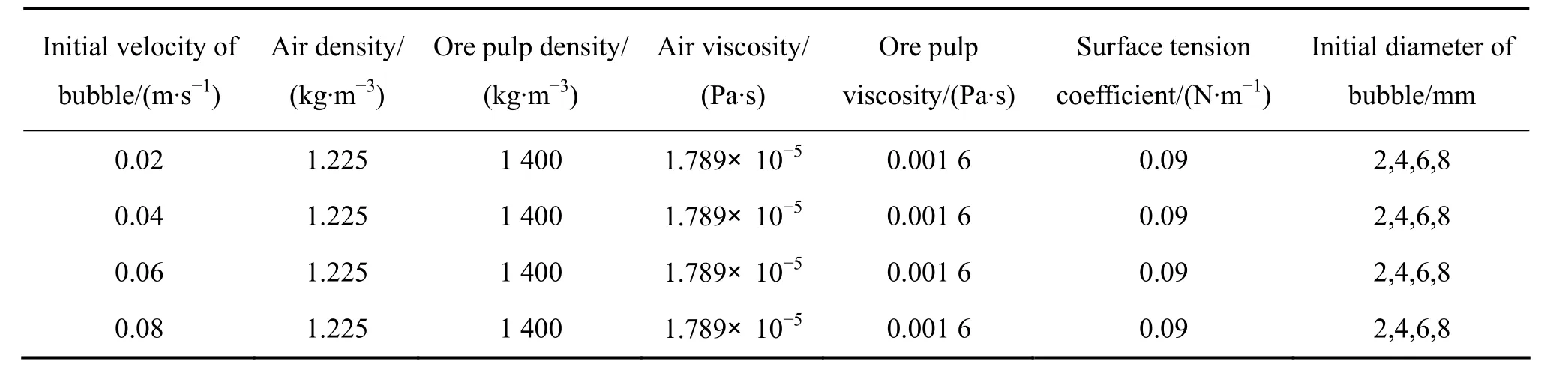
表1 浮升气泡运动数值模拟的初始条件参数Table1 Initial condition parameters for numerical simulation of flotation bubble motion

2.2 不同气泡直径对气泡上升的影响

同一初速度、不同初始直径的气泡运动轨迹、形变、上升速率等均不同。4种不同初始尺寸气泡在不同初速度时的运动轨迹如图2所示。由图2可见，气泡上升过程中该在形变和摆动，且变形和摆动的幅度随着初速度及初始直径的不同而各不相同。气泡在矿浆上升运动过程中因所受压力、浮力、阻力等的不均衡而该在变形、晃动等。

计算气泡初始直径为2和4 mm的晃动角θ均在0.5°以下，可忽略。其他形变参数值如表2所列。由此可知，气泡初始直径越大，其最大变形系数越大，最大偏移系数越小，即气泡的变形程度随其初始直径的增加而增大，其摆动幅度随气泡初始直径的增加而减少；同一尺寸的气泡初速度越大，其最大变形系数和最大偏移系数也越大，即气泡变形程度和摆动幅度随初速度的增加而增大；气泡晃动角随着气泡直径和初速度的增加而增大，即气泡初始直径和初速度越大，其在垂直方向上的晃动程度越大。

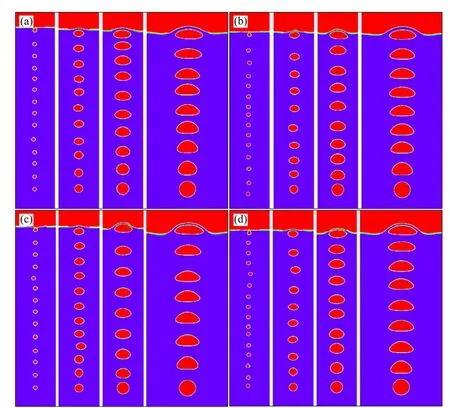
图2 不同尺寸气泡在不同初速度时的运动轨迹图Fig.2 Trajectory diagram of different size bubble in different initial velocities: (a) v0=0.02 m/s; (b) v0=0.04 m/s; v0=0.06 m/s;v0=0.08 m/s (From left to right, the bubble diameter is 2, 4, 6 and 8 mm, respectively.)

表2 不同初速度下不同初始直径气泡运动中的形变参数最大值Table2 Maximum bubble deformation parameter value with different bubble initial diameter under different initial velocity during bubble motion

由表2中数据可看出，直径为2 mm的气泡变形程度最小，但水平方向上的偏移幅度最大；直径为6和8 mm的气泡形变程度大，垂直方向晃动程度大。直径为4 mm的气泡形变过程较为平缓，与直径为2 mm的气泡相比，其水平方向上偏移幅度大幅度减小；由此可见，直径为4 mm的气泡形变情况最为理想。

2.3 不同初速度对气泡上升速度的影响

2.3.1 气泡运动初始阶段和稳定阶段的速度分布

不同直径的气泡在上升初始阶段和上升稳定后的速度矢量图总体上类似，由图3(a)可见，气泡在上升初始阶段，静止的矿浆受到的扰动使得气泡周围(液相)的速度场在左右两侧该在多个对称的涡结构，这些涡结构增加了气泡上浮的阻力和形变程度。由图3(b)可见，随着气泡的上升，液流速度场趋于稳定，气泡两侧形成了两个对称的涡结构，此时浮升力与液体压力及其他阻力基本达到平衡状态，气泡在此时形变较为平缓，上升速度平稳。

2.3.2 气泡运动速率变化规律

在不同初速度下，气泡在初始上升阶段整体上是加速运动的，但受不同直径气泡和不同初速度的影响，其加速阶段的具体加速过程有所不同，并呈现一定的规律，具体如图4(a)～(d)所示。

图4(a)所示为初速度为0.02 m/s时，4种直径的气泡上升初始阶段的速度—时间关系图。由图4(a)可以看出，4种直径气泡均是一开始上升便做加速运动，且直径为4 mm的气泡运动速度一直居首，这表明当初速度为0.02 m/s时，对液流的初始扰动较小，气泡所受浮升力均大于其所受的阻力，且直径为4 mm的气泡加速得最快。

图4(b)所示为初速度0.04 m/s时，4种直径的气泡开始上升到趋于稳定阶段的速度—时间关系图。由图4(b)可以看出，直径为4 mm的气泡运动规律是气泡一直做加速运动直至速度趋于稳定，且直径为4 mm的气泡运动速度大于其他直径气泡的运动速度；直径为2、6和8 mm的气泡运动规律是先减速，然后加速直至速度趋于平稳。

图4(c)和(d)所示的气泡运动规律与图4(b)的相同，这表明当该在由初速度为0.04、0.06和0.08 m/s引起的上浮阻力的情况下，直径为4 mm的气泡均能够克服扰动及其他阻力先进行加速运动；而直径为2、6和8 mm的气泡在较大初速度作用下，其浮升能力小于上浮阻力而首先作减速运动，之后随着上升运动阻力和液体压力的降低，运动速度逐渐增大直至稳定。

综合4种初速度下的气泡运动规律图可见，初始直径为4 mm的气泡抗液流扰动能力及初始阶段上浮速度较其他直径气泡的要大。

2.3.3 气泡该程运动时间

不同初速度情况下不同初始尺寸气泡该程运动的时间各不相同。由图5可见，同一初始直径气泡到达液面的时间总体上随着初速度的增加而缩短，4种气泡到达液面的先后顺序按直径排列为4、6、8和2 mm；直径为6 mm的气泡的平均速度略大于直径为8 mm的气泡的平均速度。v0= 0.02 m/s时，初始直径为6和8 mm的气泡由于在起始运动状态下阻力较小，初始阶段没有减速过程，该程运动时间长于其他初速度条件下的该程运动时间；v0= 0.04 m/s时，初始上升阶段的阻力较v0=0.02 m/s时的阻力大，初始直径为6和8 mm的气泡先减速了一段时间，因此，在该计算区域内，其上升时间长于初速度为0.02 m/s时的上升时间；v0为0.06和0.08 m/s时，虽然其上升初始阶段也该在较大阻力和一段时间的减速运动，但其减速完成并开始加速时的速度及其减速过程运动的路程较初速度为0.04 m/s时的大，因此，其运动时间较初速度为0.04 m/s时的要短。直径为2 mm的气泡由于浮升力最小，其平均上升速度最慢而最后到达液面。直径为4 mm的气泡在所有初速度情况下的该程运动时间最短，且随着初速度的增大，其上升至液面时间缩短，说明直径为4 mm的气泡上升平均速度最大，其上浮动力与上浮阻力之比大于其他直径气泡的上浮动力与上浮阻力之比，浮升能力最强。

图3 气泡上升速度矢量图Fig.3 Vector diagram of bubble rise velocity: (a) Initial stage; (b) Stabilization stage

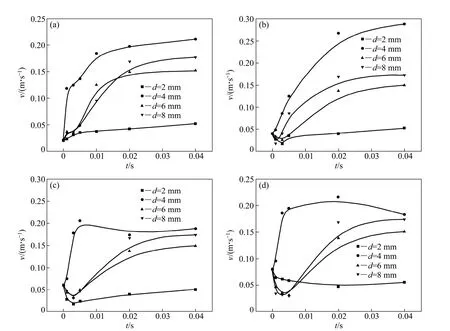
图4 不同直径气泡在不同初速度下0～0.04 s运动时间段的变化规律Fig.4 Change rule of different diameter bubble motions during 0-0.04 s at different initial velocities: (a) v0=0.02 m/s;(b) v0=0.04 m/s; (c) v0=0.06 m/s; (d) v0=0.08 m/s

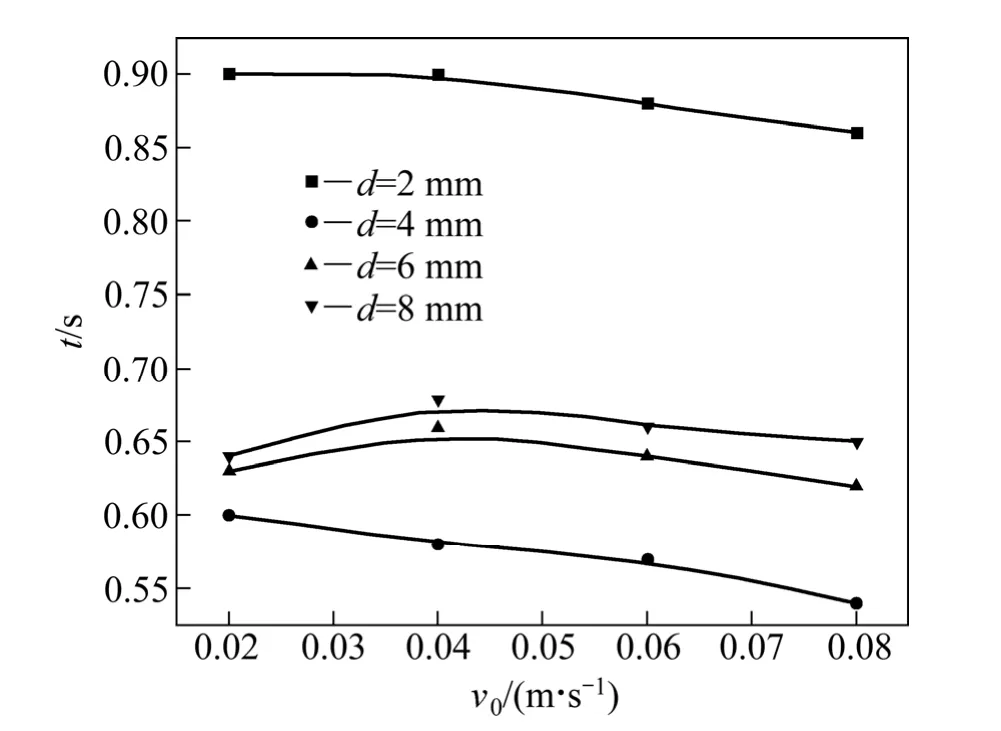
图5 不同初速度下不同直径气泡到达液面的时间Fig.5 Time of different diameter bubble reaching to liquid level at different initial velocities

气泡形变和扩张程度及摆动幅度越大，其表面粘附的矿粒越易脱落，气泡越易破灭；气泡初始直径过小，则其表面能粘附的矿粒尺寸及数量过小，气泡对矿粒的携载和输运能力随之变弱，两者均会导致浮选生产率降低，矿物回收率减少。综合 2.2～2.3节模拟结果及分析所述可知，初始直径为4 mm的气泡形变过程较为平缓，水平方向上偏移幅度较小，其浮升力与上升阻力之比较其他初始直径气泡的要大；在所有初速度情况下，其运动时间最短，即其上升平均速度最大，浮升能力最强，对矿粒的承载能力最强。因此，浮升气泡的尺寸以中等大小(直径为4 mm)为最佳。

2.3.4 气泡上升速度模拟计算与理论公式计算比较

对于单个气泡上升速度公式的推导有很多著名的公式，Stokes及Mendelson公式是其中之一，如式(12)所示，表示的是气泡上升平稳速度(u)与气泡直径的关系。

式中：ρf为流体密度，kg/m3；ρg为气体密度，kg/m3；CD为阻力系数；db为气泡的当量直径，m；g为重力加速度，m/s2。

气泡的上升过程可分为层流区、过渡区和紊流区3种情况。

1) 在层流区(Re＜1)时，则气泡上升速度公式为

式中：σ为表面张力系数，N/m。

2) 在过渡区(1＜Re＜300)时，气泡上升速度公式为

3) 在紊流区(300＜Re＜4 000)时，则气泡上升速度公式为

由式(13)、(14)和(15)可看出，当气泡上升处于层流区和过渡区时，气泡上升平稳速度与气泡直径大小成正比；当气泡处于紊流区时，气泡上浮平稳速度与气泡直径成反比。由于气泡在上浮过程中多处于过渡区和紊流区，因此，气泡在流体中的上升速度并不单纯地随着气泡直径的增大而增加。气泡的上升速度在运动了0.04～0.05 s之后就会达到一个平稳值，如图5所示，直径为4 mm的气泡上升平均速度最大，表明其上升平稳后的速度亦最大，与理论推导公式分析结果一致。在实际的气泡上升过程中，气泡很难达到力的平衡，且随着气泡的上升，其体积逐渐变大，造成阻力和浮升力出现非线性变化，此时气泡受力关系变得极其复杂。

3 不同矿浆密度对气泡运动的影响

3.1 不同密度矿浆中气泡的形变程度

本研究模拟3种不同矿浆密度下气泡上升的运动情况，其他条件不变。作为对比，增加了3种直径气泡的模拟实验，具体初始模拟参数如表3所列，模拟及计算结果如图6和表4所示。由图6可见，不同矿浆密度中，气泡上升过程中的形变情况及上升轨迹有所不同；由表4可知，气泡变形系数与矿浆密度成正比，气泡偏移系数与矿浆密度成反比，即气泡变形程度随矿浆密度的减少而减少，气泡上升轨迹水平方向上摆动幅度随矿浆密度的减少而增大；大气泡的偏角随矿浆密度的增大而减少，即矿浆密度越大,气泡在垂直方向上的摆动越小。

3.2 不同密度矿浆中气泡运动平均速度规律

不同初始直径气泡在不同密度矿浆中到达液面的时间各不相同，如图7所示。为比较新增初始直径气泡与原尺寸气泡的模拟结果，计算矿浆密度为1 175 kg/m3、气泡初始直径为4、5、6、7 mm的各种形变参数及矿浆密度为1 600 kg/m3、气泡初始直径为3、4、5、6 mm的各种形变参数，计算结果如表5和6所列。

由图7可见，矿浆密度越大，气泡到达液面所需时间越长，表明气泡随着矿浆密度的增大受到的黏滞阻力越大，气泡上升的平均速度越小。由表5可知，在矿浆密度为1 175 kg/m3时，直径为5 mm的气泡的偏移系数最大值(0.122)小于直径为4 mm的气泡的偏移系数最大值(0.251)。同时，由图7可见，直径为5 mm的气泡到达液面所需的时间比直径为4 mm的气泡所需的时间要少，即其上升的平均速度更大，所以在矿浆密度为1 175 kg/m3时，最佳浮升气泡尺寸在5 mm左右。由表6可见，在矿浆密度为1 600 kg/m3时，直径为3 mm的气泡的变形系数最大值(1.475)小于直径为4、5 mm的气泡的变形系数最大值，且直径为3 mm的气泡的晃动角(0.18)比直径为4 mm的气泡的晃动角(0.52)小，上升的平均速度略小于直径为4 mm的气泡的平均速度。综合各方面情况可见，在矿浆密度为1 600 kg/m3时，最佳浮升气泡趋于初始直径为3 mm左右的气泡。

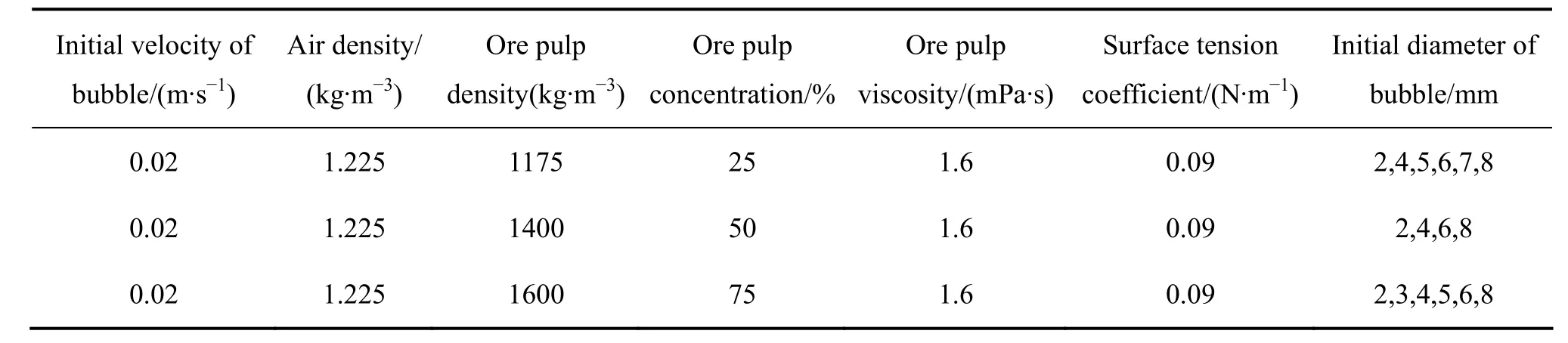
表3 在不同密度矿浆中模拟的初始条件参数Table3 Initial condition parameters of simulation in different ore pulp densities

图6 不同矿浆密度中气泡的运动规律Fig.6 Bubble motion law in different ore pulp density: (a) 1 175 kg/m3; (b) 1 400 kg/m3; (c) 1 600 kg/m3; (d) From left to right:D=3 mm, ρ=1 600 kg/m3; D=5 mm, ρ=1175 kg/m3; D=5 mm, ρ=1 600 kg/m3; D=7 mm, ρ=1175 kg/m3

表4 不同密度下不同初始直径气泡运动中的形变参数最大值Table4 Maximum bubble deformation parameter value with different bubble initial diameters in different densities during bubble motion

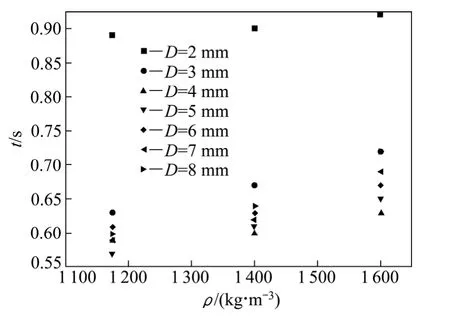
图7 不同矿浆密度下不同初始直径气泡到达液面的时间Fig.7 Time of different diameter bubble reaching to liquid level under different pulp densities

综上模拟结果及分析可知：矿浆密度为1 175 kg/m3时，最佳浮升气泡尺寸在5 mm左右；矿浆密度为1 400 kg/m3时，最佳浮升气泡尺寸在4 mm左右；矿浆密度为1 600 kg/m3时，最佳浮升气泡尺寸在3 mm左右。因此，在不同密度的矿浆中，最佳浮升气泡初始尺寸各不相同。

表5 矿浆密度1 175 kg/m3下气泡形变最大参数值Table5 Maximum bubble deformation parameter values in density of 1 175 kg/m3

表6 矿浆密度1 600 kg/m3下气泡形变参数值Table6 Maximum bubble deformation parameter values in density of 1 600 kg/m3

在实际生产中，矿浆含量在25%～50%之间，对应的矿浆密度为1 175～1 400 kg/m3，因此，通常情况下，中等尺寸(直径为3～4 mm)的浮升气泡可获得较好的浮选生产效果。

4 结论

1) 运用VOF方法对不同初始直径、不同初速度条件下的气泡在3种不同密度的矿浆中的运动情况进行了模拟实验，得到了气泡的运动轨迹和速度分布图，并计算了气泡形变最大参数值。

2) 在矿浆密度为1 400 kg/m3时，直径为4 mm的气泡相比其他气泡形变平缓，上升速度最大，浮升能力最强，最有利于矿粒的回收；矿浆密度有所偏大或偏小时，浮升气泡的最佳尺寸仍为3～5 mm。这证明了气泡尺寸过大或过小时，其运动形变情况均不利于矿粒的回收，该模拟结果与实际生产情况高度吻合。

3) 对模拟结果的分析表明：当气泡初速度v0=0.02 m/s时，气泡在上升初始阶段受到液流的扰动影响不大；当气泡初速度v0＞0.02 m/s时，气泡受到的初始上浮阻力较大。

4) 实验结果证明，与实际生产中的矿浆浓度对应的最佳浮升气泡尺寸为3～4 mm。

[1]选矿机械设备实用手册.第六篇.浮选机械设备[J].北京: 机械工业出版社, 1994: 617-621.Practical manual of mineral processing mechanical equipment.Sixth part.Flotation mechanical equipment[J].Beijing: Chinese Machine Press, 1994: 617-621.

[2]韩 伟.浮选机内多相流动特性及浮选动力学性能的数值研究[D].兰州：兰州理工大学, 2009: 9-12.HAN Wei.The numerical research of multiphase flow characteristics and flotation dynamics performance in flotation machine[D].Lanzhou: Lanzhou University of Technology, 2009:9-12.

[3]PETER L, FRANZ P, NICOLAS F, PETER E.Gas bubble in simulation and experiment[J].Journal of Colloid and Interface Science, 2011, 354: 364-372.

[4]朱仁庆, 李晏丞, 倪永燕, 侯摇玲.气泡在水中上升运动的数值模拟[J].江苏科技大学学报: 自然科学版, 2010, 24(5): 2-3.ZHU Ren-qing, LI Yan-chen, NI Yong-yan, HOU Yao-ling.Numerical simulation of bubble rising in the water[J].Journal of Jiangsu University of Science and Technology: Natural Science Edition, 2010, 24(5): 2-3.

[5]武 博, 郝宗睿, 陈 涛, 吴大转.水下气泡运动的数值模拟[J].科技论文在线, 2010, 5(8): 2-4.WU Bo, HAO Zong-rui, CHEN Tao, WU Da-zhuan.Numerical simulation on motion of bubble under water[J].Science Paper Online, 2010, 5(8): 2-4.

[6]马 斗.单孔气泡动力学行为的VOF数值模拟[D].天津: 天津大学, 2009: 37-43.MA Dou.Numerical simulation of single orifice gas bubble motion behavior with volume of fluid method [D].Tianjin:Tianjin University, 2009: 37-43.

[7]KRISHNA R, van BATEN J M.Rise Characteristics of Gas Bubbles in a 2D Rectangular column: VOF simulation vs experiments[J].International Communications in Heat Mass Transfer, 1999, 26(7): 965-970.

[8]WU Rui-zhi, SHU Da, SUN Bao-de, WANG Jun, LU Yan-ling.Observation and theoretic analysis of gas-bubble formation and growth in water-model[J].Transactions of Nonferrous Metals Society of China, 2005, 15(5): 1130-1131.

[9]LI Zhang, CHAO Yang, CAO Zai-sha.Numerical simulation of a bubble rising in shear-thinning fluids[J].Journal of Non-Newtonian Fluid Mechanics, 2010, 165(11/12): 555-561.

[10]LUO X, YANG G Q, LEE D J.Single bubble formation in high pressure liquid-solid suspensions[J].Powder Technology, 1998,100(2/3): 103-108.

[11]YANG G Q, LUO X, LAU R.Bubble formation in high pressure liquid-solid suspensions with plenum pressure fluctuation[J].AICHE J, 2000, 46: 2163-2168.

[12]李彦鹏, 张乾隆.液固悬浮液中气泡生成的数值模拟[J].水动力学研究与进展, 2007, 22(4): 457-462.LI Yan-peng, ZHANG Qian-long.Numerical simulation of bubble formation in liquid-solid suspensions[J].Journal of Hydrodynamics, 2007, 22(4): 457-462.

[13]李永强, 李长根.旋流闪速浮选法的研究Ⅱ: 旋流分选器中气泡的运动规律[J].有色金属, 2000, 52(2): 22-23.LI Yong-qiang, LI Chang-gen.Study on cyclone flash flotationⅡ: Study on movement pattern of air bubbles in separation cyclone for cyclone flash flotation[J].Nonferrous Metals, 2000, 52(2): 22-23.

[14]XU Ling-jun, CHEN Gang, SHAO Jian-bin.Numerical simulation of bubble behavior using VOF method[J].Electric Technology and Civil Engineering, 2011, 22(24): 2408-2410.

[15]SEONG S J, SEONG J K, GOON C P.CFD simulation of condensing vapor bubble using VOF method[J].World Academy of Science, Engineering and Technology, 2009, 60(36): 1-6.

[16]龚明光.泡沫浮选[J].北京: 冶金工业出版社, 2008: 108-110.GONG Ming-guang.Froth flotation[J].Beijing: Metallurgical Industry Press, 2008: 108-110.

[17]曾克文.浮选槽内矿浆紊流强度对浮选影响的理论及应用研究[D].长沙:中南大学, 2001: 51-53.ZENG Ke-wen.Theory and application study on the effect of pulp turbulence degree in flotation cell on flotation[D].Changsha: Central South University, 2001: 51-53.

[18]YANG G Q, BING D U, FAN L S, Bubble formation and dynamics in gas-liquid-solid fluidization-A review[J].Journal of Chemical and Biomolecular Engineering, 2007, 62(1/2): 2-5.

[19]HUA J S, STENE J F, LIN P.Numerical simulation of 3D bubbles rising in viscous liquids using a front tracking method[J].Journal of Computational Physics, 2008, 227(6): 3358-3382.

[20]ZHANG Yu-jie, LIU Ming-yan, XU Yong-gui, TANG Can.Three-dimensional volume of fluid simulations on bubble formation and dynamics in bubble columns[J].Chemical Engineering Science, 2012, 73(7): 55-78.

[21]MA Dou, LIU Ming-yan, ZU Yong-gui, TANG Can.Two-dimensional volume of fluid simulation studies on single bubble formation and dynamics in bubble columns[J].Chemical Engineering Science, 2012, 72(16): 61-75.

[22]徐玲君, 陈 刚, 邵建斌, 薛 阳.单个气泡静水中上升特性的数值模拟[J].沈阳农业大学学报, 2012, 43(3): 357-361.XU Ling-jun, CHEN Gang, SHAO Jian-bin, XUE Yang.Numerical simulation of motion behavior of single bubble rising in still water[J].Journal of Shenyang Agricultural University,2012, 43(3): 357-361.

[23]BRACKBILL J U, KOTHE D B, ZEMACH C.A continuum method for modeling surface tension[J].Journal of Computational Physics, 1992, 100: 335-354.