网络团购最优定价模型及策略研究

宁连举，冯 鑫，万志超

(北京邮电大学经济管理学院，北京100876)

0 前言

网络团购即互不认识的消费者团体借助“网络聚集的力量”来筹集资金向商家集体采购，以加大与商家谈判的筹码，获得最优的价格。国际通称B2T(business to team)，是继 B2B(business to business)，B2C(business to customer)，C2C(customer to customer)后的又一电子商务模式。近年来，随着互联网的蓬勃发展，电子商务市场稳步增长，其中团购市场发展势头不减。

在团购兴起的早期，绝大部分团购网站都采取了一种被称为团购拍卖 (group－buying auction，GBA)［1－3］的价格机制来进行团购销售活动。然而基于此种价格机制的第1批销售商家纷纷倒闭。对于这种现象，文献［4］从相关网站(如Mobshop)给出的产品销售清单入手分析，发现了积极参与的外部效应、价格跌落效应以及尾部效应，这些有关团购中消费者行为的实证研究无疑为研究GBA的分析模型打下了基础。文献［1］设计了一种基于确定需求曲线的假设分析模型来研究GBA的机理，分别比较了固定价格机制(fixed－pricing mechanism，FPM)与GBA价格机制在完全竞争和寡头垄断情况下的优劣。在此研究基础上，文献［2］分析了FPM与GBA 2种策略的优劣关系，发现在不考虑经济规模和商家偏好风险的情况下，FPM总是不会比GBA更差。

总体来说，在团购定价机制方面，以文献［1－8］为代表的学者，研究了不同在线团购模式的价格机制，并基于这些不同的价格机制提出了相应的团购营销策略。

定价策略是团购这种商业模式中的一个重要环节，国外学者对于商品的定价策略研究多数是基于动态定价机制，考察卖方应该如何定价，如何得出最优定价策略。Kincaid等［9］考虑了需求服从固定强度的泊松过程的连续时间模型，推导出价值函数的最优条件和最优价格。同时指出当顾客的保留价格和到达时间分布F为指数分布时，最优条件为Hamilton－Jacobi－Bellman(HJB)方程;Vakrat等［10］考察了同时使用网上拍卖和固定价格销售同质商品的情况。他们假定投标者人数是确定的且消费者充分了解价格信息，建立了一个单位物品拍卖的模型;Chen J等［2］研究了一种新型的基于Internet的动态价格机制—逢低买入，他们利用独立私有估价模型，分析了规模经济条件下商家采用逢低买入的盈利情况，对逢低买入与固定价格机制进行了比较。通过数值分析，给出了逢低买入优于固定价格机制的条件，指出逢低买入的适用环境。但是他们给出的计算逢低买入下卖方期望净收益的公式比较复杂，求解价格曲线的最优解较为困难。

本文借鉴Chen J等人的研究，结合目前国内团购的特点，提出了影响团购规模的加速因子的概念，着重分析了加速因子a、团购商品即时供给数量N这2个关键因素的变化对单个商家自身最优价格取值的影响，详细讨论了在不同N值的情况下，a的取值变化所引起的折扣因子d的变化规律，且进一步分析了国内完全竞争市场环境下，由于团购商品需求弹性的差别而引起的价格变化机制，并基于这些规律和机制提出了相应的定价策略。

1 FPM模型介绍

在团购市场上商家提供供给，并且决定价格曲线，此处不妨设价格曲线为一向量P，

(1)式中，Pi表示当购买商品数量为i时的单位价格。由于采用了FPM，所以P1=P2=…=Pn，即各个价格相等，若是GBA机制的话，则为P1≥P2≥…≥Pn。

根据Chen J［1］等人的研究，有如下团购规则和策略:

规则I:如果竞拍向量是 B=(b1，b2，…，bn)，n≤N，这时的交易价格为 p(B)=pq，q=Max(i|，这里H为0－1函数，即若x≥0，H(x)=1;若 x≤0，H(x)=0。

当交易价格为pq时，顾客出价不小于pq方能交易成功，成交价为pq。出价低于pq的顾客无法完成交易。

结合国内实际情况，国内绝大部分团购网站均为 FPM，即 P=(p，p，…，p)，各单位货物价格均为p，顾客当且仅当出价p即可完成交易。

策略S:若潜在顾客对团购商品的估价为v，设其购买函数为V(P)

(2)式中:“0”表示潜在顾客没有拍下货物或者拍下后没有付款;pj为(1)式价格向量中的分量，当顾客估价v位于2个分量之间时，则取较小值。S策略表明当pN高于潜在客户内心估价时，潜在顾客会放弃购买。反之，潜在顾客会购买该产品。

根据规则I和策略S，产品的总销售量为

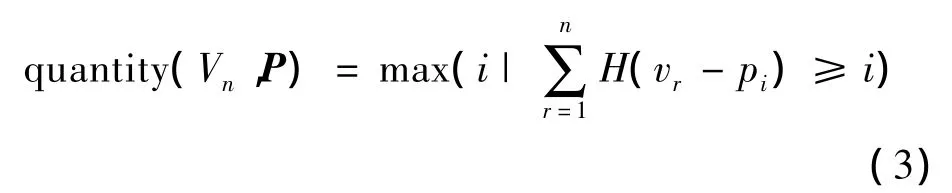
(3)式中，Vn=(v1，v2，…，vn)表示 n 个潜在顾客对商品的内心估价，其中vj(j=1，2，…，n)表示第j个潜在顾客的估价。商家的收益表示为

(4)式中:Pquantity表示交易价格;Vn表示n个顾客对商品的估价;C为单位商品成本。

由上述规则得如下商家收益的表达式为

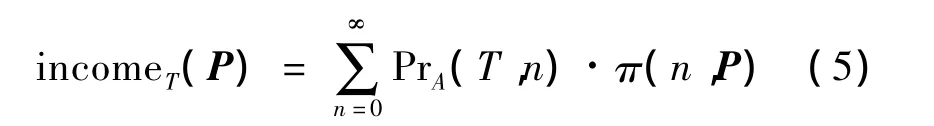
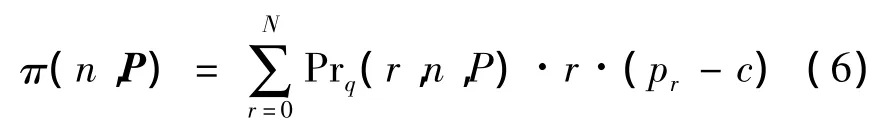
(6)式中，Prq(r，n，P)表示 n个客户中有 r个购买的概率，P为商品价格。

2 模型假设及建立

基于上述讨论，结合国内团购网站的实际情况，本文将从商家角度出发，建立团购商品的定价模型，找出最优定价方案及相关的营销策略。

2.1 具体模型假设

1)访问团购网站的顾客随机到达且服从某种随机过程，其到达和购买的时间间隔可忽略。本文实际算例采用泊松过程。

2)到达的顾客是理性的，风险偏好为中性。

3)每个潜在顾客对团购商品的估价为一个独立同分布的随机变量，与他人估价无关，本文采用正态分布。

4)为了便于计算及与同类型商品的比较，潜在顾客对团购商品的估价用折扣来表示而非绝对金钱数量。

5)每个潜在顾客的需求数量为1［3］。实际情况中可能出现一些顾客需求量为n的情况，此时可视为n个需求量为1的顾客到达即可。

6)潜在顾客到达的速率由2部分组成，一部分由网站稳定的访问速率构成，另一部分由商品价格本身和团购网站营销等外部因素所引起的速率变化组成，速率变化有正有负，分别表示团购网站的运营状况好与坏。由于本文立足于国内团购网站蓬勃发展的现状，故而只讨论速率变化为正的情况。

2.2 商家的预期收益模型

根据FPM的理论基础和上述的模型假设，为了便于讨论问题和减少运算量，我们设产品的成本价格C为常数，即成本价格变化不大，同时令C=0，即先不考虑成本，在求解的最后，用所得最优解P－C即可得每单位商品所得的利润，再乘以所买产品数量即可得总利润。

将假设带入(5)式中，经过整理后得如下函数:

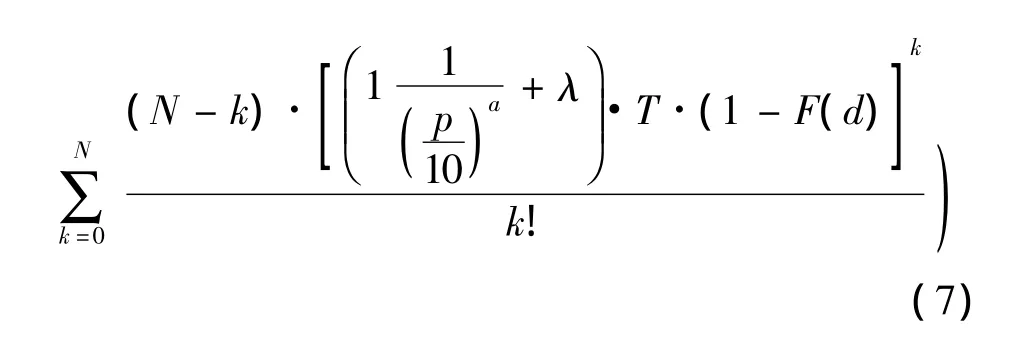
商家预期收益模型中相关参数介绍。

1)加速因子a(accelerator)。a为网站客流量的加速因子，其大小与固有客流量λ正相关。此外a还与团购网站本身的近期广告、促销活动等营销策略有关，营销活动越积极，a值越大。本文中的取值受到计算精度和实际数据等因素的限制一般不超过2.5。通常，在其他条件不变的情况下，商家的收益曲线是加速因子的单调增函数，但是当营销出现问题或者服务出现问题(如存在欺诈、送货延迟等情况)时会出现相反的效果。考虑到国内团购网站的良好发展情况，故在此只讨论商家的收益曲线是加速因子的单调增函数的情况。

2)固有客流量λ。λ为相关团购网站的固有客流量，一般设为大于零的定值。在其他条件不变时，收益曲线是λ的单调增函数。长期来看，随着团购网站的不断发展，λ将越来越大。

3)商品储备量N。N和加速因子a的不同组合对于商家的最优定价点有重要影响。当团购产品为实体商品时，N为有限正整数;当团购商品为服务类商品(表现为优惠券、代金券等票据形式)，则N为无限大的正整数，其取值可参考网站平均访问量，一般取一个远大于平均访问量的正整数来计算即可，将无限问题化有限问题。

4)折扣因子d。在其它条件不变时，收益曲线是折扣因子d的凸函数，d取值为(0，10)。

5)团购持续时间T。在其他条件不变的情况下，商家的收益曲线是团购的持续时间T的单调增函数，其取值范围为(0，+∞)，取零也可以，但是没有意义，故而去掉“0”这个点。

6)消费者估价偏好分布函数F(d)。此函数用以描述某一群消费者对于某种商品的价格偏好的分布情况，其中分布函数的期望是群体价格偏好的均值，方差用以描述个体价格偏好的离散程度。关于消费者价格偏好的真实分布情况可由各团购网站自身历史数据分析得出。本文中为方便计算，取正态分布来描述消费者价格偏好。

本文的重点讨论对象为加速因子a、商品储备量N的变动对于折扣因子d最优解变动的影响和此影响背后所隐藏的经济规律，以及如何运用所揭示的经济规律来调整营销策略、管理团购网站运营。

3 模型参数分析

本文运用Mathematica软件将定价模型的表达式(7)式转化为对应的编程语言进行相关的数值分析，着重探讨了加速因子a在商品储备量N的变动情况下对商家最优定价点的影响。

由上述参数介绍可看出1/(d/10)a+λ即为当前团购网站的顾客流量。从模型中不难看出1/(d/10)a不仅与d相关，更与a相关，当a值较高时，可以直观地看出将会大大增加客流量，进而提高该网站的知名度、访问量和市场占有率，但是a对于商家最优定价点的影响则需要进一步讨论。

首先我们假设团购产品的数量N=40，团购持续时间T=100 h，固有客流量λ=0.3，消费者价格偏好分布函数为μ=5，σ=1的正态分布时，a的变动对商家的收益的影响。(a，0，1.2，0.3)表示 a 从0开始以0.3的步长增长到1.2，这时用 Mathematica来绘制折扣-收益的商家收益曲线，其中横轴为商品的折扣，纵轴为总收入。分别取a=0，1.2时所得折扣-收入图形如图1所示。

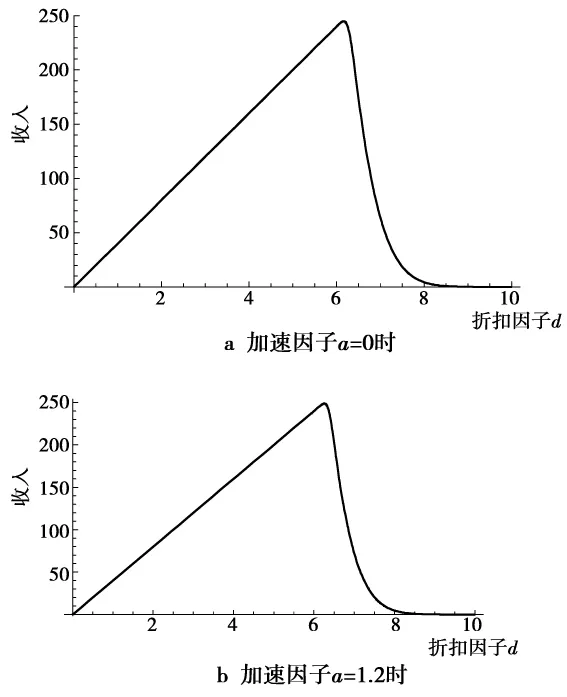
图1 N=40时，a=0和a=1.2时的折扣-收入曲线Fig.1 Discount－income curves of a=0 and a=1.2 with N=40

由图1a和图1b，很难看出区别，因为图形尺度较小，但是将a值按步长0.3递增由0变化到1.2时的5根曲线绘制到同一个坐标系中，其区别就比较明显了，如图2所示。

图2中，曲线的前半部分有较为明显的线性关系，是因为本例中N=40，取值较小。

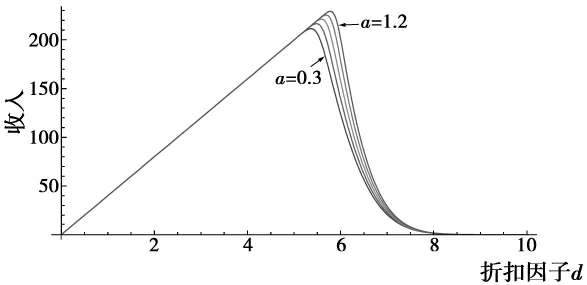
图2 N=40时，不同a值下的折扣-收入对比曲线Fig.2 Contrastive analysis of discount－income in different a values with N=40

由图2可知，当N=40时，随着加速因子的增大，收益曲线的最优值点向右侧移动，并且收入函数的最大值也在逐渐增加，只是幅度相对较小而已。通过计算，可以得出:当a=2.47时，收入的最优点为(242.7，p=6.1)，其中 p为归一化价格。当a=0时，收入的最优点为 (211.5，p=5.4)。

通过具体的数据我们发现，收入函数的最优解和最优值变化都不是很大。接下来讨论N=500的情况，其余条件同上。分别取a=0，1.2的折扣-收益曲线如图3所示。

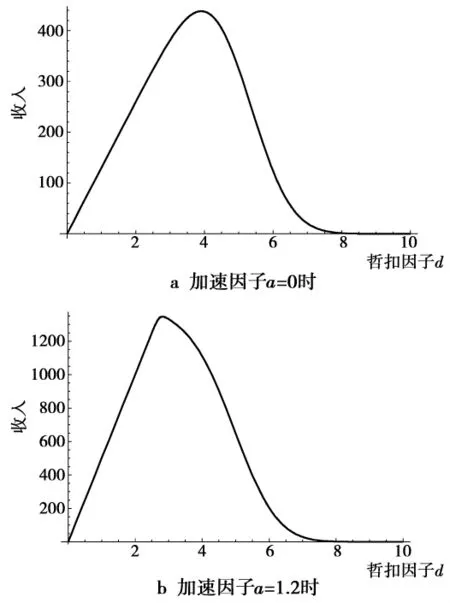
图3 N=500时，a=0和a=1.2的折扣-收入曲线Fig.3 Discount－income curves of a=0 and a=1.2 with N=500

图3a与图3b的区别比较明显，a=0时相对于a=1.2时曲线较为平缓，同时最优值远小于a=1.2的情形。同样，将a值按步长0.3递增由0变化到1.2时的5根曲线绘制到同一个坐标系中，曲线的变化将更为明显，如图4所示。

图4 N=500时，不同a值下的折扣-收入对比曲线Fig.4 Contrastive analysis of discount－income in different a values with N=500

由图4可知，随着加速因子 a的增加，收入(income)函数的最优解逐渐向左移动，最优值随着最优解的移动变化幅度较大。

对比图2和图4，看似存在矛盾，然而这2个看似矛盾的结论，恰恰解释了商品数量N和加速因子a对于团购商家收入影响的内在关系。

当N=40时，由于商品储备较少，可以认为现在是供小于求的卖方市场，这时候商家可以适当提高价格，然后再发起团购，但提高的幅度应该较小，一般不应高于一折。

如果商家的目的是为了做推广营销，这时就不应该提价，因为提价会导致1/(d/10)a变低，影响该商品品牌信息的传播速度，由于未提价所造成的收益损失则可以看作是广告成本。

而当N=500时，相对于本文中的数值分析数据来说，商品储备已经足够，这时可以认为是供过于求的买方市场，定价基于同类产品的历史销售情况。由图4不难看出如果以往同类产品的销售量只有贮备量N的1/4时，此时应该较以往降低1.5～2折的折扣，此时的定价最接近最优解。

通过追踪团购网站的数据发现:一般来讲，如果团购的是某种实体商品，N都不会太大，这时商家的定价策略可以根据卖方市场定价原则出发，结合本模型和网站历史数据进行计算，得出最佳定价方案;如果团购的是某种服务类商品，如:餐饮代金券、电影票、旅游景点门票等，这时可视为买方市场，结合历史数据考虑降价0～2折销售该产品。

4 完全竞争市场中的定价策略

经过上述的模型讨论与分析，不难看出对于加速因子a和商品数量N的不同组合，“价格”的制定对团购商家的收益冲击很大，因此本节将从网络营销的观点来讨论商家的定价策略。

从目前的市场情况来看，国内团购市场目前还是一个完全竞争的市场，尚有数十家知名团购网站共存竞争。从传统的经济学角度来看，如果一个市场是完全竞争市场，则厂商是价格的接受者。然而团购不同于一般的市场，它有自身的特点，首先团购有较强的品牌和口碑效应，其次不同团购商家的进货渠道存在较大差异，所以，团购商家在某种意义上就掌握了一定程度的团购定价主动权，当然这种主动权是基于历史销售情况和市场情况的。

接下来我们从经济学的角度结合本文所提出的模型来分析相关的定价策略。

在经济学的定义中，需求弹性定义为

(8)式中:P为价格(price);Q为数量(quantity);TR为总收入(total revenue)。具体到本模型中，由于收入函数完全可以看作P和d(discount)的函数，即income=P×d，其中，对income函数上任意一点求导，经整理后得:

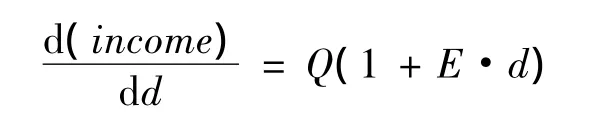
因此，不必画出整条income曲线，而只需取到2个相邻比较近的点就可以估算出该点的需求弹性系数E。通过需求弹性系数E和加速因子a我们就可以制定相关的竞争定价策略。

这里，以团购商家甲和乙为例来分析他们该采取何种定价策略。设甲和乙的需求弹性系数分别为E1，E2，加速因子分别为 a1，a2，其他指标相当，且初始定价和成本相同。

当a1≥a2时，说明甲的近期营销状况积极，当甲实施降价策略时，能吸引更多的客流量，反之则说明乙能吸引更多的客流量。此时，若E1＞E2＞1，说明甲和乙分别组织的团购商品都富有弹性，双方都应该降价，只不过甲比乙更具有竞争力，甲将获得更多的收益。此时甲的营销策略无论是从利润导向、销售额导向抑或市场占有率导向来说，甲都应该降价，且降价幅度甲应该向乙看齐，而不是直接降价到E1=1的点，因为E1=1的点在实际经济活动中并不易找到。此时，甲只要一直盯紧乙的定价策略即可;而对于乙来说的，因为a1≥a2的缘故，乙的降价幅度必须要比甲更多，才能更具竞争优势，但是降价的下限是E2=1时所取的折扣。从长期来看，在a1≥a2的条件不变的情况下，最后的结果应该是双方分别在E1=E2=1的点分别定价;但是也有可能出现a1≥a2假定条件改变的情况，比如乙在某种程度上比甲更了解市场需求，能尽可能早地调整定价策略，使得在一个较长的时间段内，乙的客流量比甲大，经过这段时间后有可能造成乙的固有客流量λ相对于甲有较大优势，进而使得双方加速因子的大小关系发生变化

如果E1＞1＞E2，则说明乙关于此类团购商品的竞争力同甲相比有较大差距，处于劣势地位，应该考虑放弃此类商品的团购业务，或者加强营销投入，提高自身的加速因子以弥补竞争劣势。

如果1＞E1＞E2，则说明甲和乙关于此类团购商品的经营都存在劣势，只不过甲比乙情况稍好而已，此种情况下，双方都可以通过积极的营销活动和及时的价格调整等手段来相互竞争，争夺市场。当然也可以果断的放弃处于劣势的团购商品市场，将更多的资源投入己方的优势市场以取得支配地位。

5 结论

团购商品最优定价策略一直是网络团购中的重要问题，也正在成为国内外学者的研究热点。本文通过提出基于FPM机制的团购商品最优定价模型，对网络团购定价策略进行了研究。由本文的模型和策略分析可知，影响网络团购商家定价的因素主要有3个:加速因子a、商品供给数量N和需求弹性系数E，并分2个阶段对定价策略进行分析研究。

在第1阶段分析中，从单个团购商家自身发展的角度来分析其定价策略，不涉及到竞争，主要涉及加速因子和商品供给数量这两方面，加速因子用以描述商家的营销状况，商品供给数量则用以描述商家对市场需求的认知程度，实际上涵盖了商品类型和商品数量，商品类型表明商家对消费者对某种团购商品的整体偏好程度，商品供给数量则表明商家对消费者关于此类商品需求的具体估计。

在第2阶段分析中，我们则在完全竞争的市场环境下分析了互为竞争对手的商家相互的定价策略，主要涉及到加速因子和需求弹性系数，二者的不同组合决定不同的定价策略。

随着网络团购市场蓬勃发展、产品愈趋同质化，“价格战”已成为团购的主要竞争手段之一。本文通过以上分析，总结出商家应该充分考虑自身的发展情况和市场环境，合理利用加速因子、商品供给数量和需求弹性系数来制定合理营销策略，以期实现企业自身的营销目标。

［1］ANAND K S，ARON R.Group buying on the web:A comparison of price－discovery mechanisms ［J］.Management Science，2003，59(4):1546－1562.

［2］CHEN J，CHEN X，KAUFFMAN R J，et al.Should we collude?Analyzing the benefits of bidder cooperation in online group－buying auctions［J］.Electronic Commerce Research and Applications，2009(8):191－202.

［3］王欢，张利，叶柯柯.大学生网络团购面临的问题及对策研究［J］.重庆邮电大学学报:社会科学版，2012，24(5):102－106.WANG Huan，ZHANG Li，YE Keke.Problems and Strategies of Group Purchase Online College Students Confront［J］.Journal of Posts and Telecommunications:Social Science Edition，2012，24(5):102－106.

［4］KAUFFMAN R J，WANG B.New buyers’arrival under dynamic pricing market microstructure:the case of groupbuying discounts on the Internet［J］.Journal of Management Information Systems，2001，18(2):157－188.

［5］HSIEH F S，JIM B L.Assessing the benefits of groupbuying－based combinatorial reverse auctions［J］.Electronic Commerce Research and Applications，2013(9):407－419.

［6］ZHOU G，XU K Q，STEPHEN S Y.Do starting and ending effects in?xed－price group－buying differ? ［J］.E－lectronic Commerce Research and Applications，2013，12(2):78－89.

［7］KAUFFMAN R J，LAI H，HO C T.Incentive mechanisms，fairness and participation in online group－buying auctions［J］.Electronic Commerce Research and Applications，2010，9(3):249－262.

［8］KAUFFMAN R J，LAI H，LIN H C.Consumer adoption of group－buying auctions:an experimental study［J］.Information Technology and Management，2010，11(4):191－211.

［9］KINCAID W M，DARLING D A.An inventory pricing problem［J］.Math Ananlysis Application，1963，7:183－300.

［10］VAKRAT Y，SEIDMANN A.Can online auctions beat online catalogs? ［C］//Proceedings of the Twentieth International Conference on Information Systems(ICIS).Charlotte，North Carolina:ACM，1999:132－143.