粘滑过程中的多点错动

李普春 刘力强 郭玲莉 刘培洵

(中国地震局地质研究所，地震动力学国家重点实验室，北京 100029)

0 引言

地壳运动在不同的时空尺度上都是不均匀的，大到地质历史上的造山运动，小到一条断层的位移。地震是地壳运动的一种形式，其震源过程在时空上也是不均匀的。然而，在关于震源过程的早期描述上，由于观测密度不够，为了便于处理选择了比较简单的力学模型。因此，早期许多地震学的理论或方法建立在单震源或者点源模型之上，在此基础上提出了一整套经典的震源理论(Aki，1966;陈运泰等，1992)，包括从最初的弹性回跳理论到后续的位错模型、点源单力偶模型和双力偶模型等。20世纪80年代学者开始注意到一次地震包含多点位错的现象(Snay et al.，1985)。最近10多年来，通过高密度宽频带台网对许多地震的观测发现，一些大地震并非只由一个震源引起，在地震的瞬间可能有多个震源存在(Jones et al.，1997;马超等，2006)。例如，汶川地震就曾经被拆解为多个顺序发生的次级地震(张勇等，2008，2009;杜海林等，2009)。但这种现象多见于大地震，而在小地震过程中由于破裂尺度小于地震波的波长，观测到多震源的报告并不多见。

实验室中的粘滑实验研究中也曾经利用声发射(Acoustic Emission，以下简称AE)波数据对声发射源进行过研究，并取得了一些成果。例如定位、震源机制解(Lockner et al.，1977;陈颙，1977;Sondergeld et al.，1982;陈颙等，1990;雷兴林等，1991;Lockner，1993;马文涛等，1995a，b;Hardy，1999;刘力强等，1999;蒋海昆，2000;刘培洵等，2007;Grosse et al.，2008;Ben-David et al.，2010)等等。与天然地震研究的基本物理模型类似，这些工作大多数也都是基于单震源位错模型对观测数据进行处理。即使是与天然小地震相比，实验室粘滑事件的尺度还是小得多。那么在实验室尺度上的粘滑事件可能存在类似于天然大地震的多震源或多点位错现象吗?由于野外很难预知地震断层，因此难以在地震时进行沿断层的极近场观测。在实验室条件下，从样品上预制的断层附近直接观测获得粘滑过程中的多点位错现象则是完全可能的。

由于多点滑动本质上是力学场的复杂性决定的，而AE仅仅是振动信号，还难以标定，因此其力学意义不够明确。要研究多点震源问题，首先要能够观测瞬时变化的复杂力学场，但需要有较高性能的观测系统。在以往的一些研究中(雷兴林，1995;马文涛等，1995a，b;邓志辉等，1995;蒋海昆，2000)，由于当时技术条件的限制，系统的观测能力比较低，尤其是应变记录仪的采样频率较低，稳定状态下的采样频率仅为20～50Hz左右，而且其信噪比也不高，难以记录更多关于粘滑失稳事件瞬间的数据资料。随着技术的进步，刘力强、郭玲莉等2011年完成对中频应变系统的研制开发，其采样频率大大提高到3.5kHz左右，可以捕获更多断层失稳的瞬态数据，能够提供更多断层失稳瞬时变化的力学场，尤其为研究多点震源错动时将声发射场与瞬态应变应力场之间进行对比提供了可能(GUO et al.，2013)。

本文从声发射和应变场这两方面进行分析。在声发射方面，包括对粘滑事件的定位，近场声发射波的初动方位空间分布，在应变场方面，主要从应变的分布情况，快速滑动时的应变振荡频率和失稳瞬间应变增量初动方位空间分布等，来分析粘滑过程中震源多点错动的现象。

1 实验条件

实验中使用一台多通道声发射仪记录AE全波形数据。仪器设定参数为:16个信号通道，采样频率10MHz，一次触发波形的采样点数为4 096(对应采样时窗宽度为400ms)，系统死时间(刘力强，2003)约为10ms。该系统可记录到的AE频带大致为20～500kHz，对应声发射波长大致为几个mm至上百mm范围，最大振幅为±1v，噪声水平为0.5mv。由于本次实验是对粘滑期间的大应力降事件进行研究，希望仅仅记录能量较大的AE事件，因此将系统的增益设定得较低(100倍)，触发门槛值设定得较高(50%)，以尽量减少处理小能量事件造成的系统死时间。

本实验采用一套新研制的多通道高频应变仪记录粘滑应力降期间的瞬态应变场。该应变仪具有64个信号通道，应变分辨率约为1με，每个通道的采样频率均为3 400Hz，采用连续记录方式工作。在突发应力降的几百ms期间，利用本系统可以记录多点的瞬时应变变化过程，其采样间隔约为300μs，与AE的采样时窗大体相当，因此可以有效地与AE事件对比分析。

本次实验联合观测声发射和高频应变信号，2种传感器组成如图1所示的观测组，每组包含3个应变片与1个AE传感器。3个应变片A，B，C组成1个应变张量求解点，张量值用应变椭圆的最大主应变ε1、最小主应变ε2及其方位角θ来表示。从各个应变片所获得的观测值εA，εB，εC求解张量解的公式如下:

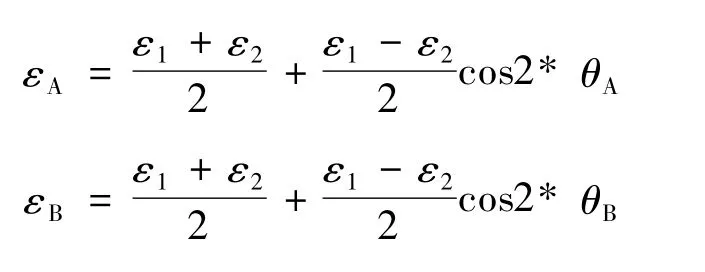
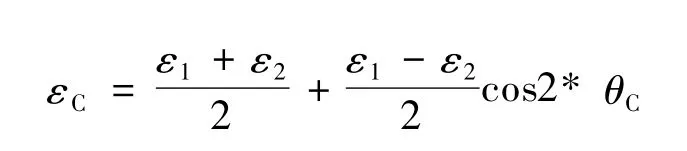
利用这个架构，在预制断层发生滑动所产生的高频振动被AE传感器所接收的时刻，可以获得其周边的瞬间应变场。

因而，目标达成度的“S-E-C-G”模型(S-student，E-expert，C-company，G-grade)为：

实验样品的材料为北京房山花岗闪长岩，规格为300mm×300mm×50mm，在对角线预制1条45°平直断层，形成简单剪切结构。本实验为了能在样品的预制断层附近进行直接观测，以获得可靠的数据，在样品上沿着预制切缝布置了12个上述观测组，共有12个声发射传感器和36个应变片组成。如图2所示。当然，单线布设的检波器并不利于初动辐射花样的监测和破裂位置定位。但是，如果认为在单剪粘滑实验中，失稳滑动主要是在断层上发生的，只需要在这种直线型布设的阵列中判断AE到时的先后以及波形初动的方向，就可以判断粘滑事件的起始位置。

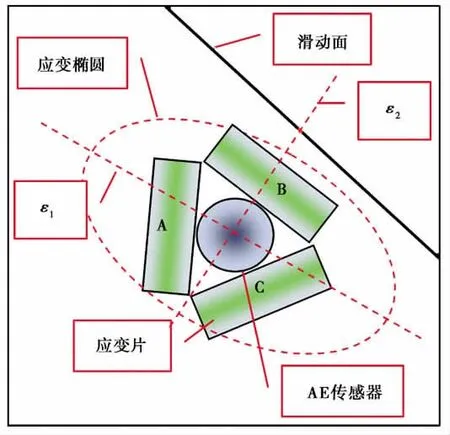
图1 声发射和应变片2组传感器组成图Fig.1 The AE sensor and strain sensor combination.

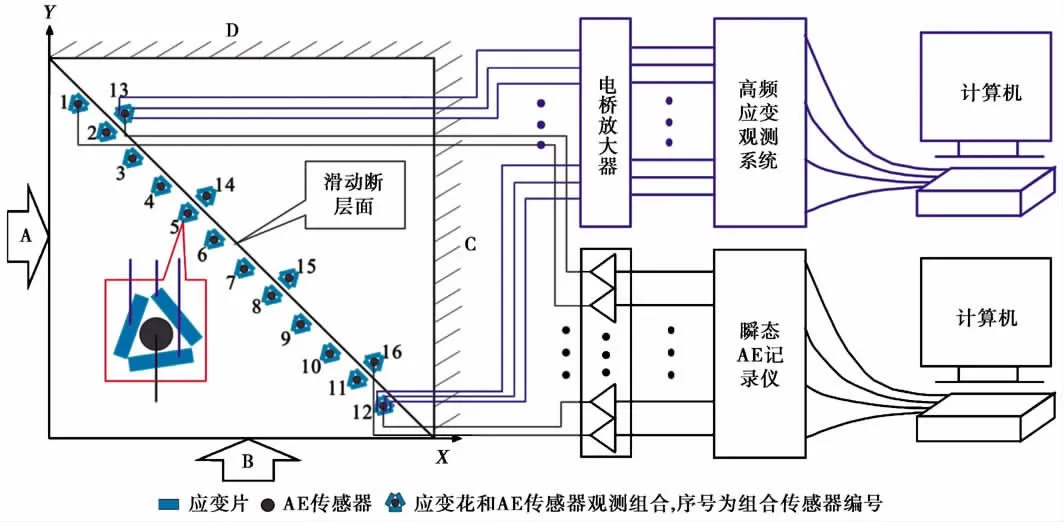
图2 实验样品和实验记录系统示意图Fig.2 The schematic illustration of sample and the experimental record system.

实验样品如图所示放置，其中C，D两侧为不动端，压机从A，B两侧向样品加载，A侧向右为X方向，B侧向上为Y方向。首先X、Y两个方向上都以同样的加载速率(0.8MPa/min)同步增长至10MPa。其后，保持X方向的压力稳定不变，Y方向以0.5μm/s的稳定位移速度给样品加载。其中，在3 810s和4 210s处Y轴的速率分别改成了1μm/s和0.2μm/s，在4 530s处又改成1μm/s。到5 135s时进入卸载阶段，最后完成实验，如图3所示。

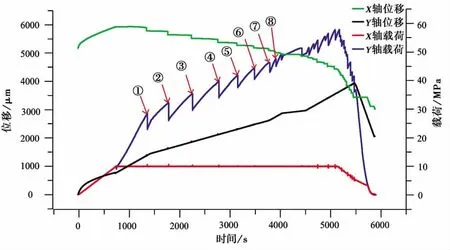
图3 实验加载位移曲线图Fig.3 The curve experimental of load vs.displacement.图中①为实验中粘滑失稳序号

2 实验结果

实验中，以一次明显的宏观应力降为一次粘滑失稳事件，每一次失稳事件中包含1次到3次明显应变值的快速变化，而每一次应变值的快速变化称为一个子事件，一个子事件一般对应产生1个AE事件(图4)。在实验中，共有26次粘滑失稳事件。其中，包含3个子事件的粘滑失稳事件有8次，包含2个子事件的粘滑失稳有8次，只有1个子事件的失稳事件有10个，在此选择其中部分事件进行详细分析与统计计算。

2.1 声发射

整体上看，由于在3 810s处改变了轴向加载速率，在3 810s以前的8次失稳粘滑事件中，除第1次事件外，每一个粘滑事件均对应着3个AE事件。在改变轴向加载速率以后的粘滑事件中，每次对应的AE事件个数多为2个，也存在单个的，其AE事件个数与加载速率有关。

在第2到第6次失稳滑动事件中，每次事件均包含3次AE事件，各次AE发生的间隔约为(100±15)ms，第1个和第2个AE事件之间的间隔明显长于第2个与第3个AE事件。从空间上看，3个成组事件中的每一个声发射分别被不同位置上的传感器最先接收，它们显然发生在断层的不同位置。但是也存在不同的情况，第7次和第8次失稳滑动事件产生的AE事件均被12号声发射传感器最先接收到，它们也可能发生于断层的同一位置。

以第3次失稳事件为例，分别对其包含的3次AE事件的到时定位和初动方位空间分布进行对比分析(第3次失稳事件对应的事件号为Event3，其包含的3个AE事件对应的事件号分别为 No.5，No.6，No.7，下文中没有特别指明时均同)。

2.1.1 声发射信号的到时和定位

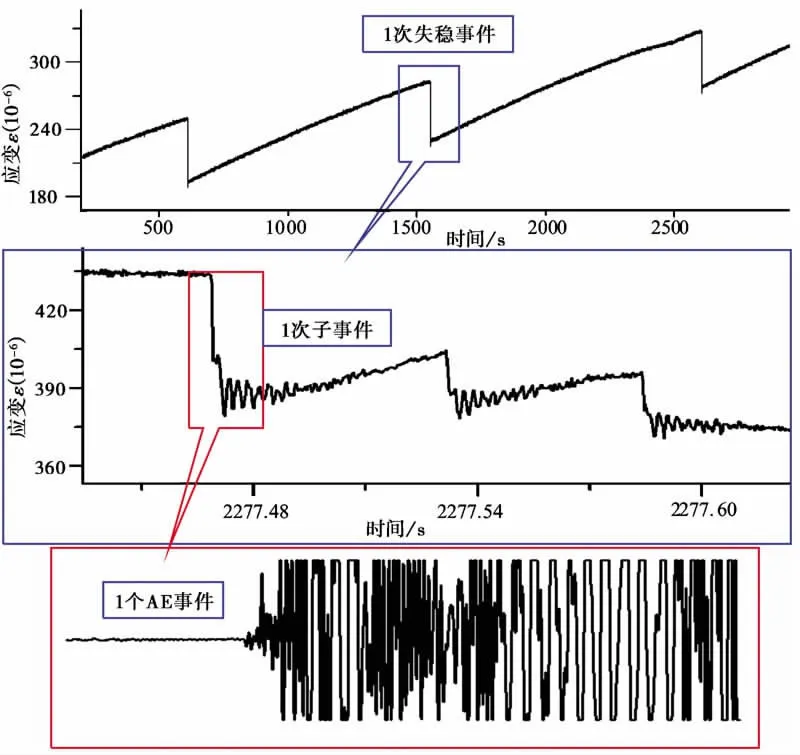
图4 失稳事件、子事件和AE事件关系图Fig.4 Relations between stick-slip event，sub-event and AE event.图中1次失稳粘滑事件中包含3个子事件，每一次子事件产生1个AE事件

将每一次错动子事件对应的各个通道波形到时进行分析，图5a，b，c中分别用短红竖线标出了每一个通道信号的初动到时。假定每一次子事件只有1个震源，并符合弹性波的传播关系。由最小初动到时的通道确定为该次子事件震源的大致位置，利用传播关系，根据相邻通道的距离与相邻通道接收声发射的到时差计算出其对应的传播速度。计算公式如下:

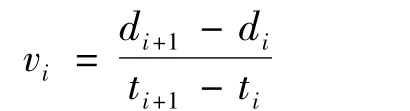
式中，di+1和di为相邻2个传感器的距离，ti+1和ti为相邻2个传感器接收声发射波的初动到时。计算结果如表1所示。从表1中的结果可以看到，每2个通道的速度相差很大，并不能获得一个相对一致的速度，甚至出现了负速度，即在同一个子事件里的各个通道的信号并非完全符合传播关系，从这个意义上说，在更次一级的一次子事件中也可能存在多个错动点源。

2.1.2 声发射的近场初动方位空间分布情况

在图5a中，No.5号AE事件中从12号探头到1号探头的初动方位均为负(图5 a);而No.6号事件中，1～4通道的初动方位较为清晰，均为正，而远离1通道的一些通道初动方位稍微比较不清晰(图5 b);图5c中，No.7号事件第2通道和第3通道的初动方位出现明显的反向现象，其第1，2通道的初动方位为负，而第3通道往后更大序号通道的初动方位为正(图5 c)。

表1 每次AE事件中两相邻通道的到时差所求得的速度(单位:m/s)Table 1 the velocity of adjacent channels of AE(m/s)

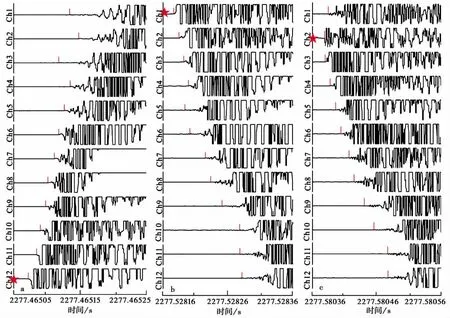
图5 第3次失稳粘滑事件中AE事件信号到时和波形初动空间分布图Fig.5 The distribution map of the arrival time and first motion of AE in No.3 stick-slip event.

经典的震源理论推测震源的周围地震波初动方位是呈四象限分布(Aki et al.，1980)。从某种意义上说，本次实验布置的1～12号传感器中，从平面上看，是半无限空间的辐射平面，相邻传感器接收到的AE波形初动方向的反向恰好指示了震源所在。因此，通过分析这3次子事件产生的声发射初动方位的空间分布，可以判断它们是来自不同震源。

2.2 应变场

本文讨论的应变是由1～12组应变花测量结果进行计算之后沿预制断层上的投影分量(本文以压应力为负值，张应力为正值)。

如图6所示。图6a，b为断层的一侧中12组应变花对应的正应变和剪应变。从总体上看，应变的空间分布不均匀(图6 a，b)。其中3 810s以前8次失稳事件中，每一次失稳事件均出现明显的3次应变值的快速改变(图4)。并且在应变值的快速变化之后的20ms期间内，应变出现频率较高的快速振动，其频率为300～600Hz不等。图6c为第3次失稳事件对应的正应变增量和剪应变增量沿断层的分布情况，从图中可以看出1次失稳粘滑对应的应变增量也极不均匀(图6 c)。

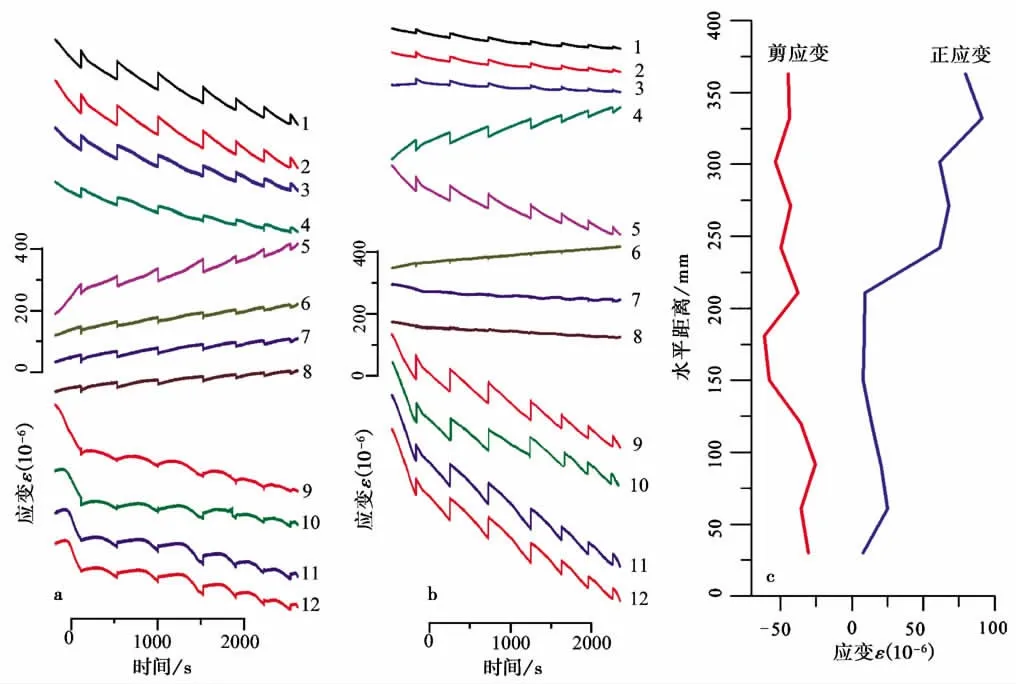
图6 应变时间、空间分布图Fig.6 The time-space distribution map of strain.

为了能与声发射相对比，笔者选取了第3次失稳事件中第11号应变花对应的瞬态应变场进行分析，如图7 b所示，从开始预滑到最后的粘滑停止，一共持续了620ms，整个失稳事件包含3次快速滑动阶段，这3次快速滑动震动共持续130ms，时间顺序上也有明显的差异，其中前2个事件的时间间隔为63.12ms(图7 b)，No.6与No.7号事件的时间间隔为52.19ms。这3次快速滑动的错动事件发生的时间间隔与对应的3个AE事件的时间间隔精确的一致。

单纯从应变资料来分析粘滑的多点错动，最新的研究发现:失稳事件包括预滑动阶段、快速滑动高频振荡阶段和低频波动止滑阶段3个完整的部分(图7 a)。包括本研究的最近一系列实验中，记录到有些粘滑事件并不是简单地分为以上这3个过程，在预滑动阶段之后，进入快速滑动震动，快速滑动之后并没有进入下一个低频波动止滑阶段，而是继续进入第2个快速滑动震动相阶段，之后进入第3个快速滑动震动相阶段。经过3次快速滑动震动之后，才进入低频波动止滑阶段(图7 b)。如果独立地将图中的①、②、③阶段对应的每一次快速滑动看作为1个子事件，而每一个子事件对应1个错动事件，因此从宏观上来看，1次粘滑失稳事件中包含不同时刻的3次错动子事件。

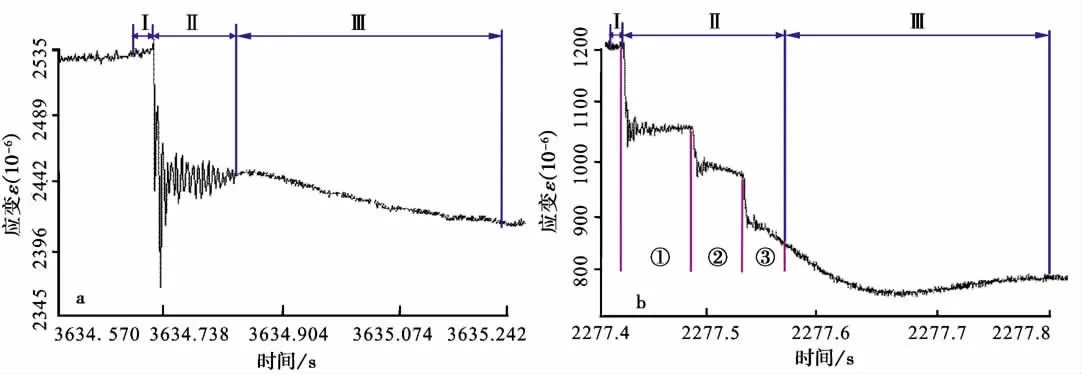
图7 失稳粘滑事件应变变化图Fig.7 The variation of strain of stick-slip event.

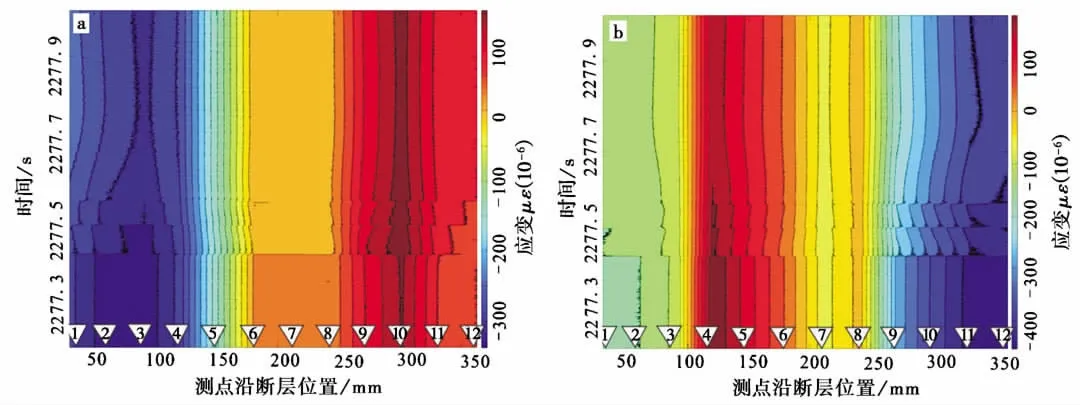
图8 第3次失稳粘滑瞬间应变分布图Fig.8 The distribution map of transient strain during the No.3 stick-slip event.

2.2.1 瞬态应变场分布情况

文中的瞬态应变场描述的是粘滑事件从预滑阶段到低频波动止滑阶段的应变场。从处理的应变场结果来看，沿断层的空间分布上正应变和剪应变都很不均匀，如图8 a所示:图中2号和3号应变花的正应变均比两旁的1号和4号小，出现局部的谷值。10号应变花中的正应变也比两旁的9号和11号应变花对应的正应变量大，也出现了局部的峰值(图8 a)。同样地，剪应变在4号8号以及11号应变花中也出现了多个峰值或谷值(图8 b)。这种在同一断层面上多个峰值或谷值的现象，很难用单震源来解释，而在多个震源的情况中，则会出现这种现象。

图9a和图9b是分别关于第3次失稳粘滑过程中正应变和剪应变增量分布图，从图中可以看到，正应变增量场和剪应变增量场都不均匀分布，而且关于某一点呈局部对称分布并出现局部极值现象(图9 a)，这表明在粘滑事件过程中，正应变或者剪应变是以局部对称中心为起始点，应变开始迅速改变，而这些起始点，可能是多点错动的震源所在。其对应的物理本质为应力场在空间上的不均匀分布。图9a，b中标出了声发射事件的定位，其位置与正应变和剪应变增量场出现的局部极大值的位置大致相符(图9 a，b)。

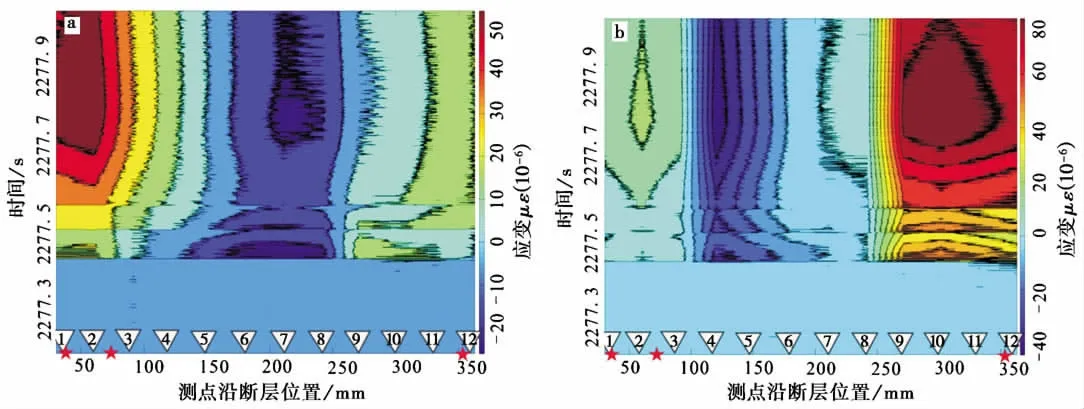
图9 第3次失稳粘滑瞬间正应变和剪应变增量场分布图Fig.9 The distribution of strain incremental field during the No.3 stick-slip event.

2.2.2 应变增量场空间分布情况

图9是第3次失稳事件在失稳前200ms到失稳后300ms期间沿着断层带的正应变增量场和剪应变增量场分布图。图9b中，第10、11和12号应变花对应的应变增量均为正值，第1和2号应变花对应的应变增量也为正值;第4、5和6号应变花对应的应变增量为负值(图9 b)。应变增量为正值时，对应的应变波表现为向外扩展;而对于负值，其对应的应变波表现为向内收缩，总体指示了在粘滑失稳瞬间应力沿断层的不均匀释放。剪应变增量场的初动空间分布，与上文对应的声发射波场的初动空间分布大致相对应，也能判定是非单点震源的初动空间分布模式。

3 讨论与结语

(1)高精度、高时间分辨率的观测证实，一次粘滑过程是由发生在断层上不同位置上的多次次级滑动组成的。高速应变系统清楚地记录到粘滑过程明确划分为2至3次子事件，每个子事件对应的最早的声发射波出现在断层的不同部位，表现出第1层次的多点滑动特征。沿断层带布设的声发射传感器可以记录到每个子事件发生瞬间各个位置接受到的振动信号。可以看到，各点的声发射信号起跳时间并不符合从最早的起点向外传播的规律，由此推测每个子事件的错动也是通过多点错动完成的。

(2)观测显示，沿着剪切面存在一个起伏变化的复杂应变场，高速瞬时滑动过程中沿断层带应变能的释放也是不均匀的。应变增量场中出现的局部极值点的位置与声发射事件的位置大体相符，AE初动方位和应变增量场的变化方向之间密切相关等特性都说明应变场的基本框架与能量释放特征构成了多点错动的基本力学条件。

(3)在以往的一些研究中，常常将一些大粘滑事件对应的声发射事件无法定位归结于信号的噪声太大，到时的拾取误差和算法以及系统的时间不同步等(马瑾，1995;马文涛，1995a，b;雷兴林，1995;刘力强，1999;蒋海昆等，1999;巴晶等，2004;胡新亮等，2004;刘培洵等，2009)。从多点滑动的观点上看，难以定位的原因还可能是由于同一组到时波形未必来自一个震源，建立在单点源模型上的各种数据计算处理方法自然无法求得正确结果。从这个意义上看，以往的粘滑事件无法定位现象，说明了多点错动现象早已经被观测过，只是没有被发现。

(4)本实验记录到了震源的多点错动现象，它们大多可以在应力降(起始破裂尺度)较大的失稳事件中被观测到，小能量事件对应的起始破裂的尺度较小，记录尚不清楚。这与天然地震中报告的多点震源现象多见于大地震而小地震由于破裂尺度与波长的关系难以被记录的情况是一致的。所以一般来说，应当认为地震粘滑过程本质上是非均匀的，必然存在不同尺度的多点滑动现象。在一定灵敏度的观测系统中，可能观测到一定能量范围的大事件多点滑动事件，小事件则由于分辨率不足，被当作了均匀过程。在极近场条件下，往往容易获得多点错动，而远场情况下各次微小错动之间的差别可能被淹没。尺度的大小是同时相对于事件强度与观测距离而言的。在实践中，需要根据实际情况，判断选择合理的震源物理模型。