基于反步法的单管正激变换器控制

王鹏云

(宝鸡文理学院，陕西 宝鸡 721016)

0 引言

反步法(Backstepping)是Kokotovic教授提出的一种控制系统方法。它的设计思想是:针对满足严格反馈控制结构的系统，通过反向递推设计，用系统化的方法同时构造Lyapunov函数和镇定控制器。基于反步法的控制器设计方法，其基本思路是将复杂的系统分解成不超过系统阶数的子系统，然后通过反向递推设计为每个子系统设计部分Lyapunov函数和中间虚拟控制量，直至完成整个控制器的设计。反步设计方法既适用于线性系统也适用于非线性系统，对带有参数严格反馈形式的非线性系统尤为有效。因此它在非线性控制领域得到了广泛应用[1][2]57[3－4]。

被广泛应用的单管正激变换器是一类典型的开关非线性系统[5]，为了提高其静态性能和动态性能，本文将 Backstepping应用于变换器系统中。首先根据其工作原理建立了参数严格反馈形式的二阶非线性系统数学模型，对建立的非线性系统模型，采用反步法设计全局渐进稳定的控制器，使每个状态分量具有适当的渐进特性，从而实现整个系统在大扰动下的全局渐进稳定性。依据得到的反馈控制律组建闭环控制系统，验证了此控制方案的正确性。

1 单管正激变换器的数学模型分析

一般的单管正激变换器电路拓扑如图1所示。变压器绕组W3和二极管VD3组成磁复位电路。开关管VS及驱动信号如图2所示，其中Ts为开关周期，d为VS在一个开关周期内占空比，uGEM为驱动电压额定值。横轴是时间轴，单位是毫秒，纵轴为驱动电压信号，单位为伏特。

设电路工作在输出电感电流连续模式下，根据其工作原理，在0＜t≤dTs时，开关管导通。令n=N2/N1，根据基尔霍夫定律得到(1)式:

在dTs＜t≤Ts时，开关管关断。同理有:

由于一个开关周期存在两个方程，现定义一个开关函数S将式(1)、(2)统一为式(3)，其中 S=1，表示 VS 导通，S=0，表示 VS关断。

方程中出现开关函数，系统是离散的，引入开关周期平均算子式(4)将其变换为连续的系统，x(t)为电路中的某电量[6]。

对开关函数求开关周期平均后得到式(5)

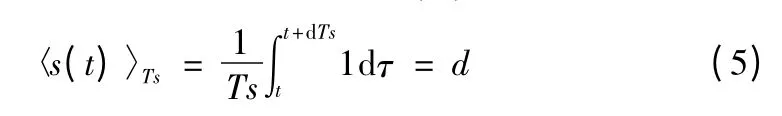
对统一方程求开关周期平均后，得到:

以上各量虽为开关周期平均值，仍保持原有书写格式。式中d为控制输入量，u0为系统输出。从系统的数学模型可以看出，式(6)为具有参数严格反馈形式的非线性系统。它隶属于式(7)统一表达式[2]。

2 单管正激变换器的反步设计方法

单管正激变换器数学模型属于严格反馈控制结构的系统，可以应用反步设计方法。因系统的阶数为2，整个设计可分为两步。

单管正激变换器控制目标是其输出跟踪给定。

(1)定义跟踪误差

式中uoref为给定值。对上式求导得到:

定义 β(u·oref，uo)函数和辅助误差e2函数:

其中iLref为虚拟控制量。

将上两式代入式(9)中可得:

根据误差系统，设计虚拟控制量iLref为:

式中k1∈R+为反馈增益。将式(13)代入式(12)得到:

从上式可知:若 e2→0，则 e1→0。

选取Lyapunov函数为:

对上式求导，将式(14)带入得到:

(2)设计控制量d

对式(11)求导得到:

设计控制量d为:

式中k2∈R+为反馈增益，将上式代入式(17)得到:

选取Lyapunov函数为:

对上式求导，将式(16)、(19)带入得到:

由上式可知，Lyapunov函数的导数为负定的，系统渐进稳定。

从上述讨论知，得到反馈控制量d可按下式得到:

3 实验研究

3.1 实验参数

实验参数如下:直流电压uin=300 V，n=0.3，给定输出电压为30 V，开关周期为 Ts=0.04 ms，负载电阻 R0=5 Ω，输出滤波电感Lf=3 mH，电容Cf=150 μF。其中电压传感器采用 CHV－25/400霍尔传感器，电流传感器采用CHB－25NP霍尔传感器，实验采用TMS320F2812 DSP为控制器，功率器件选为IRFP460 414KAX。反馈增益为k1=1 000，k2=2 000。

3.2 实验结果

3.2.1 系统启动波形

图3为输出电压u0、电感电流iL的启动波形，从波形上看启动速度快，过渡时间为8 ms左右，输出电压基本无超调，输出电压无静差。

3.2.2 负载变化实验波形

负载由R0=5 Ω突变为R0=2.5 Ω，实验波形如图4，从实验波形可以看出，系统在负载突变后4 ms左右系统稳定，输出电压完全跟随给定且无静差，说明系统抗负载扰动能力强。

3.2.3 电源电压变化实验波形

uin变化为300 V→240 V→300 V和300 V→370 V→300 V，实验波形为图5。从实验波形可以看出:直流电压变化时，输出电压和电感电流基本恒定，说明对直流电压变化扰动抵抗能力很强。从公式(18)知，控制占空比对直流电压波动有前馈作用。

4 结束语

本文建立了单管正激变换器的具有参数严格反馈形式的二阶非线性系统数学模型。提出对此模型应用反步设计法，推导出反馈控制律的一般表达式。并应用此反馈控制规律组建单管正激变换器闭环控制系统。实验结果表明，系统具有良好的静态性能和动态性能，验证了该控制策略的正确性和可行性。

图5 电源电压突变时实验波形

[1]胡跃明.非线性控制系统理论与应用[M].北京:国防工业出版社，2005:188－193.

[2]王莉，王庆林.Backstepping设计方法及应用[J].自动化博览，2004，22(6):57－61.

[3]Yang J H.Wu J，Hu Y M.Backstepping method and its applications to nonlinear robust control[J].Control and Decision.2002，17(S):64l－647.

[4]朱晓荣，李和明，彭咏龙，等.基于反步法的电流型PWM整流器控制策略[J].电工技术学报，2007，22(2):78 －83.

[5]潘尚智，钱照明，雷娜.一种新型的通用单/双正激型直流变换器电路仿真平均模型[J].中国电机工程学报，2001，21(06):58－62.

[6]徐德鸿.电力电子系统建模与控制[M].北京:机械工业出版社，2006:6－12.