二维玻色-爱因斯坦凝聚中孤立波的调制不稳定性*

张恒 段文山

(西北师范大学物理与电子工程学院,兰州 730070)

(2012年8月27日收到;2012年9月4日收到修改稿)

1 引言

自从1995年玻色-爱因斯坦凝聚在碱金属原子中实现以来,人们在实验和理论方面对它做了大量的研究[1−13].这些研究工作又一次燃起了人们对这一物态的研究兴趣[14,15],其中一个令人极其感兴趣的问题是玻色-爱因斯坦凝聚(BEC)的动力学行为[16−18]研究.在零温极限情况下,所有原子都发生凝聚,这使得体系很自然地可以用平均场下的Gross-Pitaevskii(GP)[19]方程来描述.并且在该理论下还发现了BEC系统所满足的Korteweg-de Vries(KdV)方程和暗孤子[20−24].众所周知,在很多物理研究领域内都发现了孤子,比如尘埃等离子体[25,26]、激光等离子体[27]、BEC系统[28−31]、二维系统[32]等.

自从在BEC系统中发现孤子以来,调制不稳定性是孤子研究[33]中的一个有趣的问题.可以确定的是对于单组分BEC系统的稳定性可用标记原子之间相互作用的方法来惟一确定.由于原子的相互作用[34,35],在原子数目的最大临界值以内凝聚是稳定的.因为有外部原子源的存在,当原子数目超过最大临界值时,由于BEC内的原子相互作用半径趋于零导致中心凝聚密度区域无穷大.因此,凝聚开始塌缩发射出原子,直到原子数目减少到临界值以下结构达到稳定.然后凝聚物又开始堆积,一系列的塌缩也伴随发生.

继文献[33]的研究工作之后,我们给出一种处理GP方程以及从二维非线性Schrodinger方程(NLSE)出发去描述BEC中孤立波的方法,并得出了色散关系的显示式,同时,还解析研究了单组分常振幅BEC(TBEC)的调制不稳定性.

2 二维非线性Schrodinger方程的导出

假设用波函数来描述粒子数为N具有相同量子态的凝聚气体.在低温情况下,具有弱相互作用的玻色气体的动力学行为可以用含时的Gross-Pitaevskii方程来描述,写出序参量[36]

这里的U0=4π¯h2as/m是相互作用常数,as是原子间s波散射长度(具有排斥相互作用的系统as＞0),m为原子质量.假设粒子被限制在具有盘状势Vext=m[ω(x2+y2)+ωz2]/2的阱中,ω⊥代表x轴或y轴的横向频率,ωz为z方向的势阱频率.为了方便变量无量纲化,规定x=[/(mωz)]1/2ξ,y=[/(mωz)]1/2η,z=[/(mωz)]1/2ζ,t=(ωz)−1τ.

将这些变量带入方程(1)中则有

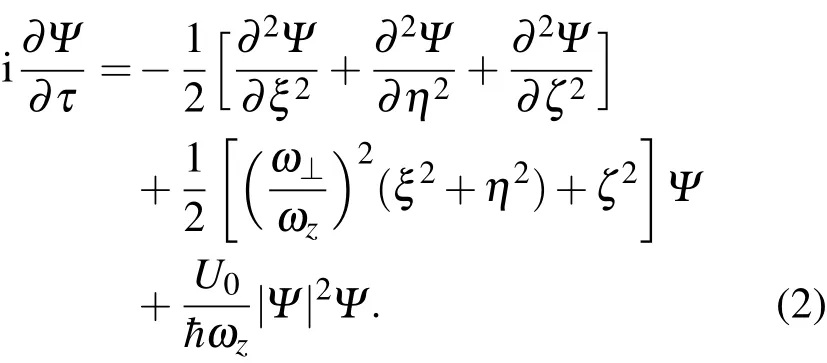
由于盘状势ω⊥/ωz非常小,因此 (ω⊥/ωz)2可以被忽略.然后有:

假设势阱的x轴和y轴是相互垂直的,可以把波函数写成Ψ=f(ξ,η,τ)g(ζ),g(ζ)满足

方程(4)就是大家熟知的一维量子谐振子本征方程,它的基态解的形式为g0=exp(−ζ2/2),对应的本征值为ν=1/2.将波函数的表达式代入方程(3),并乘以g∗可以得到

将方程(4)代入方程(5),得到如下形式:

通过如下的变换

可以得到

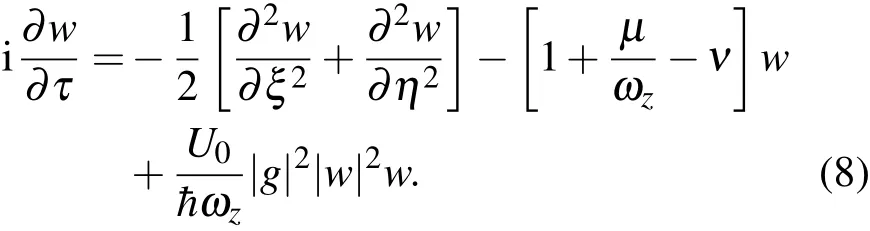
给方程(8)左右同乘 e−ζ2/2,让方程(4)中g=g0并代入方程(8)中,对ζ积分一次以消除方程对ζ的依赖,得到

其中

这里的µ是化学势.

3 TBEC的调制不稳定性

这一部分将研究TBEC的调制不稳定性.将方程(9)中的振幅w分成如下的两部分:

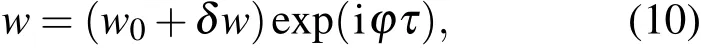
其中w0是孤立波的常实振幅,δw(δw≪w0)是小振幅微扰,φ是非线性频移.把方程(10)代入方程(9)中并保留零阶项和一阶项(线性化),得到

这里的δw∗是δw的复共轭.把δw=X+i Y代入方程(12)中,并将实部和虚部分开,得到如下耦合方程:

假设振幅微扰δw=X+i Y,其中

这里的Ω是调制波的频率.Kξ和Kη分别为ξ和η方向的调制波数.用方程(15)和(16)可以得到非线性色散关系

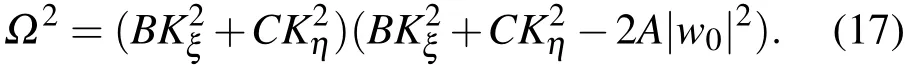
由方程(17)可以推断,如果满足如下条件:1)B＞0,C＞0且A＜0;2)B＜0,C＜0且A＞0,Ω2＞0.对于以上条件,Ω是实数,所以孤立波是稳定的.上文中考虑的条件对于as＞0所对应的原子间相互作用力为斥力,因此TBEC的孤立波是稳定的.相反,如果Ω2＜0,Ω是虚数,那么TBEC的孤立波是不稳定的.这样看来是存在调制不稳定的条件.

为简单起见,令Kη=0,那么微扰振幅只在ξ方向上.鉴于这种情况,方程(17)的色散关系可以被重新写作Ω2=B2KK−2(A/B)|w0|2].因此,满足条件1)BA＜0,2)BA＞0但K2(A/B)|w0|2时,TBEC中的孤立波是调制不稳定的.这样看来,孤立波的稳定性依赖于A/B的符号.当波数Kξ满足K＜2(A/B)|w0|2,如果B和A同号,TBEC中的孤立波是调制不稳定的.当原子间相互作用了为引力,as＜0,AB＞0时,如果K＜2(A/B)|w0|2,孤立波是不稳定的,然而如果K＞2(A/B)|w0|2,孤立波是稳定的.因此,对于原子间相互作用力为斥力,as＞0,AB＜0时,对于所有条件孤立波都是调制稳定的.

由条件dΩ/d Kξ=0,可以找到增长率的最大值.当时,与增长率最大值相应的频率可由γmax=|A||w0|2得到.如果Kξ=0,微扰振幅只在η方向存在.那么方程(17)的色散关系可以重新写作Ω2=C2K[K−2(A/C)|w0|2].对于以上条件可以类似地做稳定性分析.

4 结论

本文由GP方程出发,推导出了二维Schr¨odinger方程.研究了TBEC中孤立波的调制不稳定性.研究发现,as＞0对于任何条件孤立波都是调制稳定的.而对于条件as＜0,孤立波在K2＞2(A/B)|w0|2和K2＜2(A/B)|w0|2情况下分别为稳定和不稳定.同时,如果扰动的波数足够大,那么波是稳定的,否则是不稳定的.

[1]Wen W,Shen S Q,Huang G X 2010 Phys.Rev.B 81 014528

[2]Zang X F,Li JP,Tan L 2007 Acta Phys.Sin.56 4348(in Chinese)[臧小飞,李菊萍,谭磊2007物理学报56 4348]

[3]Wang G F,Fu L B,Liu J 2006 Phys.Rev.A 73 13619

[4]Li S C,Fu L B,Duan WS,Liu J 2008 Phys.Rev.A 78 063621

[5]Wen W,Huang G X 2009 Phys.Rev.A 79 023605

[6]Ma Y,Fu L B,Yang Z A,Liu J 2006 Acta Phys.Sin.55 5623(in Chinese)[马云,傅立斌,杨志安,刘杰2006物理学报55 5623]

[7]Madison K,Chevy F,Bretin V,Dalibard J 2000 Phys.Rev.Lett.84 806

[8]Svidzinsky A A,Fetter A L 2000 Phys.Rev.Lett.84 5919

[9]Jochin S,Bartenstein M,Altmeyer A,Hendl G,Hecker Denschlag J,Grimm R 2004 Phys.Rev.Lett.91 240402

[10]Wang G F,Fu L B,Liu J 2006 Phys.Rev.A 73 13619

[11]Liu J,Wu B,Niu Q 2003 Phys.Rev.Lett.90 170404

[12]Wu Y,Yang X X 2003 Phys.Rev.A 68 013608

[13]Hu B B,Huang G X,Ma Y L 2004 Phys.Rev.A 69 063608

[14]Legget A J 2003 Rev.Mod.Phys.75 1083

[15]Trombettoni A,Smerzi A 2001 Phys.Rev.Lett.86 2353

[16]Gerton J M,Strekalov D,Prodan I,Hulet R G 2001 Nature 408 692

[17]Men F D,Liu H,Fan Z L,Zhu H Y 2009 Chin.Phys.B 18 2649

[18]Liu J,Fu L B,Ou B Y,Chen S G,Chin D,Wu B,Niu Q 2002 Phys.Rev.A 66 023404

[19]Bradley C C,Sackett C A,Hulet R G 1997 Phys.Rev.Lett.78 985

[20]Huang G X 2001 Chin.Phys.Lett.18 628

[21]Yang X X,Shi Y R,Duan WS 2008 Commun.Theor.Phys.49 119

[22]Hang G X,Zhu S H 2002 Chin.Phys.Lett.19 17

[23]Duan WS,Chen JH,Yang H J,Shi Y R,Wang H Y 2006 Chin.Phys.Lett.23 2000

[24]Song S W,Wang D S,Wang H Q,Liu W M 2012 Phys.Rev.A 85 063617

[25]Liang GZ,Han JN,Lin M M,Wei JN,Duan WS 2009 Phys.Plasmas 16 073705

[26]Jiang X,Gao X Y,Li S C,Shi Y R,Duan W S 2009 Appl.Math.Comp.214 60

[27]Tian D X,He G J,Han J N,Duan W S 2009 Commun.Theor.Phys.51 529

[28]Li S C,Han J N,Duan WS 2009 Physica B 404 1235

[29]Li S C,Duan WS 2008 Commun.Theor.Phys.50 655

[30]Li B,Zhang X F,Li Y Q,Chen Y,Liu W M 2008 Phys.Rev.A 78 023608

[31]Hu X H,Zhang X F,Zhao D,Luo H G,Liu W M 2009 Phys.Rev.A 79 023619

[32]Han J N,Du S L,Duan WS 2008 Phys.Plasmas 15 112104

[33]Duan WS,Parkes J,Zhang L 2004 Phys.Plasmas 11 3762

[34]Gammal A,Frederico T,Tomio L,Chomaz P 2000 Phys.Rev.A 61 051602

[35]Kagan Y,Muryshev A E,Shlyapnikov G V 1998 Phys.Rev.Lett.81 933

[36]Dalfovo F,Giorgini S,Pitaevskii L,Stringari S 1999 Rev.Mod.Phys.71 463

[37]Duan WS,Parkes J,Lin M M 2005 Phys.Plasmas 12 022106