梁结构损伤诊断直接指标法应用
2013-12-12包振明赵德有林哲马骏
包振明,赵德有 ,林哲,马骏
(大连理工大学 船舶工程学院,大连 116023)
0 引言
在目前所涉及的损伤指标中,基于应变模态的损伤指标灵敏度较高。但应变类损伤指标大多数只能定位损伤,同时需要损伤前后的模态数据。在工程实际中,突发事件及地质灾害等情况下,损伤前的精确状态难以获得,因而难以运用。顾培英[1,2]提出了无健康标准下基于应变模态差分(Strain Mode Shape Difference)原理的ISMSD直接定位损伤指标法,解决了此问题。该指标综合考虑了相邻量两有效极值点间有效距离比、有效极值之差绝对值、有效极值绝对最大值等三个元素,适用于未安装健康监测系统的结构损伤诊断。本文应用该指标法计算了非贯穿损伤梁损伤位置直接指标,判定出损伤位置。.
1 应变模态分析的理论基础
连续弹性体结构的试验模态分析是利用一系列离散测点的位移值来描述其各阶振型函数,求取的各阶模态是这些离散点归一化的位移值之比。应变分布可由变形位移经微分运算求得。
直欧拉梁横向自由振动的微分方程为:
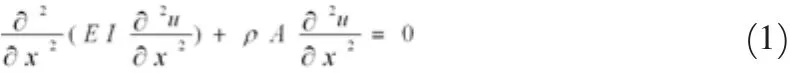
梁各阶位移模态Ør(x) (r=1,2,…)表示为:

通过对位移模态的差分运算求取曲率模态,结构的离散曲率模态振型可以通过中心差分格式[3]近似求出:

其中Ørk为第r阶位移振型幅值;k为计算点;h为相邻计算点的距离。设z(x)是弯曲变形中面到某一点的距离,则该点在x方向的应变[4]为:

应变模态和曲率模态的关系可由此导出。应变模态振型比位移型指标对损伤具有更好的识别能力。
2 损伤梁应变模态差分模型
本文主要针对简支梁结构这种常见的结构形式,尤其是应变模态曲线在损伤处存在极值并发生突变,求导需经三次样条插值光滑处理。中心差分法是求导最常用的数值方法之一,其对称性、一定的精度、使用方便是该方法的优点,在非边界结点采用中心差分格式,边界结点采用偏心差分格式。
若将一维梁式结构划分成等间距为h的n-1个单元,即n个结点。 为r阶应变模态函数,等间距基本差分格式:

边界结点1的差分公式:

边界结点n的差分格式:

差分曲线拟合时,需要应用两端点处差阶差分值,可导出:

损伤应变模态曲线的极值点位于损伤突变区及模态振型峰值处。存在曲线突变的位置就是结构损伤处。对于实际工程,由于试验测点布置或仿真计算单元划分未必正好处于损伤处、试验或计算精度问题及差分计算精度问题,理想的曲线极值点导数未必正好为零。
为解决应变模态差分曲线的问题,本文采用插值法。结点处计算值与假定函数相等。需计算多个插值点的函数值,并绘出函数曲线。采用应用最为广泛的三次样条函数插值来平滑数据。
3 算例
一含局部边缘损伤简支梁(图1),几何尺寸长400mm ,宽10mm,高2mm,损伤位置在四分之一跨处,损伤长度为梁宽度的1/5。取弹性模量211GPa、密度7850kg/m3、泊松比0.33。损伤量为有效截面高度的6.25%,12.5%,25%,31.25%。应用ANSYS有限元分析软件的8结点solid45实体单元建模,网格划分为横向25等分,竖向16等份,损伤宽度为2mm。根据应变模态数值仿真[5,6]结果,应用中心差分格式及三次样条插值算法,求出光滑应变模态差分曲线。

图1 局部损伤简支梁有限元模型图
4 损伤应变模态差分曲线
图2~图5是经过三次样条插值后的损伤量为有效截面高度的6.25%、12.5%、25%、31.25%的应变模态差分曲线。

图2 损伤6.25% 前三阶应变模态差分曲线

图3 损伤12.5% 前三阶应变模态差分曲线

图4 损伤25% 前三阶应变模态差分曲线

图5 损伤31.25% 前三阶应变模态差分曲线
除支座外,应变模态差分曲线只在损伤处发生剧烈变化,损伤量不同,差分曲线突变程度略有不同。随损伤量的增大,损伤处曲线突变增大,其规律相似。
5 直接定位损伤指标数学模型
5.1 损伤位置直接定位指标
损伤指标由突变区极值点间数据变化规律提出,曲线的变化程度可由其导数体现。
5.1.1 有效距离比
相邻两有效极值间的距离定义为有效距离,有效距离与跨度之比定义为有效距离比。假定跨度为l,有效极值点x0,x1,x2,…, xp对应的有效极值为y0,y1,y2,…, yp有效距离比定义为:


表1 损伤位置定位指标
相邻两有效距离比越小,其间发生损伤可能性越大。

5.1.2 有效极值的绝对最大值ISMSD
由于不同阶之间模态差分曲线非归一化,因而将式(11)计算结果除以各阶有效极值最大值,即可消除不同阶的影响。
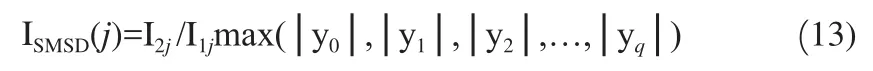
即:

式(14)即为损伤位置直接定位指标。数值越大,损伤可能性越大。再结合差分曲线变化规律,基本能确定损伤位置。
根据图1,图2,图3,损伤位置判定计算结果如表1所示。
6 结论
对于梁早期损伤,并未出现宏观裂缝,损伤处应变模态差分曲线会发生突变,数值可能不为零。由表1可知:前两阶损伤处指标明显最大,并随损伤量增大而增大。该指标能判定损伤位置,尤其是损伤量较小的时候。
[1]顾培英, 邓昌, 吴福生.结构模态分析及其损伤诊断[M].南京: 东南大学出版社, 2008.
[2]顾培英, 陈厚群, 李同春, 邓昌.基予应变模态差分原理的直接定位损伤指标法[J].振动与冲击, 2006(25):13-17.
[3]张汝清, 殷学刚, 董明.计算结构力学[M].重庆: 重庆大学出版社, 1987.
[4]李德葆, 陆秋海, 秦权.承弯结构的曲率模态分析[J].清华大学学报(自然科学版), 2002 (2):224-227.
[5]金咸定, 赵德有.船体振动学[M].上海: 上海交通大学出版社, 2000.
[6]徐芝纶.弹性力学[M].北京: 高等教育出版社, 1985.
