基于球谐函数模型的GPS差分码延迟估计

张 伟，邱卫宁，畅 鑫

(1.武汉大学测绘学院，湖北武汉430079;2.武汉大学灾害监测与防治研究中心，湖北武汉430079)

一、引 言

GPS码间偏差(difference code bias，DCB)是指由于硬件延迟造成的同一时刻不同频率或同一频率上不同伪码观测量之间的时间偏差，它包含卫星码间偏差及接收机码间偏差。由于接收机的DCB与接收机硬件有关，借助对实测数据计算DCB值的时间序列分析可监测GPS接收机硬件的性能。我国学者袁运斌等对GNSS DCB的处理进行了系统的研究［1-4］。卫星的 DCB通常被认为是一个长期的稳性值，但IGS分析中心通过对长期的观测数据分析发现卫星的DCB存在跳变现象，目前跳变值的预报依旧是一个难题。

在利用GPS测量时，一些情况下(如使用单频接收机C1/X型和C1/P2型接收机)必须考虑硬件延迟的影响［5-6］。同时，在利用观测数据对电离层TEC进行估计时，忽略卫星DCB的影响会导致3～10 ns的误差(0.1 ns约引起3 cm的距离误差)。因此，求取不同测距码的DCB值不论是对定位还是对建立电离层模型都是非常重要的。本文利用IGS跟踪站同时含有P1、P2、C1码观测值的接收机的观测数据，通过建立去几何相关性的观测方程［7］对以上3种测距码间卫星DCB进行了实时解算，并与IGS发布值进行了对比。

二、DCB解算模型

1.GPS伪距观测原理

GPS测量中，由于卫星钟、接收机钟的误差，以及电离层和对流层中的延迟，实际测出的距离与卫星到接收机的实际几何距离有一定的差值，因此一般称测距码测得的观测值为伪距。

目前，GPS测量中常见的伪距观测值主要有P1、P2、C1，其伪距观测方程如下

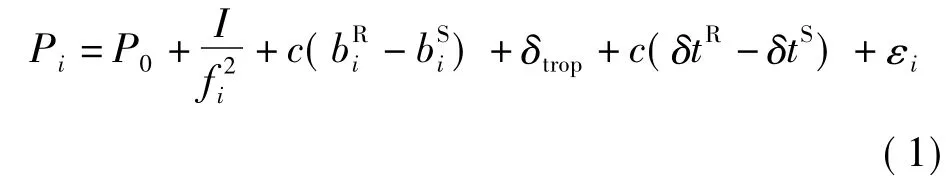
式中，Pi为第i频点实测伪距;P0为对应理论星地距;I为观测历元电离层改正因子;fi为接收机频率;c为光速;分别为第i频点卫星及接收机硬件延迟误差;δtR、δtS为测站及卫星钟差;δtrop为对流层延迟;εi为伪距观测误差，包含多路径效应。改正值体现在卫星钟差上，其测量基准为卫星钟时标。目前，由于IGS发布的GPS精密星历中的卫星钟差是利用双频无电离层组合观测量计算得到，其采用的测距码观测值为P1、P2，因此组合使用这些星历及单频观测数据时必须仔细对伪距观测量进行、改正［8］。

2.DCB解算模型

在GPS观测之中，除了伪距观测值外，还有载波观测值，由于伪距观测值的观测噪声远大于载波观测值的观测噪声，因此可以采用载波相位观测值平滑差分伪距，从而减小观测噪声的影响。载波观测方程如下

式中，L为GPS载波相位观测值;ρ为接收机与卫星真实几何距离;dion为电离层延迟量;dtrop为对流层延迟量;c为光速;τi为卫星钟差;τj为接收机钟差;d为卫星、接收机码硬件延迟;b为卫星、接收机载波相位硬件延迟;N为载波相位模糊度;ε为GPS观测值噪声;k=1，2，为L1、L2 频率;i为卫星;j为接收机。

伪距(以C1、P2码为例)和载波差分观测方程如下

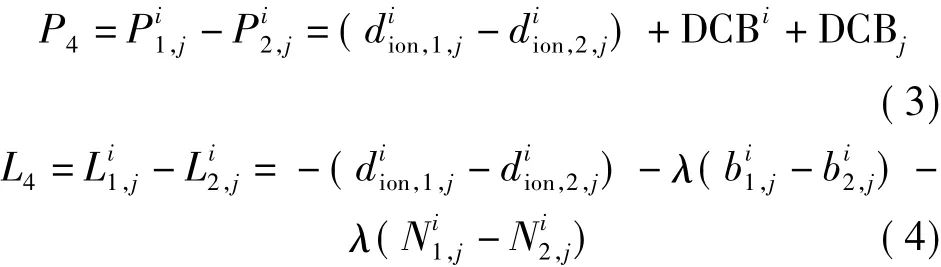
式中，DCBi、DCBj分别为卫星和接收机差分码延迟。由于伪距精度较低，故采用L4平滑P4，在平滑之前应使用MW(Melbourne-Wübbena combination)和电离层残差法对L1和L2进行周跳探测，在数据处理时去掉存在周跳的观测数据。

利用双频载波差分值对伪距差分观测值进行平滑时，如果测距码为同一载波搭载，则会消去电离层差分项。为了在估计DCB的同时对电离层模型进行估计，按式(3)分别计算P1、P2和C1、P2的差分观测值并建立观测方程。由于载波噪声小，故采用L4平滑P4，下面给出平滑方程［9］

电离层对GPS伪距观测值所造成的影响可以表示为(忽略二、三阶项的影响)

式中，f为载波频率;STEC为倾斜路径总电子含量。将式(7)代入式(3)，并进行相位平滑伪距得到

天顶方向总电子含量VTEC与STEC的关系为

针对不同大小的区域网可以将VTEC表达为穿刺点经度、纬度的不同阶数的球谐函数模型，IGS全球电离层模型采用15阶，鉴于本文采用区域IGS站解算，故采用4阶［10］即可。由于上述模型只适用于P1、P2和C1、P2的码偏差的解算，因此对于C1、P1的码偏差可利用P1、P2和C1、P2的码偏差结果求差得到。但是，根据式(3)无法分离接收机和卫星的DCB值，为了求取卫星绝对DCB值，还需引入一个基准条件。本文采用IGS的基准条件是所有GPS卫星DCB值的和为0，即

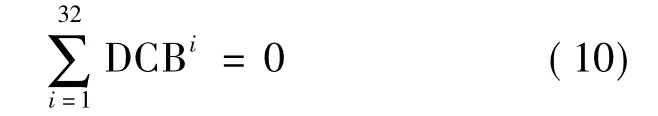
至此，常用测距码 C1、P1、P2的 DCB计算完毕。

三、DCB解算结果分析

本文采用IGS发布的2010年第3天的数据观测数据进行解算，并将P1、P2和C1、P1计算得到的DCB与IGS网站发布的进行对比。文中计算了两组数据，其区域大小基本一致，第1组采用IGS跟踪站分别为HRM1、BRUS、OPMT、REDU、WSRT、PTBB，经度最大相差12°，纬度最大相差4°;第2组分别为GOPE、GRAS、ONSA、POTS、PTBB、SOFI，经度最大相差16°，纬度最大相差15°。图1、图2分别给出了两组数据P1、P2和C1、P1码偏差与IGS发布值的差异信息;图3给出了两组数据计算得到的C1、P2码偏差差异信息。

图1 P1、C1 DCB对比图

图2 P1、P2 DCB对比图

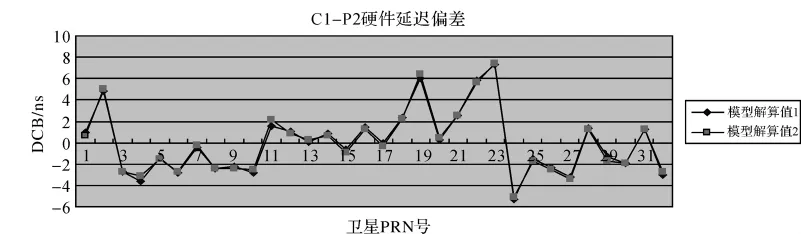
图3 C1、P2 DCB对比图

从图1、图2中可以看出，利用模型计算得到的DCB值与IGS发布的DCB值十分吻合，尤其是P1、P2码的DCB值。由于IGS没有发布C1、P2码偏差值，故无法进行比较。从图中可以看出，不同频率间硬件延迟一般比同频率间大，最大可以接近8 ns(约2 dm)，这会给利用组合方程定位或者建立电离层模型带来较大误差。

四、结束语

目前，GPS已经不再局限于传统的定位测量，而是在与其他学科进行相互交叉融合。尤其在气象学方面，利用GPS对电离层进行研究时，DCB的解算已成为一个不可忽视的问题，而且在动态精密单点定位中也必须考虑组合观测值的DCB的影响。因此，本文利用载波平滑后的差分伪距建立观测方程，对局域网的不同测距码的DCB进行了解算，并且与IGS发布值进行了比较，其结果与IGS发布值十分吻合，从而说明利用此模型可以得到P1、C1、P2相互间的所有DCB值，且结果较好。

［1］袁运斌，欧吉坤.GPS观测数据中的仪器偏差对确定电离层延迟的影响及处理方法［J］.测绘学报，1999，28(2)：110-114.

［2］YUAN Yunbin，OU Jikun.An Improvement to Ionospheric Delay Correction for Single-frequency GPS User—the APR-I Scheme［J］.Journal of Geodesy，2001，75(5-6)：331-336.

［3］袁运斌，欧吉坤.建立GPS格网电离层模型的站际分区法［J］.科学通报，2002，47(8)：636-639.

［4］袁运斌，霍星亮，欧吉坤.精确求定GPS信号的电离层延迟的模型与方法研究［J］.自然科学进展，2006，16(1)：40-48.

［5］LE A Q，TIBERIUS C.Single-frequency Precise Point Positioning with Optimal Filtering［J］.GPS Solutions，2007，11(1)：61-69.

［6］张小红，李星星，郭斐，等.GPS单频精密单点定位软件实现与精度分析［J］.武汉大学学报：信息科学版，2008，33(8)：783-787.

［7］CHANG K H，D A GREHNER-BRZEZINSKA，KOWN J H.Efficient GPSReceiver DCB Estimation for Ionosphere Modeling Using Satellite-Receiver Geometry Changes［J］.Earth Planets Space，2008(60)：25-28.

［8］宋小勇，杨志强，焦文海，等.GPS接收机码间偏差(DCB)的确定［J］.大地测量与地球动力学，2009，29(1)：127-131.

［9］李征航，黄劲松.GPS测量与数据处理［M］.武汉：武汉大学出版社，2005.

［10］JINR，JINShuanggen，FENGGuiping.M_DCB：Matlab Code for Estimating GNSS Satellite and Receiver Differential Code Biases［J］.GPS Solutions，2012，16(4)：541-548.