一种能见度测量修正方法及其应用研究

2013-12-10邢向楠崔岩梅李涛冷杰

计测技术 2013年3期

邢向楠，崔岩梅，李涛，冷杰

(中航工业北京长城计量测试技术研究所，北京100095)

0 引言

作为计算能见度的经典公式，Koschmieder 公式在其推证中作了一些假设［1］，严格按照该公式算出的能见度往往与实际情况不符。事实上，能见度测量仪器常采用的能见度计算公式都不是原始的Koschmieder 公式，而是以它为基础的实验验证公式或称经验公式。采用经验公式计算能见度能够减少测量仪器的算法误差，使得仪器测量结果最大限度地与能见度实际状况吻合。然而，国外能见度测量的修正方法及其经验公式在文献资料中很少披露，国内相关研究也无从借鉴。

其实，这些验证公式可以采用下述方法得出:首先在Koschmieder 公式中加入修正系数，建立能见度精确计算的普遍形式的数学模型;其次通过实验获得真实能见度与仪器输出信号的对应数据，代入普遍数学模型求出修正系数具体值;再者将修正系数具体值回代到普遍数学模型;最后得出能见度精确计算的工作公式［2］。本文所讨论的能见度经验公式引入二系数修正模型并推至更具普遍意义的多项式拟合，应用于能见度测量装置的修正，通过装置与参考仪器的比对实验，研究数学模型的合理性。

1 修正公式的引入

普遍形式的修正数学模型中，实用价值较大的有二系数修正方程和三系数修正方程。

二系数修正的数学模型为

三系数修正的数学模型为

式中:V 为修正后的能见度值;a，b，c 是修正系数;σ 为消光系数。还可具有更多修正系数，修正系数越多越精确但计算越复杂。采用二系数修正方程对估算的能见度值进行修正，并将该式引申为大量采样点数据的线性拟合。根据能见度V 与消光系数σ 的反比关系，式(1)可变形为

式中:Vc是未经修正的仪器/装置测得的能见度值。

以二系数修正方程为例，假设仪器的修正或标定能够溯源到能见度的真值，将两对测得的能见度值与标准能见度的实验数据，代入二系数修正普遍数学模型，可建立一个以a，b 为未知量的二元方程组。解此方程组，可简便求得修正系数a，b。将修正系数回代入二系数修正普遍数学模型，便得到二系数能见度修正计算公式。

由于缺乏能见度所谓的标准值，一般都是参考所谓的标准仪器算得的能见度值来替代能见度真实值，而参考仪器本身存在一定的测量误差。因此，可以在参考仪器的测量范围内，实际测量获取更多对实验数据，将二系数或三系数修正推广至大量数据的多项式拟合。其基本形式为

当n = 1 时，式(4)即为式(3)。

2 测量实验与修正应用

用能见度测量装置和HY-VT100 (M)型透射仪进行测量能见度的比较实验，并进行装置的修正，见图1。参考仪器HY-VT100 (M)型透射仪的主要技术指标为:能见度测量范围2 ～10000 m，能见度小于2000 m 的相对误差在±5%以内，大于2000 m 的相对误差在±10%以内。大致选取满足本装置与参考仪器测量量程的条件，即约为十公里以内进行实验;选取环境稳定、不易受外界突发因素(如局部烟雾等)影响的地点;在保证测量光路互不影响的前提下，将本装置与参考仪器并排安置:两套基线平行，且本装置与透射仪接收机平行，反射棱镜与透射仪发射机平行。

图1 户外能见度测量实验

能见度测量装置与HY-VT100 (M)型透射仪测量能见度的比较实验曲线如图2 所示。测量装置的测量结果与参考仪器的最大偏差为2705.59 m，最大相对误差达到36.01%，不符合世界气象组织(WMO)对能见度测量误差≤±20%的规定［4］。

图2 未经修正的能见度比较曲线

对本装置进行二系数修正，选取实验中较长时间的稳定的能见度数值，同时满足HY-VT100 (M)型透射仪与本装置输出信号时间点对应的能见度值，依据修正方程式(3)，利用Matlab 对大量数据点进行拟合［5］，得到

将修正系数值回代到式(3)，则本装置的修正模型为

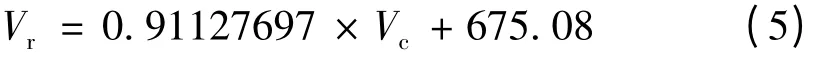
式中:Vc为未经修正的能见度值，m;Vr为经过修正的最终能见度值，m。

图3 经过修正后的能见度比较曲线

装置经过修正后的比较曲线，如图3 所示，可以看出装置与HY-VT100 (M)型透射仪测量的能见度更加一致，最大相对误差≤±14.1%。

3 其他拟合修正讨论

鉴于能见度测量值变化的离散性，而本装置与HY-VT100 (M)型透射仪之间测量趋势基本一致，故采用多项式拟合进行修正。二系数修正方程的本质即一阶多项式拟合，而三系数修正方程相当于二阶多项式拟合。为了探索修正的更好模型，或者验证二系数修正方程的合理性，依据式(4)进行二阶以及更高阶的多项式拟合数据处理。

以HY-VT100 (M)型透射仪测得的能见度值作为参考值，进行一至四阶拟合，计算残差

式中:ΔVi为第i 个采样点计算得到的残差;Vci，VHYi分别为本装置与HY-YT100 (M)型透射仪在第i 个采样点的能见度测量值。

求最大残差，并依据式(6)Bessel 公式［6］计算残差标准偏差估计值及相对误差，见表1。

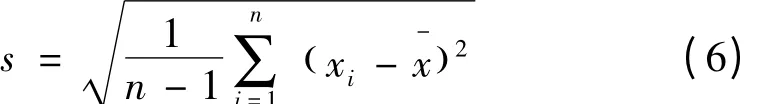
式中:s 为测量样本标准偏差。

表1 各阶修正模型残差对比

能见度的测量范围约为6 ～10 km，最大残差占测量范围的相对百分比(相对误差)小于15%。对比各阶拟合的残差，彼此之间差异很小。为了保证计算精度，拟合多项式的阶数一般不超过五阶，阶次太高，会使数据噪声也被纳入模型［5］。综上，采用一阶多项式拟合，即二系数修正方程已能够满足修正的要求。

4 比对实验

为了进一步验证多项式拟合的正确性，将式(5)作为修正的最终数学模型，进行本装置与HY －VT100(M)型透射仪的长时间比对实验。选取某次连续三天夜间能见度测量值绘成了连续曲线，如图4 所示。通过残差及相对误差的处理，得到各天数据结果如表2所示。表2 中，各天的残差分析中，能见度参考值用HY-VT100 (M)型透射仪示值替代。