商用车驾驶室横拉杆故障问题的试验研究及改进设计

李德光，韦志林

（1.东风柳州汽车有限公司技术中心，广西 柳州545005；2.广西工学院汽车工程研究所，广西 柳州545006）

目前的商用车普遍采用全浮式驾驶室以提高舒适性。为了减小驾驶室的侧倾运动幅度，在全浮式驾驶室后部设计安装了横向的拉杆装置（如图1所示），以提高驾驶室的侧倾刚度[1]。然而某型商用车在海南试验场进行可靠性试验时驾驶室横向拉杆发生了弯曲失稳变形、接头衬套断裂等故障现象。

图1 驾驶室横拉杆布置示意图

根据横拉杆的具体工作特点，该杆件在车辆在不平路面行驶时会承受来自两种驾驶室运动引起的载荷：其一是当驾驶室存在侧向加速度时横拉杆主要承受轴向的拉力或压力；其二当驾驶室绕X轴做摆动时会主要承受弯矩和扭矩。车辆在实际的行驶时往往是多种载荷同时出现，且这种在动态才会出现的载荷无法用静态计算进行分析，鉴于关于这方面的数据和相关的资料的空缺，进行相关的动态内力的电测试验并在试验基础上进行结构的再设计是有必要的。

1 横拉杆内力测试

通过电测试验测定横拉杆在可靠性路面上所受的应力和的内力（轴力、弯矩、扭矩），可以对横拉杆的强度做出评估，并对结构故障的原因进行分析，提出具体的改进意见。

1.1 内力测试原理

这里以一个受轴力和弯矩作用的箱形截面的梁的内力测量为例，说明用电测法测量内力的原理[2]。

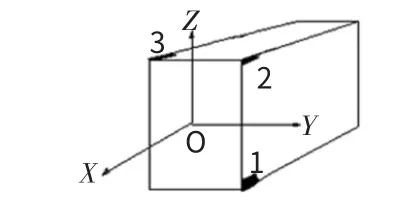
图2 轴力的内力测试

如图2所示，为了测量梁的受力，在梁的同一截面的3个位置布置了沿X轴方向的应变片。显然，应变片的测量值是梁所受轴力和弯矩共同作用的结果。这里规定若弯矩的矢量方向与相应的坐标轴方向相同则弯矩为正，与坐标轴方向相反则为负。因此，有如下等式成立：

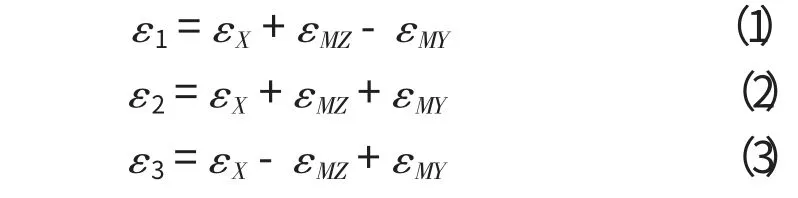
其中，

ε1、ε2、ε3为位置1、2、3处应变的测量值；

εX为由轴力引起的应变；

εMZ为由绕Z轴的弯矩引起的应变；

εMY为由绕Y轴的弯矩引起的应变；

ε1、ε2、ε3的值可以由测量仪器中读出，然后求解(1)、（2）、（3）式组成的方程组有：

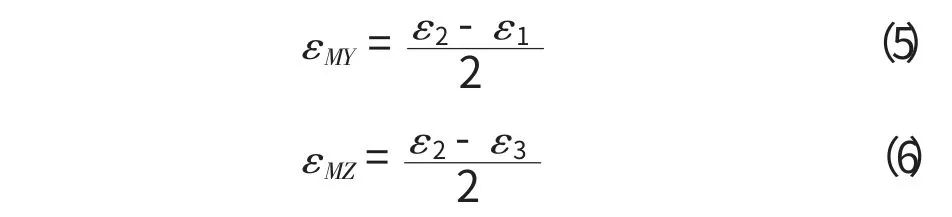
由材料力学知，轴力和弯矩引起的应变可以按式（7）、（8）计算：

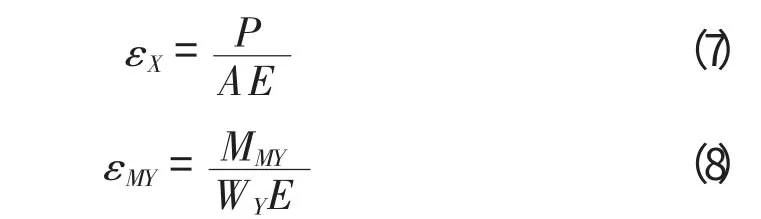
其中，

P为杆件所受的轴力；

A为杆件的横截面积；

E为杆件材料的弹性模量；

MY为矢量方向平行于Y轴的弯矩；

WY为绕Y轴的抗弯截面模量。

将它们分别代入（4）、（5）、（6）得到：

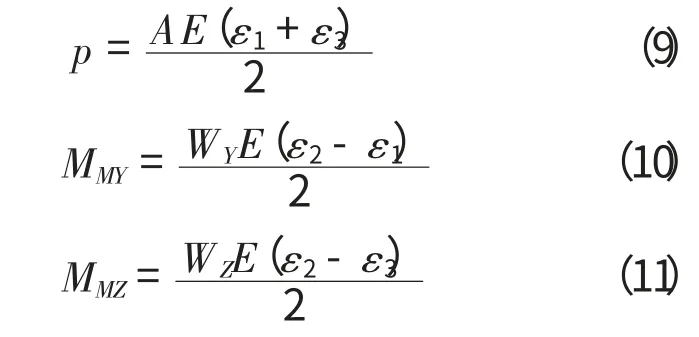
上述推导说明了轴力和弯矩的测量原理，对于扭矩等其它形式的内力也可以采用类似的方法加以测量。

1.2 测试对象惯性参数的计算

原杆件采用的是2 mm厚度的空心轴，其尺寸如下：

内径d=18 mm，外径D=22 mm，截面积：

1.3 测点布置

为测定横拉杆所受的应力和内力，需要在横拉杆的中部和两端布置测点。由前述的内力计算公式可知，轴力的计算结果对测量的应变值的变化比较敏感，测量误差对轴力有放大作用，测量误差产生的原因有横拉杆尺寸公差、应变片电阻误差、应变片贴片位置方位误差、测量时温度变化影响、仪器不稳定产生误差等因素。因此在未知弯矩、轴力、扭矩大小的情况下，本次实验在多个截面上布置测点，这样可以对计算出来的内力进行比较核对。

在布置测点时，按轴力、弯矩、扭矩的测试方法进行，测点布置方案如图3所示。各组测点的用途如下：

（1）测定1、2、3、4用于测定接头附近的应力。由于接头附近曾经出现断裂的现象，因此应变片的方位需与以前出现裂纹的方向垂直。

（2）测点6与8、14与16、18与20组成3组，用于测量3个截面处横拉杆所受的垂直弯矩。

（3）测点5与7、13与15、17与19组成3组，用于测量3个截面处横拉杆所受的水平弯矩。

（4）测点18与21、20与22组成两组测量横拉杆所受的轴力。

（5）测点9、10、11、12用于测量横拉杆的扭矩。

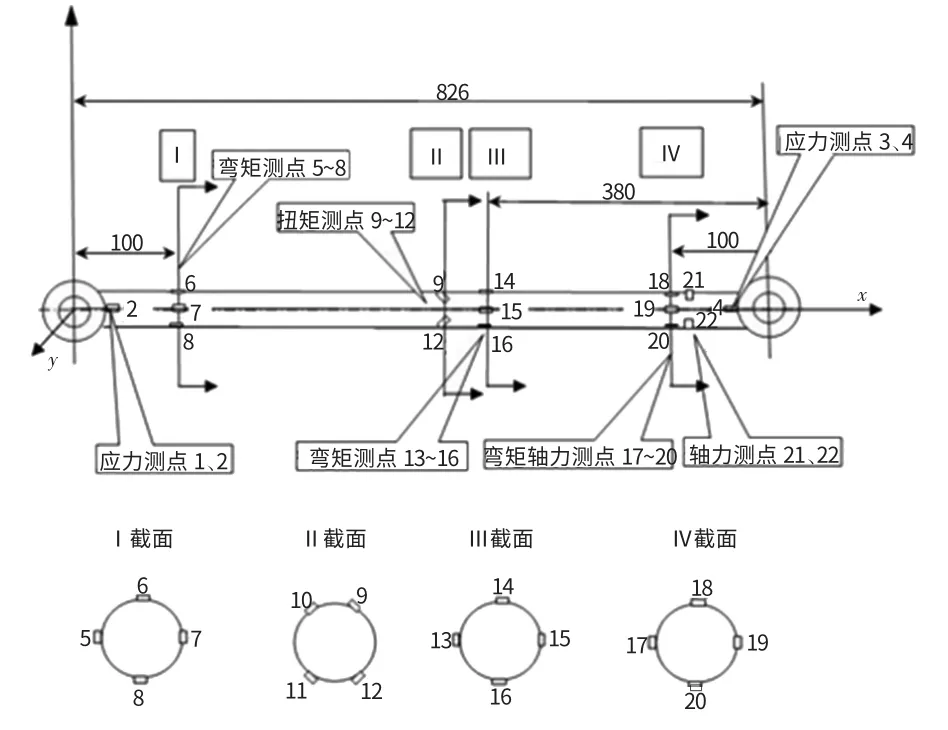
图3 测点布置示意图

1.4 测试数据

在海南汽车试验场可靠性跑道上进行实车测试，如图4为截面测点2的应变动态曲线。根据前述介绍的内力计算公式，计算出横拉杆在可靠性路面上所承受的载荷，如表1所示。

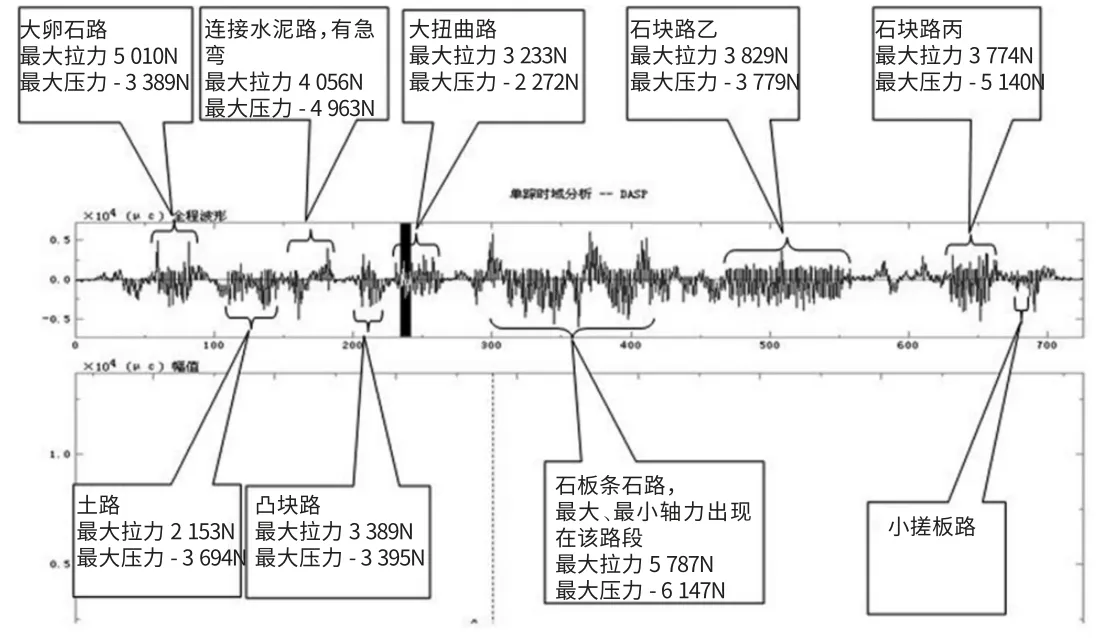
图4 测点2动态曲线及典型路段最大轴力数值

表1 各截面弯矩幅值统计

实验数据表明横拉杆主要承受的是轴力，弯矩和扭矩很小。

在同一截面选取不同的测点对计算轴力和弯矩所得结果略有不同，由于内力必须在测定应力的基础上经过相关的计算才可获得，而应变片的电阻值误差、贴片角度误差、构件尺寸误差，导线电阻值的误差都会对最终的结果造成影响。因此本次试验才在多个截面上电测试验，以获得较大轴力数据。

2 横拉杆失稳的屈曲有限元计算

屈曲分析主要用于研究结构在特定载荷下的稳定性以及确定结构失稳的临界载荷。线性屈曲分析是以小位移小应变的线弹性理论为基础的，分析中不考虑结构在受载变形过程中结构构形的变化，也就是在外力施加的各个阶段，总是在结构初始构形上建立平衡方程。当载荷达到某一临界值时，结构构形将突然跳到另一个随遇的平衡状态，称之为屈曲。临界点之前称为前屈曲,临界点之后称为后屈曲[3]。

利用hyperWorks结构设计分析软件包，建立横拉杆的有限元模型。模型中包含23 733个hex8实体单元，节点数为14 787。在横拉杆的一端施加铰链约束，在拉杆的另一端施加大小为10 N的轴向力，利用Optistruct求解器计算横拉杆的10阶失稳模态，结果如表2所示，失稳临界载荷为特征值与载荷的乘积。

表2 失稳计算结果

3 结构改进设计

对拉杆失稳的计算表明，对应2毫米厚度杆的失稳临界压力为5 166 N，试验所获得的2毫米拉杆最大轴压力为6 147 N，所以在车辆可靠性试验时拉杆发生了明显的失稳，失稳又直接导致应力的提高造成杆件高应力区的断裂。

由于空间布置的限制，现有的横拉杆外轮廓尺寸不能有明显的变化。为了提高该杆件的失稳临界载荷，将该横拉杆改为外径为φ22 mm、内径为φ14 mm，即厚度为4 mm的空心圆管。

经计算，改进后的横拉杆一阶失稳临界载荷提高为9 720 N，较原设计方案增加了88%。由于驾驶室的连接结构并没有变化，因此工作时横拉杆的最大轴向压力不变，改变横拉杆厚度后，该结构的失稳安全系数为9 720/6 147=1.58。

为了验证新尺寸横拉杆的可靠性，在海南试验场重新进行了可靠性试验，没有出现前述的各种故障。该车投入市场后也没有发生横拉杆断裂的情况，证明改进是有效的。

4 结束语

故障问题的成功解决表明我们关于横拉杆失稳的分析与实际情况符合，不仅解释了拉杆结构失效的机理，同时测定出实际的内力大小、幅值的统计等。这些数据对认识驾驶室实际工作状态是必不可少的资料，填补了公司驾驶室设计相关数据的空白，对今后的设计工作有实际的参考和借鉴的意义。

[1]叶福恒，许 可，等.某商用车驾驶室全浮式悬置系统开发[J].汽车技术，2010(06):33-39.

[2]吴宗岱，袁礼平.应变电测原理及技术[M].北京：国防工业出版社，1982.

[3]李楚琳，张胜兰，等.Hyperworks分析应用实例[M].北京：机械工业出版社，2008.