高填充细观模型不确定性及其表征*

姚 东，高 波，杨月诚，史宏斌

(1第二炮兵工程大学，西安 710025;2中国航天科技集团公司第四研究院第41所，国体火箭发动机燃烧、热结构与内流场国防科技重点实验室，西安 710025)

0 引言

针对颗粒填充/增强(韧)复合材料的细观模型，高希光[1]、宋玉普[2]、邵军超[3]等分别在陶瓷基复合材料、混凝土材料、颗粒增强金属基复合材料上开展了大量工作。宋卫东[4]研究了圆形颗粒填充的分子动力学方法，赵玖玲[5]基于最小碰撞时间探讨了椭球体形状参数的控制。宋卫东[4]、赵玖玲[5]等采用SEM结合数字图像处理技术分别对钨合金、混凝土及固体推进剂开展了细观模型的研究。侯善芹[6]等在双尺度分析的框架下对一定条件下颗粒数目、胞元尺寸等的影响进行了研究。姜芳[7]、Brassart[8]等基于Mori-Tanaka理论和Eshelby等效夹杂理论考虑了颗粒与基体之间粘接界面的脱粘，魏高峰[9]等则借助有限覆盖技术和改进的Voronoi单元对同类问题进行了研究。

从现有文献报道来看，建立细观模型一般有近似法(顺序法、并序法等)以及直接法两大类。对于近似方法，如果不考虑颗粒填充过程中重叠检测、取向等细节，填充、构造的最终效果均可以等效为对既有颗粒样本的放置。很明显，细观结构存在以下两个层次的不确定性:满足指定规则时，颗粒总数不确定;满足指定规则且颗粒总数一定时，颗粒分布、取向等不确定。对于具体的计算过程而言，还存在计算胞元的尺寸问题。

侯善芹[6]针对30%含量颗粒材料开展的均匀化分析和数值研究表明，颗粒随机分布时宏观等效模量是正态分布的，且所取体胞尺寸与颗粒尺寸之比越大，模量越集中在样本均值的小领域内;并指出胞元尺寸L存在与体积分数有关的临界值，大于该值后初始模量趋于稳定。Drugan针对大小为R的颗粒的研究表明，该临界值为 L/R=5。赵玖玲[5]采用双尺度方法针对复合固体推进剂的研究则表明，对于给定的体胞，填充颗粒越多，正态分布的初始模量概率密度的带宽越窄。总体来看，相比于均匀化等宏细观统一分析方法的全面工作，细观结构不确定性的系统研究尚未见报道。

文中以高填充分数的固体推进剂为背景，研究了球形颗粒填充细观结构的约束不完整性，提出了颗粒空间分布差异的子域形心表征方法。

1 体积填充/质量分数及粒径分布的约束不完整性

设单相增强颗粒半径服从正态分布，即r～N(μ，σ2)，则体积填充或质量分数的要求为:

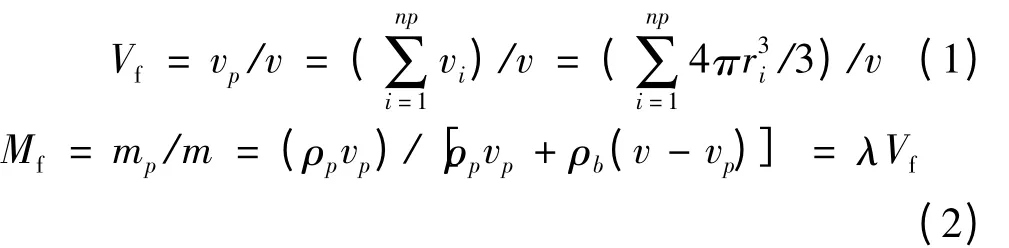
随机样本的二重性表明Vf是随机变量。计算了不同粒径规格下颗粒总体积vp与颗粒总数目np。vp可拟合为np的线性函数，但均存在局部的“涨落”。

1)相同均值μ下，满足相同体积分数所需的颗粒数(拟合值)随σ的增大而减小。设满足Vf=vp/v的np线性拟合结果为，对于 v=1、μ 为 0.1、σ 分别为0.01/0.05的情况，满足体积分数0.6所需分别约140/75。

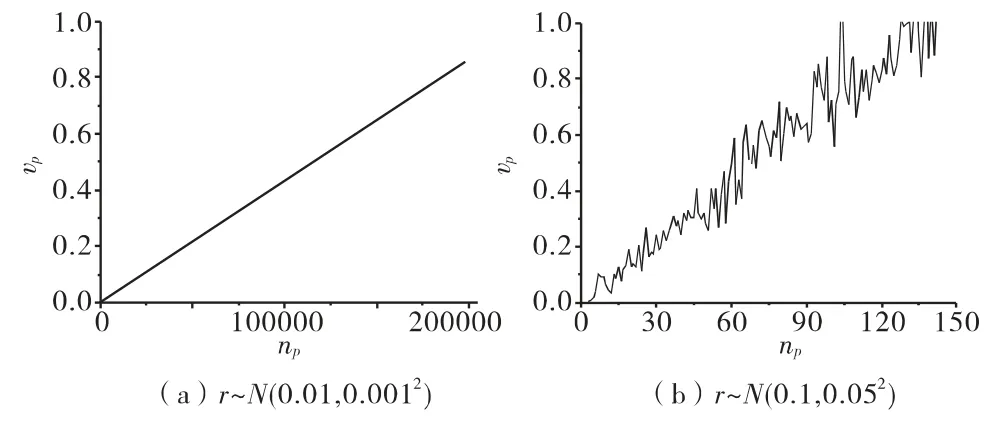
图1 线性拟合与局部“涨落”

2)局部“涨落”导致满足一定体积分数的颗粒数目不唯一。以Vf=vp/v=0.60为例，考虑有效位数取舍，r ～ N(0.01，0.0012)时颗粒数目从 138000 ～140000均可满足，r～ N(0.1，0.052)时颗粒数目则在60～90之间。

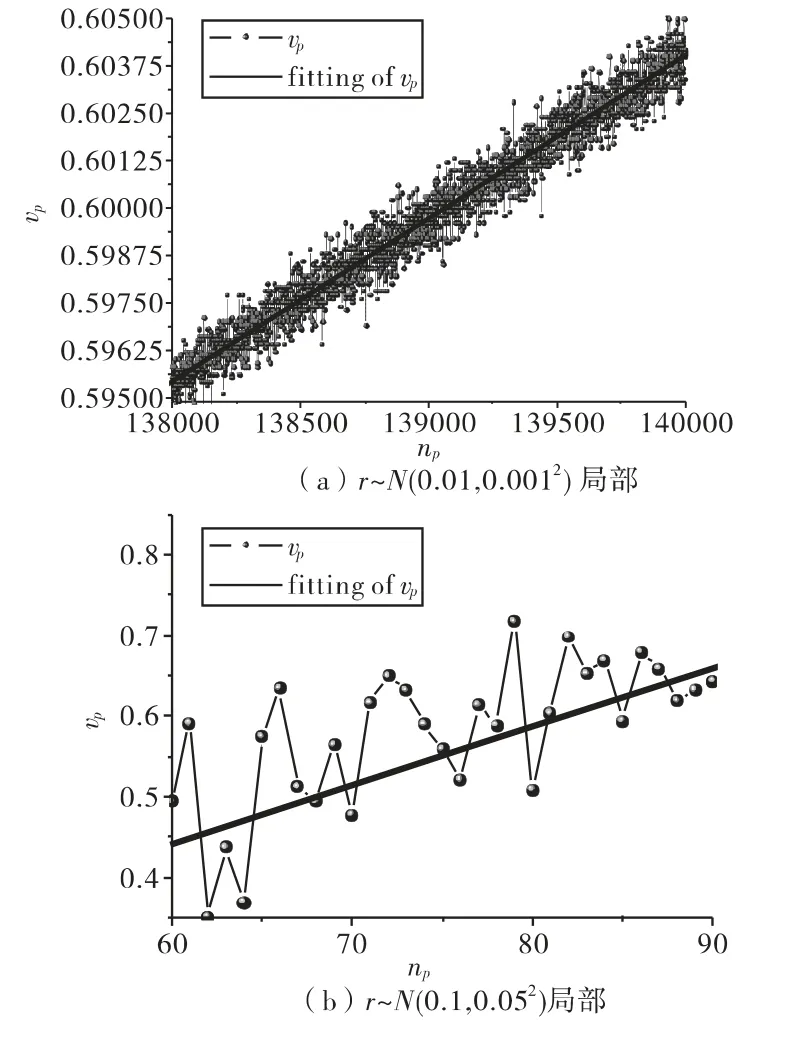
图2 整体线性关系与局部“涨落”

2 颗粒空间分布不确定性及其表征

设细观构型I、II存在图2所示的局部差异:I、II中填充颗粒数目、尺寸均一致，除了微元dΩ、dΩ'在I、II中分布位置有差异外，其余颗粒的分布、微元内部的颗粒分布、两微元的形状均一致。设 I、II参考坐标重合后dΩ、dΩ'形心之间的矢量为D。

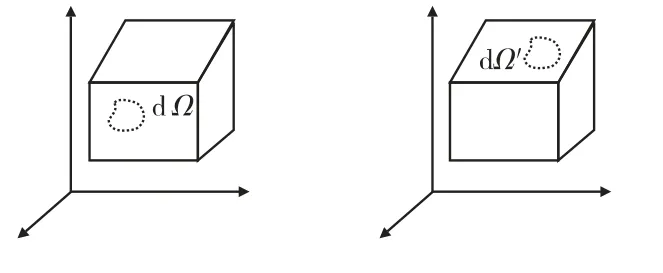
图3 细观构型的局部差异

如不考虑热应力等其它因素，上述差异可以通过dΩ与dΩ'的位置互换来实现。在dΩ或dΩ'足够小时，构型I、II的应力/应变仅在其相应位置及附近领域内存在差异，从而对整体的性能产生一定的、有限的影响。

填充颗粒数目及粒径均一致、填充分数较高时，构型I、II结构差异的直接描述是非常困难的。考虑到质量的分布是构型的直观反映，文中发展了子域形心表示方法。

设存在独立于胞元的网格将胞元划分为n个互不重叠的、单联通的子域，m个颗粒的球心落入子域Φi内，设其形心设为r(i)，则有:

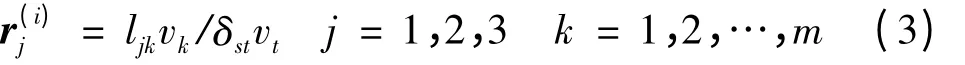
式中:ljk为Φi内颗粒k的形心在整体坐标轴j方向的分量，vt为颗粒的体积(t=1，2，…，m)。当各子域均只包含1个颗粒时，r(i)即为描述颗粒位置的坐标。

3 Matlab/Abaqus统一的分析平台及算例

3.1 Matlab/Abaqus统一的分析平台

由于增强颗粒的形貌、大小、取向等均存在随机性，相比于三维四向、针刺4D编织等结构几乎固定不变的三维 /二维编织复合材料，运用渐进展开与摄动求解颗粒增强复合材料的数学要求较高且效率较低。能量法在特定边界条件下探讨胞元变形能与均质等效体变性能的关系，结合有限元技术建立了简洁、高效的等效性能预测方法。

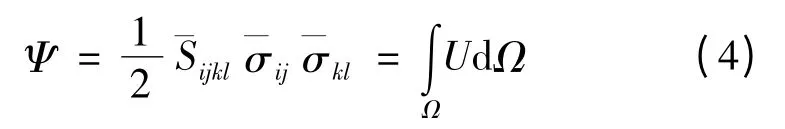
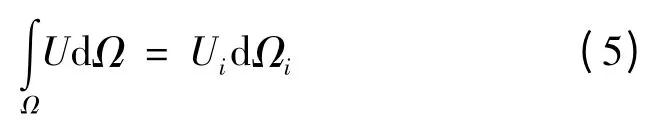
在Matlab平台下开发了顺序法填充生成细观模型的算法，集成了约束强化、颗粒生成、三维填充、子域划分 /断层扫描等功能;Python脚本文件导入颗粒尺寸及填充位置数据文件，生成Abaqus的.cae文件并提取预制集合的输出信息;返回Matlab平台下按能量等效对等效初始模量进行求解。

3.2 算例——颗粒空间分布不确定性对初始模量的影响分析

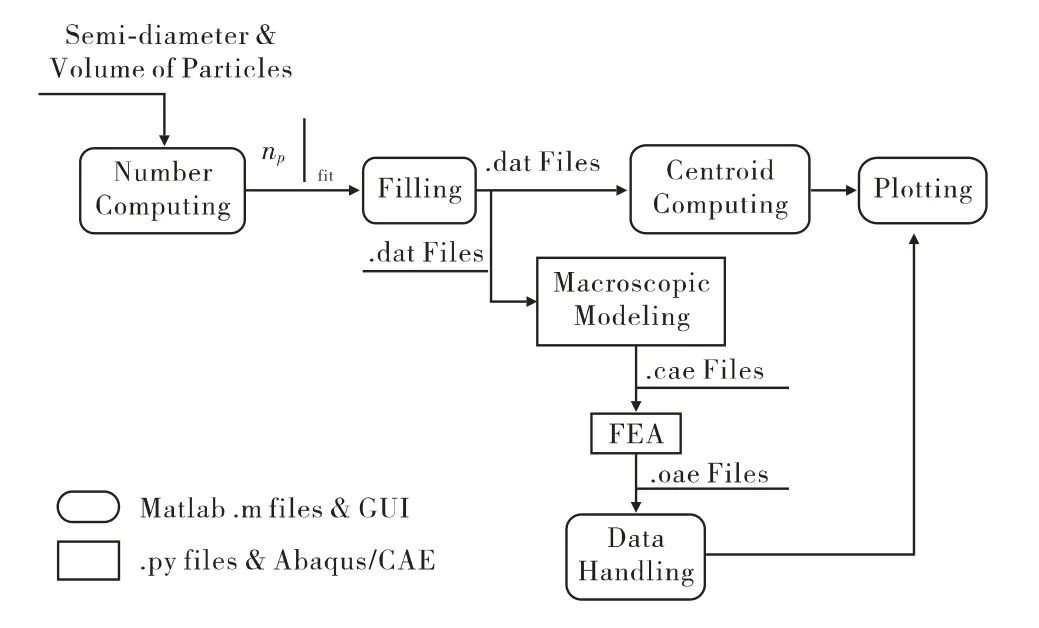
图4 分析平台的结构

初始模量 E 呈正态分布，μE为 19.73EB，σE为0.20EB，EB为基体模量。取背景网格为2 ×2 ×2(分胞元为8份)，[rij]规模为8 × 3。对 E 分别为19.96EB、19.62EB的模型2、模型19，均按式(3)处理，图像对比见图6。

图5 拉伸方向的应变云图

图6 差异对比

4 结论

文中以固体推进剂为背景，研究了颗粒填充细观结构的不确定性，提出了两个层次不确定性的表征方法。算例表明:

1)对于粒径服从正态分布的球形颗粒，填充分数是不完整的约束，随机样本的二重性决定Vf是颗粒数目的随机变量，颗粒总体积vp可拟合为颗粒总数目np的线性函数，但存在局部的“涨落”。对于固体推进剂，由于其颗粒组分体积分数高、粒径小，np的不确定性更为明显。

2)在给定颗粒数目的强化约束条件下，子域形心法结合图像表示可以有效表征颗粒空间分布的不确定性，随机生成的模型会导致初始等效模量的正态分布。

[1]高希光，宋迎东，孙志刚.陶瓷基复合材料高精度宏细观统一本构模型研究[J].航空动力学报，2008，23(9):1617－1622.

[2]宋玉普.多种混凝土材料的本构关系和破坏准则[M].北京:中国水利水电出版社，2002.

[3]邵军超，刘越.颗粒增强金属基复合材料力学行为有限元模拟研究现状[J].材料导报，2007，21(9):111－115.

[4]宋卫东，王静，刘海燕.颗粒增强复合材料真实结构有限元建模[J].北京理工大学学报，2009，29(6):501－505.

[5]赵玖玲.复合固体推进剂力学损伤与细观损伤演化过程数值模拟[D].西安:第二炮兵工程学院，2010.

[6]侯善芹，刘书田.颗粒增强复合材料弹性性能的统计特征分析[J].科学技术与工程，2008，18(15):4078－4082.

[7]姜芳，宁建国.有界面脱粘时颗粒增强金属基复合材料的弹塑性性能分析[J].材料工程，2006(z1):366－373.

[8]Brassart L，Inglis H M，Delannay L，et al. An extended Mori-Tanaka method homogenization scheme for finite strain modeling of debonding in particle-reinforced elastomers[J]. Computational Materials Science，2009，45(3):611－616.

[9]魏高峰，冯伟，高洪芬.基于位移插值的Voronoi单元有限元方法[J].应用力学学报，2008，25(2):342－346.