超声速封闭通道内振荡的振幅特性*
2013-12-10贺永杰马高建
贺永杰,马高建
(中国空空导弹研究院,洛阳 471009)
0 引言
冲压发动机助推工作阶段,进气道形成一个封闭盲腔,在超声速气流的作用下,若没有进气道保护头罩,通道内将一直存在纵向低频高振幅的振荡现象;即使有进气道保护头罩,在头罩分离后正常转级前,也存在此振荡现象。这种高振幅的振荡可能造成通道内压强超过许用极限,造成发动机结构破坏,因此对其研究十分必要。
针对超声速通道内的振荡现象,Trapier等[1]研究了通道出口反压造成的进气道处于亚临界状态时的振荡。杨党国[2]等研究了通道侧壁存在封闭空腔时的高频自激振荡。而对通道出口封闭引起的低频振荡,白晓征[3]等数值模拟了进气道整流罩开启的非定常过程,孙振华[4]等研究了冲压发动机助推工作的动态特性,孟宇鹏[5]等研究了出口封闭超声速进气道内的振荡频率,郭善广[6]等对高超飞行器中封闭通道振荡问题的分析。
文中研究重点为超声速来流条件下封闭通道内的振荡,着重于其振幅特性的归纳分析。上述相关文献中,研究侧重于流动过程的动态模拟和振荡频率预估。文中将对某轴对称超声速封闭通道内的振荡现象进行非定常数值模拟,分析特征因素对振幅特性的影响,为冲压发动机设计提供参考。
1 物理模型及计算方法
1.1 物理模型
以一种轴对称封闭通道模型为研究对象,在通道入口前是一个斜锥,如图1所示。
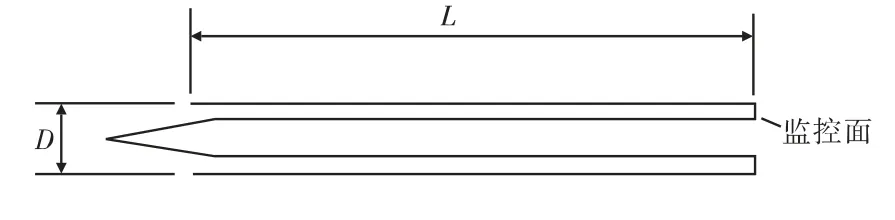
图1 封闭通道模型示意图
对于通道内振荡振幅的研究,主要考虑封闭通道结构和飞行状态的影响,其中通道结构选取长径比L/D为主要因素,飞行状态选取来流马赫数Ma为主要因素。取封闭通道结尾截面为监控面,计算在不同影响因素条件对振荡的影响,计算状态如表1所示。

表1 计算状态表
1.2 数值方法
计算中采用有限体积法求解雷诺平均后的轴对称N-S方程,如式(1)所示。
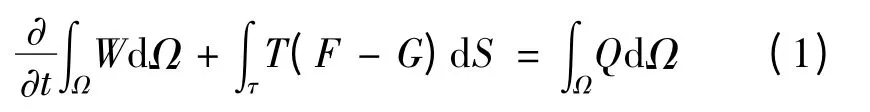
湍流模型选用标准κ-ε模型,对流通量采用二阶ROE格式进行离散,粘性项采用中心差分格式离散,瞬态项采用双时间步长推进求解。
计算中时间步长为10-6s。收敛准则为:连续方程、动量方程、能量方程、κ及 ε方程的残差下降3个数量级,且监控面的压强稳定。
2 计算结果与讨论
2.1 振荡现象及分析
以来流马赫数Ma=2.5、通道L/D=8的状态来分析封闭通道内的振荡现象。取监控面的面积平均压强来计算通道内的最大振幅。
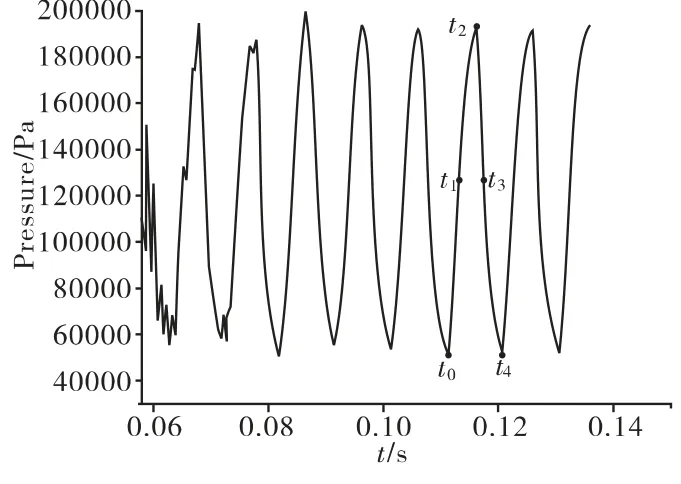
图2 监控面上压强随时间的变化曲线
图2给出了监控面上压强随时间的变化曲线。图3给出了一个振荡周期内典型时刻通道入口处的马赫数等值线图谱。
将一个振荡周期分解为几个典型时刻,从图3可以看出,t0~t1时刻,锥面上气流分离产生的强斜激波向通道入口靠近,通道内为亚声速流,通道尾端压强上升;t1~t2时刻,斜激波继续向入口移动,在t2时刻激波几乎封口,通道上唇口也产生一道向内的斜激波,通道内局部出现超声速流,通道尾端压强达到最大值;t2~t3时刻,来流能量已不能维持继续向通道内充气,通道内的高压气体开始向外排出,流出的气体在通道入口外迅速膨胀,将锥面上的强斜激波向远离通道入口方向移动,并形成一道几乎脱体的强弓形波;t3~t4时刻,由于通道内压强的降低,排气压强已不能维持,弓形激波向通道入口方向移动,并退化为强斜激波。
在图2、图3中,可以看出两个重要特征:一是,振荡的压强峰值接近来流总压,这表明通道尾端的压强并不取决于激波系和流动的损失,振荡系统具有能量调节作用;二是,在尾端压强达到最大值时,入口的激波还未被推出,约 1/4个周期后,入口锥面处才出现压强峰值,这表明通道尾端压强振荡和入口前锥面的压强振荡存在约1/4周期的相位差。
分析其机理,认为对此封闭通道所形成的振荡系统来说,来流空气是自振的能量源,封闭通道本身即为振荡装置,出口堵盖是压力波反馈装置,通道入口前锥面处的激波系 /附面层系统是能量调节装置。因此,对于这种自激振荡系统,激波系 /附面层的能量调节补偿作用是在整个振动周期内进行的,在一个周期的不同阶段,有时能量补偿超过了系统自身的损耗,有时相反,故通道尾端的压强将接近甚至超过来流压强;但能量的补偿和损耗在一个周期内整体上得到平衡,故通道尾端的平均压强应与来流波系损失后的总压相当。
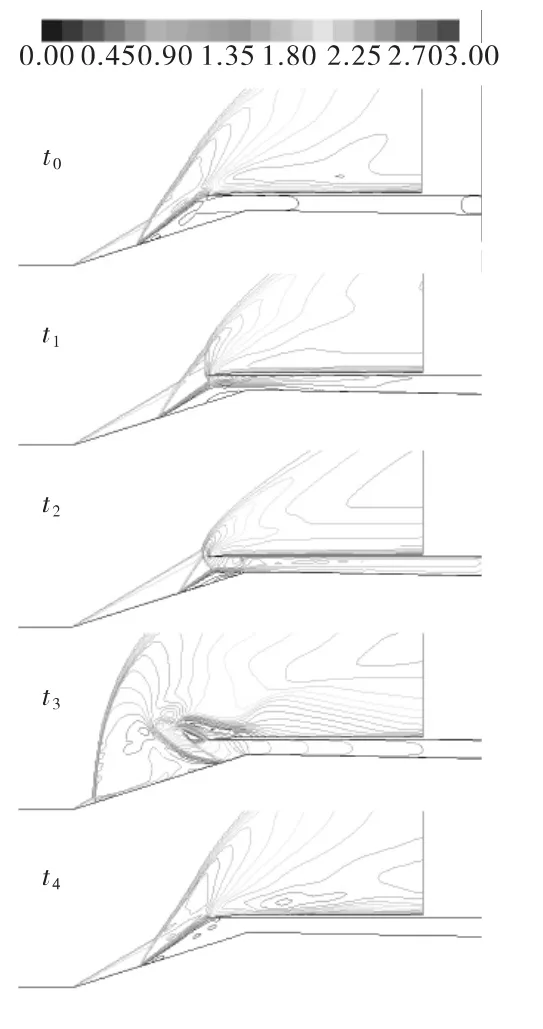
图3 一个振荡周期内典型时刻的马赫数等值线
2.2 振幅的变化规律
根据表1中各状态的计算结果,分析特征因素对振荡振幅特性的影响。
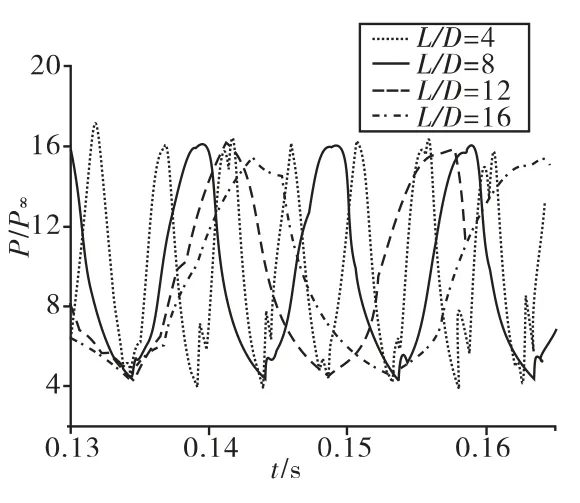
图4 不同L/D时的监控面上压比P/P∞随时间的变化曲线
图4给出了不同通道长径比L/D时,监控面上压比 P/P∞随时间的变化曲线。图5给出了不同来流马赫数 Ma时,监控面上压比P/P∞随时间的变化曲线。
从图4可以看出,在相同来流条件下,不同L/D时,通道内的振荡频率随通道长度的变化呈明显的线性关系,而振荡幅度△P和压强极值Pmax、Pmin基本不变,即通道内振荡的振幅与 L/D无关。
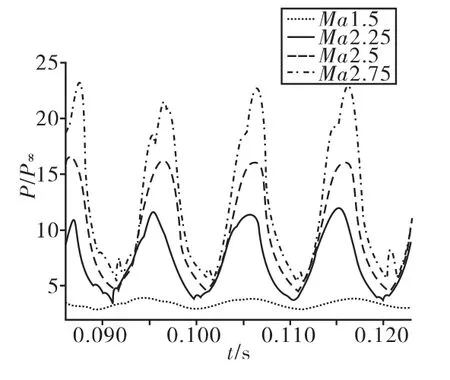
图5 不同马赫数时的监控面上压比P/P∞随时间的变化曲线
从图5可以看出,在相同几何条件下,不同马赫数 Ma时,通道内的振荡频率随Ma不同略有变化,这主要是由通道内当地声速的变化引起的。而振荡的绝对幅度 △P、压强最大值Pmax随Ma提高而大幅增加,压强最小值的Pmin增加相对平缓。
分析认为,由于封闭通道本身仅为振荡装置,它影响来流总能量的注入,也不能调节振荡系统能量的分配,因此不同通道长径比L/D对振荡的振幅影响很小,而随着来流马赫数增加时,由于系统注入的总能量大幅增加,因此压强振荡的绝对振幅大幅增加。
图6给出了在不同马赫数Ma时,通道内压强极值Pmax、Pmin随自由流总压变化曲线。
从图6可以看出,随着自由流总压的提高,通道内压强极值 Pmax、Pmin近似呈近线性升高,且振幅逐渐增大。也就是说,随着来流能量的增加,在同一种结构形式下,振荡系统能量的调节分配不变,故压强极值增加近似为线性。

图6 压强振荡的极值随自由流总压的变化曲线
在不同马赫数Ma时,图7给出了监控面压强与自由流总压之比随时间的变化曲线。图8给出了通道内压强与来流总压之比的相对极 值、、平均值以及通道前正激波后总压随马赫数变化的规律。图9给出了通道内压强振荡与来流总压之比的相对振幅随马赫数的变化规律。

图7 不同马赫数时的监控面上压比随时间的变化曲线
从图7可以看出,在一定来流条件下,通道内压强振荡的最大值Pmax将超过来流总压且压强振荡的相对振幅有变化。
从图8中可以看出,当来流 Ma小于约2.3时,通道内振荡的压强峰值Pmax将超过来流总压,且随着马赫数的降低,超过总压的幅度越大。而通道内振荡的平均压强 Pmean与来流在通道入口正激波后的总压P'*很接近。
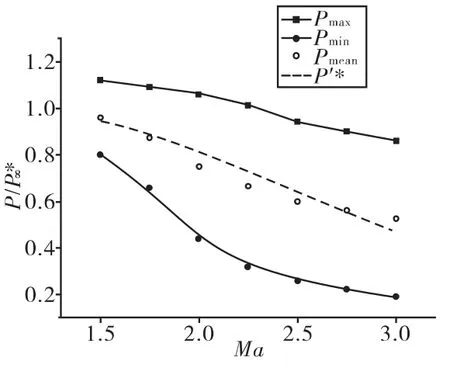
图8 压强振荡的相对极值随马赫数的变化曲线
从图9中可以看出,在 Ma大于约 2.0时,通道内压强振荡相对于来流总压的振幅基本保持不变,≈0.65;在Ma小于约2.0时,振幅急剧下降。
分析认为,作为一个自激振荡系统,其振荡本身的阻尼很小,因此在封闭通道尾端的平均压强Pmean与能量输入端的平均压强相当,而输入段的平均压强可近似认为是来流正激波后的总压P'*。在平均压强的基础上,振荡调节系统决定了压强的极值,如前所述,振荡系统的补偿使得通道尾端压强峰值Pmax可能超过来流总压P*∞。在通道入口锥面不变的条件下,随着来流马赫数小于一定值之后,所形成激波系 /附面层系统不同,即振荡系统调节机制不同,造成目前研究的方案中,在Ma小于约2.0时相对振幅△P/P*∞快速下降。
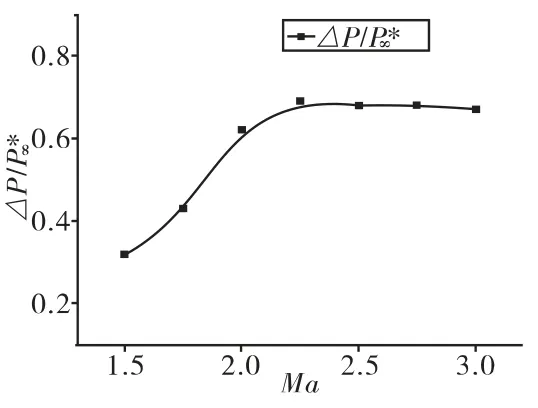
图9 压强振荡的相对振幅随马赫数的变化曲线
3 结论
1)在超声速条件下,封闭通道本身形成一个自激振荡系统,通道内振荡的平均压强约为波后总压,振荡幅度与来流马赫数和入口前的激波系/附面层系统相关;
2)在一定的封闭通道长径比范围内,通道内振荡的极值和振幅与通道长径比无关;
3)在一定超声速范围内,随着马赫数的升高,通道内压强振荡的最大值和最小值随总压接近线性增加,振荡的绝对振幅增大,与来流总压之比的相对振幅趋于不变。
[1]Trapier S,Deck S,Duveau P,et al. Delayed detached-eddy simulation of supersonic inlet buzz,AIAA 2007-4353[R].2007.
[2]杨党国,范召林,李建强,等.超声速空腔流激振荡与声学特性研究[J].航空动力学报,2010,25(7):1567-1572.
[3]白晓征,刘君,郭正,等.冲压发动机进气道压力振荡过程的数值研究[J].推进技术,2008,29(5):562-565.
[4]孙振华,吴催生.冲压发动机加速阶段进气道内动态特性[J]. 固体火箭技术,2011,34(3):285-289.
[5]孟宇鹏,朱守梅,闫晓娜.出口封闭的冲压发动机进气道激波振荡现象[J].推进技术,2011,32(5):606-610.
[6]郭善广,柳军,金亮,等.高超飞行器内流道激波振荡问题的数值研究及试验验证[J].实验流体力学,2012,26(1):7-11.
