非正常着靶弹体结构动力学响应数值仿真*

杨晓红，韩珺礼，徐豫新，唐 宏

(1 63961部队，北京 100000;2北京理工大学爆炸科学与技术国家重点实验室，北京 100081 3国营743厂，太原 030051)

0 引言

弹药作用时可能因机械故障等原因无法实现既定的战术功能和作战使命，为了不将失效弹药的内部构成等秘密泄漏给敌方，往往通过在战斗部处加装自毁装置实现非正常作用弹药的自毁。弹药自毁装置设计时通常需要回答1个问题:自毁装置的启动过载阈值是多少?该问题的回答若通过试验获得消耗大、周期长，且难以穷举所有非正常作用情况，在工程实践中可操作性差，新技术途径的提出有着强力的现实需求。通过试验获取正常着靶条件下弹体结构动力学响应数据，标定数值仿真用材料模型、参数和算法，通过同参数设置条件下数值仿真研究弹体非正常着靶条件下的动力学响应特征，分析极端条件下弹体非正常着靶的过载信息，并以此为基础设置自毁装置的启动过载阈值，可为弹药自毁装置的设计提供技术支撑。已有弹体结构侵彻过程中的数值模拟研究多关注大长径比弹体的结构强度[1－2]，为弹体结构的形状和强度设计提供帮助，通过数值仿真研究弹体非正常着靶状态下自毁装置的启动过载阈值尚未见文献报告。

以典型杀爆火箭弹为例，进行非正常着靶弹体结构动力学响应数值仿真，获得发动机未正常分离全弹着地、发动机正常分离降落伞未及时打开带控制舱战斗部着地两种情况下战斗部处的最大过载，为火箭弹自毁装置启动过载阈值的设定提供参考和借鉴。

1 数值仿真模型

1.1 模型假定

在研究中，首先对结构进行如下假定:

1)同一种材料内任一点在各个方向上具有相同的性质;

2)考虑各种结构的损伤、变形或破坏，结构破坏符合Von Mises强度准则;

3)炸药在侵彻过程中不考虑爆炸效应，仅将其与导弹壳体等部件一样看作侵彻体;

4)忽略空气阻力对导弹侵彻靶板过程的影响，在侵彻过程中，导弹仅受到土壤阻力的作用。

1.2 弹体等效模型建立

根据实际问题，建立相应的等效模型，并进行几何建模。对于杀爆弹丸侵彻典型土壤介质来讲，主要的研究问题是弹药不同着靶姿态在侵彻土壤介质过程中，弹丸整体与其分部件的动态力学响应及其结构特征的变化情况。通常杀爆火箭弹由控制舱、战斗部舱、伞舱、发动机舱，共4部分几百个零件构成。在数值仿真中难以把每个零件均建立出来。因此，针对所关注的结构整体动力学响应问题，在不影响数值仿真结果的情况下，对弹体结构进行等质量、等壁厚简化。根据弹丸外形几何尺寸，并依照各部分的质量特征，分别对上述舱段内部进行了配重处理，构建了一些相应的配重部件。通过简化获得典型杀爆火箭弹弹体结构如图1所示。

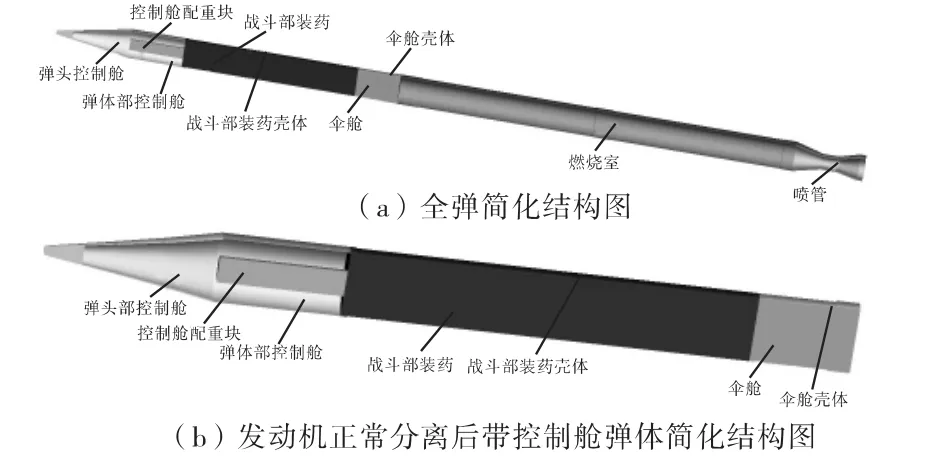
图1 典型杀爆火箭弹的简化模型

1.3 弹靶有限元模型

根据上述简化模型，采用 cm-μs-g-Mbar单位制，根据弹体的结构简化模型，通过TureGrid软件进行离散化建立弹体有限元模型如图2所示。同时，通过TureGrid软件采用网格疏密渐变方法，建立靶体有限元模型，如图3所示，整个仿真模型共划分有单元326833个，节点355737个。

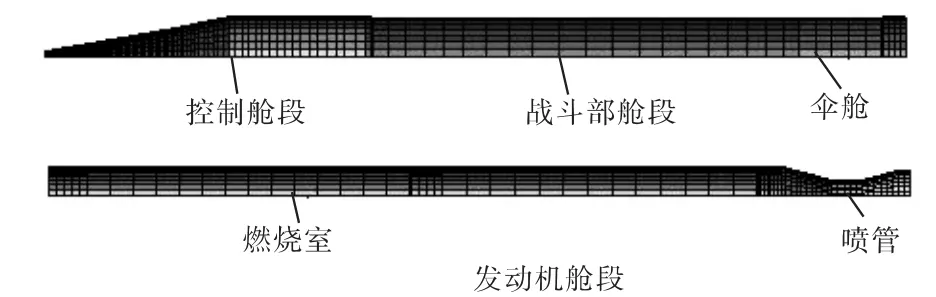
图2 全弹有限元模型

图3 靶体有限元模型

1.4 数值仿真用材料模型

弹体和靶板撞击所产生的现象与弹体撞击速度、撞击角度、弹体和靶板介质的形体和尺寸(特别是靶板厚度方向)、弹体和靶板的材料性能等有关。随着撞击速度由低至高，弹体和靶板材料依次发生弹性变形、塑性变形、流体弹塑性变形、断裂、甚至相变、粉碎、爆炸。由于所研究问题的速度不是很高，控制舱壳体、战斗部壳体、伞舱壳体、伞、燃烧室、喷管等均采用弹塑性随动硬化模型。此外，根据文献[4]土壤材料也可认为是塑性可压缩材料。根据文献[5]获得数值仿真用材料模型参数见表1。

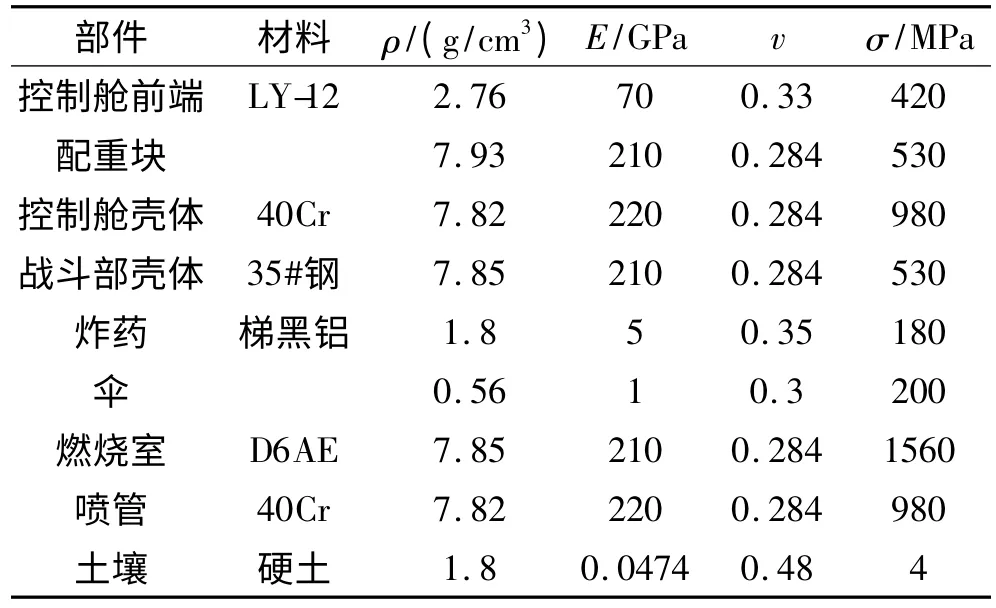
表1 材料模型计算参数

2 仿真结果及分析

2.1 正常着靶数值仿真

针对硬土，进行弹体正常着靶条件下90°落角的数值仿真，如图4所示。因自毁装置和战斗部壳体固联，通过调整仿真中的接触参数，获得战斗部壳体的最大过载为528g，与试验结果486g相差8.6%，表明数值仿真结果具有可靠性，通过仿真获得的各部分过载曲线如图5所示。

2.2 非正常着靶数值仿真

针对发动机未正常分离全弹着地、发动机正常分离降落伞未及时打开带制导舱战斗部着地两种情况进行弹体非正常着靶条件下的数值仿真，具体工况如下:

1)发动机未正常分离全弹着地:根据弹道分析确定发动机未正常分离条件下弹体以400m/s的着速，65°的落角着地;

图4 战斗部垂直着靶仿真模型

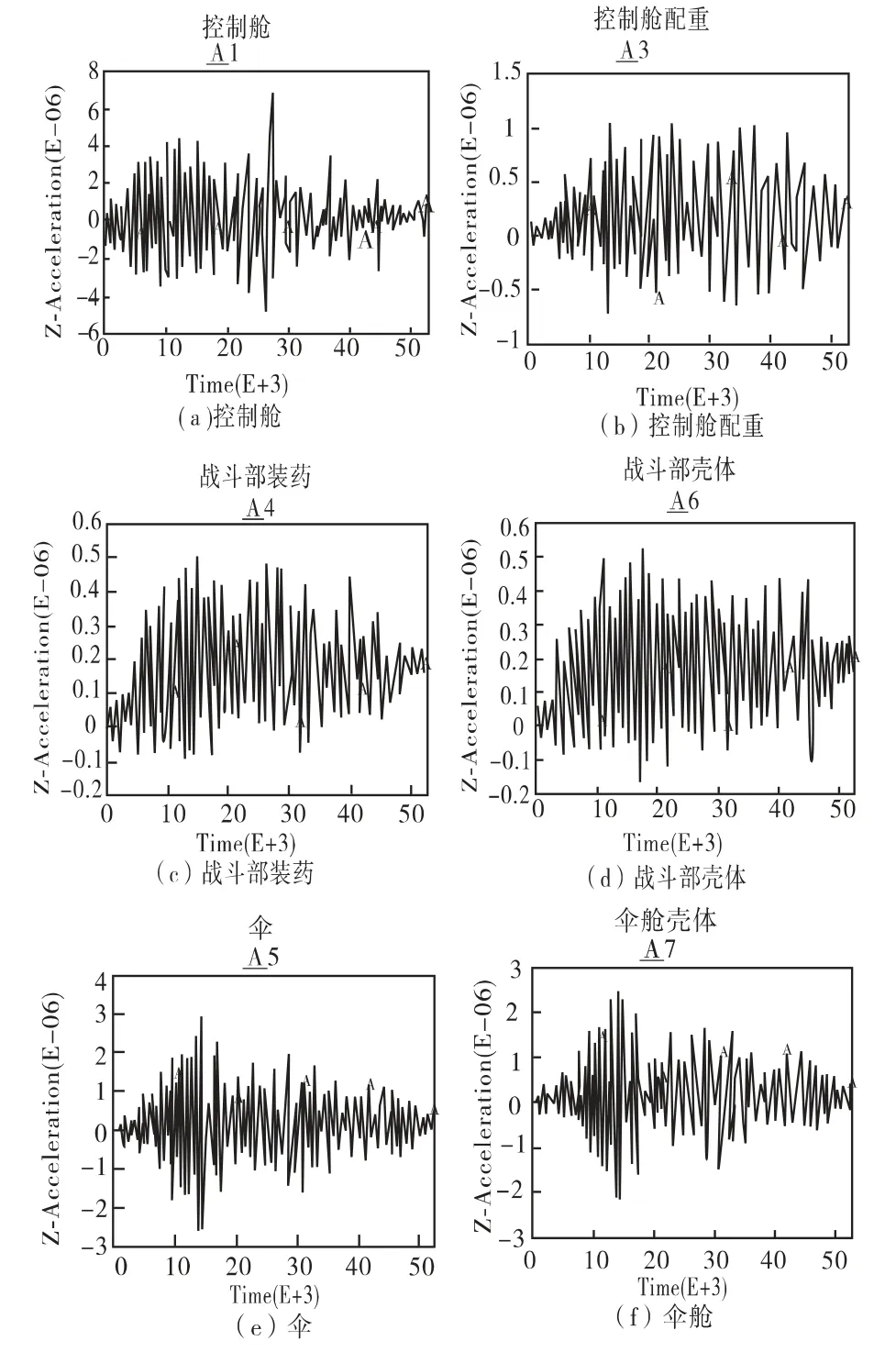
图5 仿真计算获得弹体各部分过载

2)降落伞未及时打开带制导舱战斗部着地:因可能出现带制导舱战斗部空中翻滚情况，选取水平、倒落两种极端条件仿真，通过弹道分析估算，弹体着速为100m/s。

根据上述工况，建立数值仿真模型如图6所示，采用上述仿真中的材料模型和接触控制参数进行计算。获得的典型计算结果如图7所示，获得战斗部壳体的最大过载列于表2中。

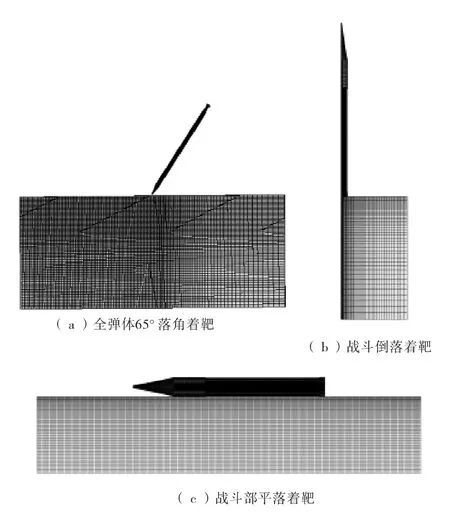
图6 仿真计算工况

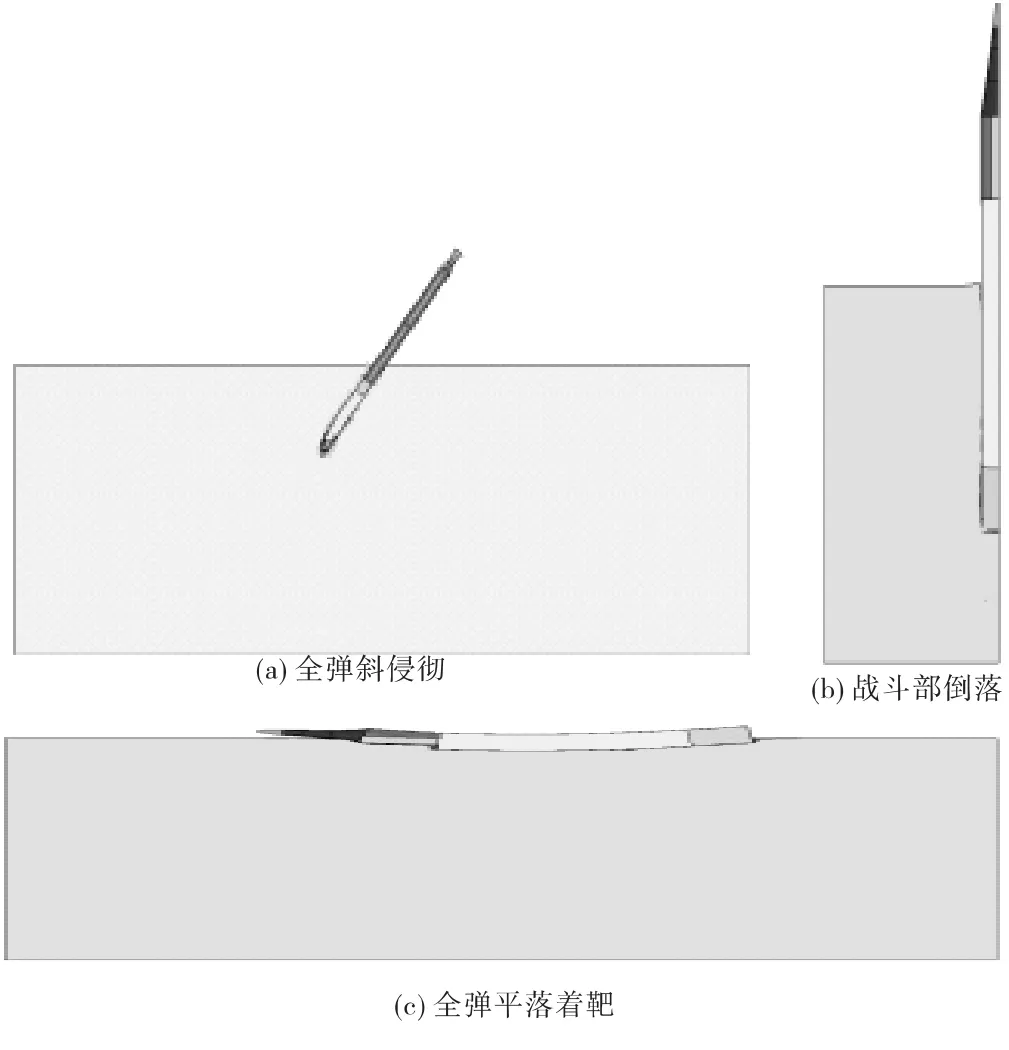
图7 典型计算结果

表2 不同工况下战斗部壳体的最大过载

根据自毁装置的功能，为保证自毁装置在弹体正常着靶时不作用，在非正常着靶时作用，自毁装置的启动过载阈值应大于弹体正常着靶作用时的过载值，小于非正常着靶作用时的过载值。根据表2中的仿真结果，自毁装置的启动过载阈值应大于528.0g，小于1465.0g，为提高可靠性，增加20%的余量。因此，可设定火箭弹自毁装置启动过载阈值在800～1000g之间，便可实现弹药失效后自毁的战术功能。

3 总结

自毁装置启动过载阈值设定关系到弹药在因机械故障等原因无法实现既定的战术功能和作战使命情况下的适时自毁，是弹药研制中的关键环节。但因弹药机械故障失效后多数情况下为弹体的非正常着靶，试验研究较为困难，且周期长、耗资大。文中采用数值仿真方法，通过弹体正常着靶试验数据标定数值仿真材料及接触控制参数，通过有限元仿真获得弹体非正常着靶情况下结构的动力学响应特征，并综合分析获得自毁装置启动过载阈值。该方法可为弹药自毁装置的设计提供技术支撑。

[1]徐培德，谭东风.武器系统分析[M].长沙:国防科技大学出版社，2001:94－150.

[2]皮爱国，黄风雷.大长细比弹体斜侵彻混凝土靶的动力学响应[J]. 爆炸与冲击，2007，27(4):331－337.

[3]皮爱国，黄风雷.大长细比结构弹体侵彻2024-O铝靶的弹塑性动力响应[J].爆炸与冲击，2008，28(3):252－259.

[4]时党勇，李裕春，张胜民.基于 ANSYS/LS-DYNA 8.1进行显式动力分析[M].北京:清华大学出版社，2005.

[5]才鸿年，赵宝荣.金属材料手册[M].北京:化学工业出版社，2011.