推移质输沙率计算公式分析

吴金萍，沙红良

（长江水利委员会水文局 长江下游水文水资源勘测局，江苏 南京 210011）

0 引言

推移质运动是全沙运动的一部分，它对山区性河流河床演变影响较大。 因此，提高推移质输沙率计算公式的准确性，对分析计算泥沙的输移意义重大。

关于推移质输沙率计算公式，前人分别从实验研究、量纲分析、统计理论和力学分析等方面开展了较多的研究。 如，刚恰洛夫、沙莫夫分别建立了以流速为主要参变数的推移质输沙率公式； 梅叶－彼德、恩格隆、阿克思－怀特等建立了以拖曳力为主要参变数的推移质输沙率公式；拜格诺、窦国仁从能量平衡观点研究推移质输沙率；爱因斯坦根据统计法建立推移质输沙率公式。 在这些已有的公式中，从力学方面研究的成果较多。 力学分析主要基于能量平衡的观点，认为泥沙输移的能量取自于水流能量，并假定泥沙输移所获得的能量与水流能量成比例，从而建立推移质输沙率公式。 基于力学分析所得到的推移质输沙率计算公式存在2 个问题：一是较少考虑推移质运动的滞后效应对推移质输沙率的影响； 二是推移质输沙率计算公式精度不够高，很难用于以悬移质为主要形式的输沙率和全沙输沙率的计算。

本文在现有推移质输沙率研究成果的基础上，根据推移质运动所需能量取决于推移质滞后速度的原理，建立推移质输沙率计算公式，并用较多的实验资料和实测资料对公式进行验证，最后分析了公式的计算精度。

1 推移质输沙率计算公式推导

1.1 输沙率计算公式表达式

在水流作用下，河床表面的泥沙以推移质形式运动。 由于水沙密度差异、推移质之间的相互摩擦和碰撞，以及推移质与床面相摩擦等原因，推移质运动一般滞后于水流运动。 就能量平衡观点而言，只有推移质与水流存在速度差，水流才有可能向推移质提供能量，也只有水流不断地向运动滞后的推移质提供能量，才能使泥沙处于推移状态。 因而，根据推移质输沙率定义及能量平衡观点，可建立如下能量平衡关系。

式中： ρ 为水的密度；ur为水流与推移质之间的相对速度；uf为水流作用流速；ub为推移质在水流方向的平均速度， 且ub=uf-ur；g 为重力加速度；qb为单宽推移质输沙率；a1为能量转换系数；τb为床面水流剪应力，τb=ρu2*，u*为水流摩阻流速； τc为临界床面水流剪应力，τc=ρu2*c，u*c为临界水流摩阻流速； U为水深平均流速。

根据实验研究，Francis（1973）得到推移质运动速度为

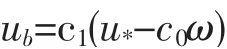
式中：ω 为泥沙沉降速度；c1为沉速系数，uf=c1u，c1＝6.0～10.5；c0为待定参数，ur=c0c1ω，c0＝0.032～0.056。

另一方面，推移质运动与近底水流作用流速之间存在一定关系，如Yang （1996）、Yang （2005）在分析推移质输沙率时指出，近底流速影响泥沙输移。若用近底水流作用流速代替式（1）中水深平均流速，设U=a2uf（a2为流速比例系数），并将ug=c1u*代入，可得推移质输沙率关系式为

式中：a0为待定综合参数，a0=a1a2c1/c0，其他系数意义同上。

式（2）即为推移质输沙率能量平衡模型，需要确定的参数为a0和c0。

1.2 参数确定

式（2）中，参数c0仅在泥沙刚运动时（u*略大于u*c）对推移质输沙率存在一定的影响。 当u*远大于u*c时，c0对推移质输沙率的影响较小， 可以忽略不计。因而，c0一般可取为常数。a0是通过比较a0与无量纲参数和的相关性，取相关系数较大的无量纲参数建立关系式。 本文采用Gilbert 和Zurich 的实验资料［1］对式（2）进行率定和验证。 资料包括3 种泥沙，分别是密度为4 220 kg／m3的重晶石、密度为2 650 kg／m3的沙砾和密度为1 250 kg／m3的煤粉。 重晶石的粒径为0.521 mm，沙砾的粒径分别为2.86 mm、0.521 mm、0.702 mm、0.172 mm、0.078 7 mm、0.037 5 mm 和0.031 5 mm，煤粉的粒径为0.521 mm。 通过实验资料反求a0，并计算前述3 个无量纲参数。 比较a0与前述3 个无量纲参数的相关性，a0与相关系数最大， 与的相关系数次之，与的相关系数最小，故选择为参数，建立a0的关系式。 a0与的拟合关系如图1 所示。

经数值比较，并参考实验结果，取c0=0.04 时，由图1 可建立a0的拟合关系式为

图1 u*/u*c 与a0 拟合曲线关系图Fig.1 u*/u*c and a0 fitted curve

上式的相关系数为0.43。尽管相关程度不高，但是由图1 可知，在1.0～5.0 的变化范围内，a0的数值变化范围为0.2～1.24， 对提高推移质输沙率计算精度具有一定的积极作用。

2 推移质输沙率计算公式验证及应用

2.1 公式验证

采用Gilbert 和Zurich 的实验资料对（2）式进行验证。 按照（2）式计算的单宽推移质输沙率qbc与实测单宽的推移质输沙率qbm进行比较， 比较结果如图2 所示。

图2 计算的单宽推移质输沙率与实测值比较图Fig.2 Comparison of the computational single-width bed load sediment discharge and real measured value

从图2 可以看出，无论是低输沙率，还是高输沙率， 计算的单宽推移质输沙率与实测值的相关性均较好，相关系数为0.82。

2.2 公式应用

对于悬移质而言， 泥沙的悬浮功来自水流的紊动能。 从数学关系的角度考虑ur∞ω 和δ∞h（h 为水深），式（1）左边项可以转化为悬浮功［C0(ρs-ρ)ghω］，右边水流势能等于水深平均的水流紊动能。 因而式（1）概括了推移质和悬移质输移规律，只要选择合适的参数， 所得的推移质输沙率公式可以适用于以悬移质为主要形式的输沙率和全沙输沙率的计算。 按照式（2）计算单宽输沙率，并与实验观测及实测单宽输沙率比较， 分析公式的应用性。 采用资料包括Simons（1960）［2］、Smart（1984）［3］、Stein（1965）［4］的 实验资料和长江下游大通水文站悬移质输沙率实测资料等。 Simons 实验资料中泥沙粒径为0.28 mm 和0.45 mm，在不同的水流（包括缓流和急流）和不同的床面形态（沙纹、沙垄、动平床和逆向沙垄）条件下，取得全沙输沙率实验资料。 Smart 实验研究了均匀沙 （平均粒径分别为4.2 mm、10.5 mm、2 mm 和4.3 mm）输沙率，实验水流条件特点为水流能坡较大，变化范围为0.03－0.20，得到输沙平衡的全沙输沙率实验资料。 Stein 测验水流和沙波运行要素，根据实验量测的沙波尺寸和运行速度，确定推移质输沙率。悬移质输沙率资料主要用长江下游大通水文站的实测资料。 计算以推移质为主要形式的输沙率和全沙输沙率qbc，与实验观测和实测资料的输沙率qbm比较，其结果如图3～图6 所示。

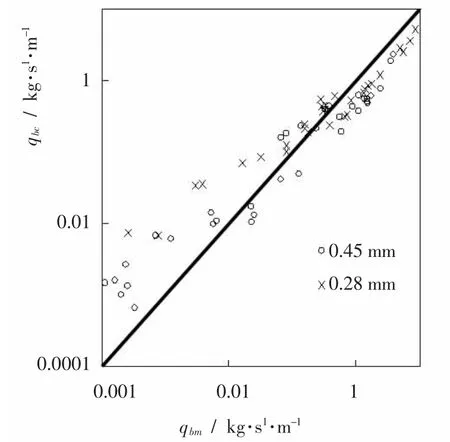
图3 计算的Simons 全沙单宽输沙率与实验观测值比较图Fig.3 Comparison of the computational Simons total sediment single-width sediment discharge and experiment observed value

图4 计算的Smart 均匀沙单宽输沙率与观测值比较图Fig.4 Comparison of the computational Smart uniformity sediment single-width sediment discharge and observed value

图3～图5 分别为根据Simons、Smart、Stein 实验资料计算结果与实验观测结果比较图。 从图3 中可以看出，用式（2）计算时，低输沙率计算值偏大些，高输沙率略微偏小些。 从图4 中可以看出，用式（2）计算的单宽输沙率从低到高均与实验值有较好的一致性。从图5 中可以看出，计算值与实验值的变化趋势比较一致，只是数据存在一定的分散性。图6 为长江下游大通水文站单宽悬移质输沙率计算值与实测值的比较， 计算的单宽悬移质输沙率与实测值相关性较好，但点据存在一定的分散性。

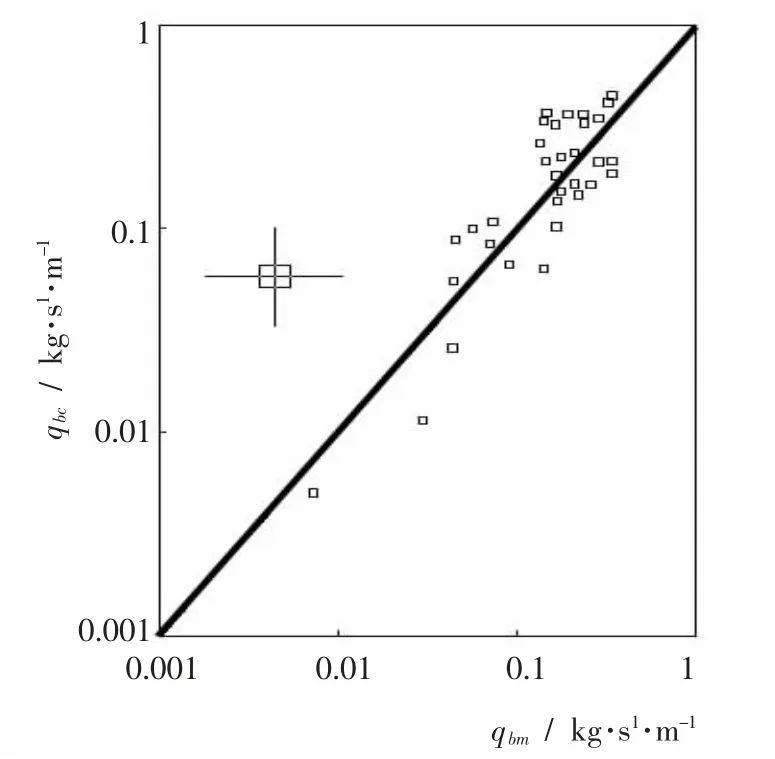
图5 计算的Stein 单宽推移质输沙率与观测值比较图Fig.5 Comparison of the computational Stein singlewidth bed load sediment discharge and observed value

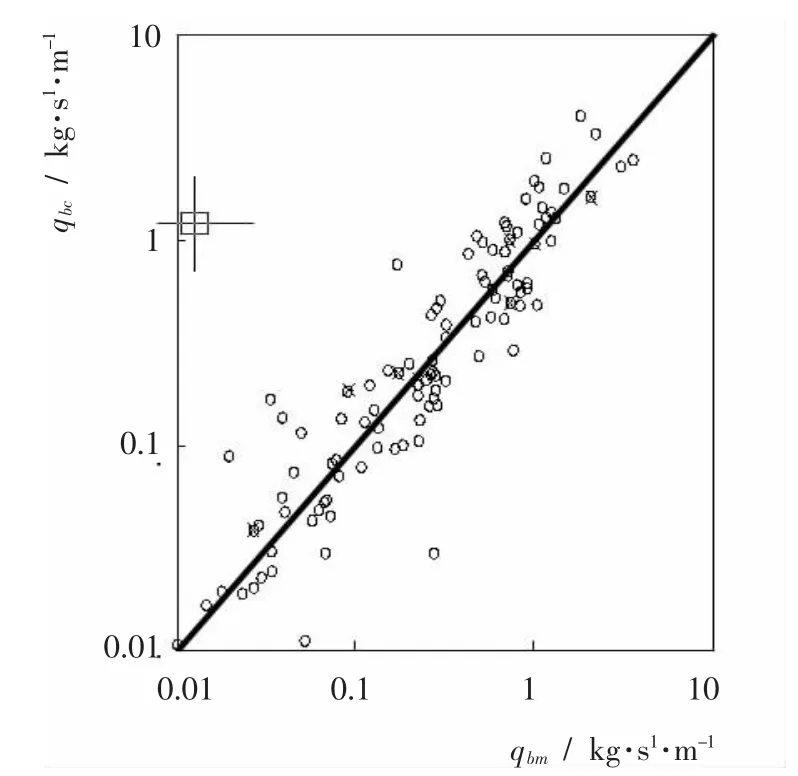
图6 长江下游大通水文站悬移质单宽输沙率计算值与实测值的比较图Fig.6 Comparison of the computational suspended load single-width sediment discharge and measured value of Datong hydrological station of The Yangtze River downstream

上述分析表明， 用本文所建立的单宽推移质输沙率公式用于不同资料的计算时， 除个别点群有一定分散性外， 其计算结果与实验观测结果和实测结果相比有较好一致性， 其计算精度可以满足工程需要。 该公式在分析以推移质为主要运动形式和全沙输沙率方面具有较高的计算精度和应用价值。

3 结语

（1）基于推移质运动滞后于水流运动的特点，根据能量平衡观点和水沙运动的相对关系， 建立了单宽推移质输沙率公式。采用实验资料，对公式参数进行了率定，并对公式进行了验证。

（2）根据实验资料及实测资料，对建立的输沙率公式验证。结果表明，以推移质为主的单宽输沙率公式和全沙单宽输沙率公式计算的结果与水槽实验资料和河道实测资料观测输沙率结果符合度较高。本文公式具有结构简单、 参数较少和计算精度较高等优点，应用价值较高。

[1] Laursen E M. The total sediment load of streams ［J］.Journal of Hydraulics Division， ASCE， 1958， 84（HY1）： 1530－1－36.

[2] Simons D. B. and Richardson， E. V. Forms of bed roughness in alluvial channels ［J］. Journal of the Hydraulics Division， ASCE， 1961， 87（3）： 87－105.

[3] Stein， R. A. Laboratory studies of total load and apparent bed load ［J］. Journal of Geophysical Research，1965， 70（8）： 1831－1842.

[4] Nakato， T. Tests of selected sediment－transport formulas［J］. Journal of Hydraulic Engineering， ASCE， 116（3），1990： 362－379.