时变时滞细胞神经网络的同步研究与仿真

彭战松，张 哲

（黄河水利职业技术学院，河南 开封 475004）

0 引言

细胞神经网络是一种处理实时信息的大规模非线性的模拟电路。 它作为一种动力系统，具有与元细胞自动机类似的并行运算能力。 而在系统的动态特性中，稳定性是至关重要的。 近年来，学术界对神经网络的渐进稳定性和指数稳定性有了广泛的研究［1～5］。然而，模型误差、外部扰动和参数波动将会导致模型不确定性的产生，从而使系统的动态特性变得更加复杂。 所以，系统模型应该具有一定的鲁棒性。 在神经网络的电子线路实现中，由于运算放大器的切换速度有限， 时滞的存在是不可避免的。当时滞的最小值大于零时，时滞就在一个区间范围内变化，这时称为区间时滞。 针对区间时变时滞系统的一些性质，已经有了一部分研究成果［6～9］。 而对具有区间时变时滞的神经网络，指数稳定性的研究还很少。

本文针对一类带有范数有界不确定性的时变时滞神经网络系统，给出了时变时滞依赖的鲁棒渐进稳定和指数稳定性准则， 并通过数值例子仿真，验证了结论的有效性。

1 时变时滞神经网络全局渐进稳定分析

1.1 时变时滞不确定神经网络系统的描述

考虑如下时变时滞不确定神经网络系统：

式中： x(t)=［x1(t)，x2(t)，…，xn(t)］T∈Rn是状态向量；C=diag(c1，c2，…，cn),(ci＞0)是对角正定矩阵；A=(aij)n×n，B=(bij)n×n分 别 代 表 反 馈 和 离 散 连 接 权 矩阵；f(x(t))=［f1(x1(t))，f2(x2(t))，…，fn(xn(t))］是神经元激励函数；J=［J1，J2，…，Jn］是外界常值输入向量；ΔC(t)，ΔA(t)和ΔB(t)是具有如下形式的不确定性。

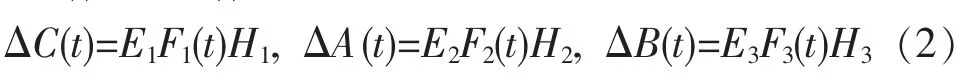
其中，Ei,Hi(i=1,2,3)是已知的具有适当维数的矩阵；Fi(t)(i=1,2,3)是时变不确定矩阵，且满足

时变时滞满足下列条件：

（Ⅱ）τ1≤τ(t)≤τ2和≤μ,τ1,τ2是非负数。

显然，（Ⅰ）比（Ⅱ）更具通用性。 下面将分别根据（Ⅰ）和（Ⅱ）讨论神经网络系统的稳定性准则。

假设神经元激励函数fi(·)(i=1,2,3,…,n)有界且满足如下条件：

式中：l-i, l+i(i=1,2,…,n)是常数。因l-i, l+i(i=1,2,…,n) 可以是正数、 负数和零， 故神经元激励函数比Sigmoid 型激励函数和Lipschitz 型激励函数更弱一些。

由著名的Brouwer’s 固定点理论可知，系统（1）至少存在一个平衡点。 设系统的平衡点为x*=［x*1，x*2，…，x*n］T，通过变换z(·)=x(·)-x*，将平衡点转移到原点，则系统（1）变为：

其中，z(t)=［z1(t)，…，zn(t)］T，g(z(t))=［g1(z1(t))，…，zn(zn(t))］T分别是系统变化的状态向量和激励函数，且gi(zi(t))=fi(zi(t)+x*i)-fi(x*i)。

激励函数gi(·)满足：

故讨论系统（1）平衡点x*的稳定性问题将转化为讨论系统（5）的原点的稳定性问题。

1.2 时变时滞不确定神经网络系统判定

引理1［10］： 设U,V,W,M 是适当维数的实数矩阵，M 满足M=MT，若M+UVW+WTVTUT＜0，则所有的VTV≤I。 当且仅当存在一个正数ε 满足M+ε-1UUT+εWTW＜0。

引理2［11］：（Schur complement） 对给定的矩阵满足S11=ST12，S22=ST22，则下列条件等价：

（1）S＜0；

（2）S22＜0,S11-S12S-122ST12＜0；

（3）S11＜0,S22-ST12S-111S12＜0。

引理3［12］：（S－procedure）设Ti(i=0,1,…，n)是对称矩阵，如果存在标量τi≥0(i=0,1,…，n)使得

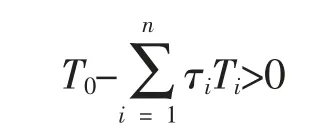
则对任意的Ti＞0(i=0,1,…，n)，有T0＞0.

下面讨论系统（5）的全局鲁棒渐进稳定性准则，时变时滞满足条件（Ⅰ）。

首先，研究下面的标称系统的稳定性。

定理1［13］：设有非线性系统：=A(t)x+O(x,t)对所有的t，有o(O,t)=0。 如果下列条件成立，则式子=A(t)x+O(x,t)的零解是一致、渐近、稳定的。

（2）对于所有的t，A(t)都是有界的；

在上述定理中，条件（1）与条件（2）对参数相同系统是成立的；条件（3）保证了条件Lyapunov 指数全为负。这个定理把通常检验稳定性的方法（Jacobin本征值方法）推广到任意驱动都能用的Lyapunov 指数方法。

记L1=diag(l-1l+1,l-2l+2,…,l-nl+n)，L2=diag(l-1+l+1,l-2+l+2,…,l-n+l+n)，对τ＞0，系统（8）的平衡点是全局渐进稳定的。 如果：

（a）存在正定矩阵P＞0,R＞0,Q1＞0,Q2＞0；

（b）对角矩阵S=diag(s1,s2,…,sn)≥0，M=diag(m1,m2,…,mn)≥0；

（c）和适当维数的矩阵Yi(i=1,2,3)，Ti(i=1,2)满足

其中：Φ11=Q1+Y1+YT1-T1C-CTTT1-2L1S, Φ12=PT1-CTTT2+YT2, Φ22=τR-T2-TT2, Φ33=-(1-μ)Q1-Y3-YT3-2L1M,＊代表矩阵对称位置元素的转置。

证明：对系统（8）构造如下的Lyapunov 函数

其中：V1(t)＝zT(t)Pz(t)，。P,R,Q1和Q2是正定矩阵.

沿系统（8）的轨迹求出Lyapunov 函数V1(t)对时间t 的导数，可以得到

由Leibniz－Newton 公式

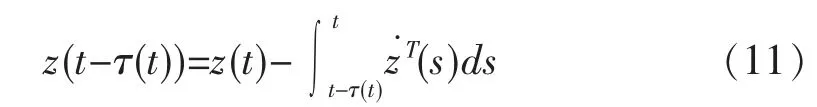
得，存在适当维数的矩阵Yi(i=1,2,3)满足：

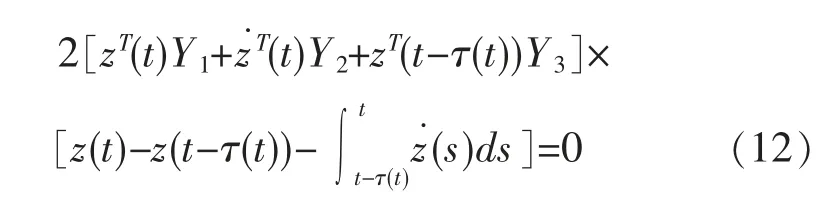
考虑系统中矩阵的关系， 存在适当维数的矩阵Yi(i=1,2,3)满足

由引理3 得，若存在实数对角矩阵，S=diag(s1,s2,…,sn)≥0 和M=diag(m1,m2,…,mn)≥0 满足

应用引理2，由式（9）可得Ξ(t)＜0，从而有V˙1(t)＜0 成立。根据Lyapunov 稳定性理论（定理1）可知，系统（8）是全局渐进稳定的。

2 实例分析与仿真

2.1 时变时滞的超混沌Rössler 系统的描述

为了研究问题的方便， 取时变时滞的超混沌Rössler 系统为研究对象。

超混沌Rössler 系统［12］可描述如下：

其中，x,y,z,w 为系统的状态向量， 当系统参数a=0.25,b=3.0,c=0.05,d=0.5 时， 系统处于超混沌状态。通过数值仿真得到超混沌系统的Lyapunov 指数图（如图1 所示）以及超混沌吸引子（如图2 所示）。

图1 超混沌Rössle 系统的Lyapunov 指数图Fig.1 Lyapunov index of the Hyperchaos Rössle system

图2 超混沌Rössler 系统相图Fig.2 Phase diagram of Hyperchaos Rössle system

图1中，4 条线分别代表系统（15）的Lyapunov 指数情况。 图2 为系统（15）的混沌吸引子。

2.2 数值仿真实验

时变时滞超混沌Rössler 系统变换可描述如下：

其中，x,y,z,w 为系统的状态向量，τ(t)为时变向量。 若系统参数a=0.25,b=3.0,c=0.05,d=0.5，系统处于超混沌状态。 取

图3 误差曲线Fig.3 Error curve

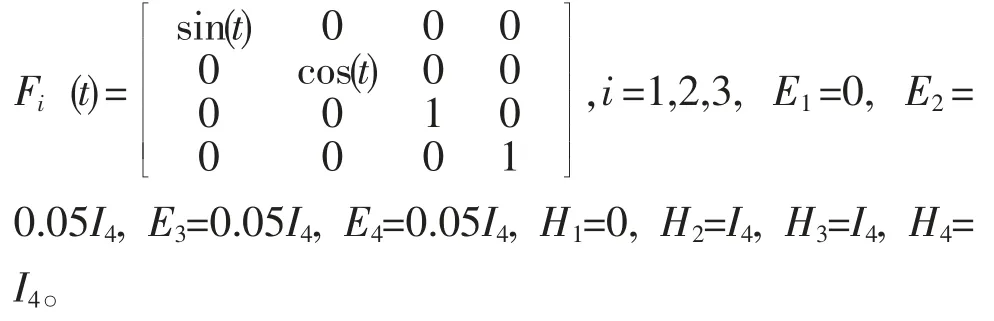
从图3 中的e1,e2,e3,e4,四条误差线可以看出，时变时滞细胞神经网络变化同步，随着时间的增加，误差曲线逐渐趋于零，系统趋于稳定状态。

3 结语

综上所述，本文通过Lyapunov 稳定性定理和线性矩阵不等式技术， 得到一个新的与时滞相关的稳定性条件。 并通过一个数值例子来验证所得定理的有效性。 同时，该方法也可用于随机神经网络、脉冲神经网络等的研究。

［1］ H.B.Zhang，C.G.Li，X.F.Liao.A Note on the Robust Stability of Neural Networks with Time Delay.Chaos，Solitions and Fractals，2005，25（2）：357－360.

［2］ J.H.Zhang，J.Q.Qiu，P.Shi.New Robust Stability Criteria for Uncertain Neural Networks with Time －Varying Delays.First international conference on innovative computing information and control，2006，（3）：648－651.

［3］ H.Yang，T.Chu，C.Zhang.Exponential Stability of Neural Networks with Variable Delays via LMI Approach.Chaos，Solitons and Fractals，2006，30（1）：133－139.

［4］ Y.He，M.Wu，J.H.She.An Improved Global Asymptotic Stability Criterion for Delayed Cellular Neural Networks.IEEE Trans.Neural Networks，2006，17 （1）：250－252.

［5］ Y.He，Q.G.Wang，W.X.Zheng.Global Robust Stability for Delayed Neural Network swith Polytopic Type Uncertainties.Chaos，Solitons and Fractals，2005，26 （5）：349－1354.

［6］ K.W Yu，C.H.Lien.Stability Criteria for Uncertain Neutral Systems with Interval Time －varying Delays.Chaos，Solitons and Fractals.doi：10.1016／j.chaos.2007.01.002.

［7］ X.F.Jiang，Q.L.Han.Delay－dependent Robust Stability for Uncertain Linear Systems with Interval Time－varying Delay.Automatica，2006，42（6）：1059－1065.

［8］ X.F.Jiang，Q.L.Han，X.H.Yu.Stability Criteria for Linear Discrete－time Systems with Interval－like Time－varying Delay.2005 American control conference，2005，（8－10）：2817－2822.

［9］ X.F.Jiang，Q.L.Han.On Control for Linear Systems with Interval Time－varying Delay.Automatica，2005，41（12）：2099－2106.

［10］ V.Singh.Robust Stability of Cellular Neural Networks with Delay：Linear Matrix Inequality Approach.IEEE Proc.－Control Theory Appl，2004，151（1）：125－129.

［11］ B.Boyd， L.E.Ghaoui， E.Feron， V.Balakrishnan. Linear matrix inequalities in systems and control theory.Philadelphia：SIAM，1994：7－36.

［12］ O.E.Rossler. An equation for continuous chaos. Pbys.Lett.A. 1976， 57：397－398.

［13］ 马知恩.常微分方程定性与稳定性方法［M］.西安：科学出版社，2001：70－71.