圆锥凸度滚子轴承的接触特性研究

2013-12-09张建忠沈艳河李自鹏

黄河水利职业技术学院学报 2013年4期

张建忠，沈艳河，李自鹏

（1.黄河水利职业技术学院，河南开封 475004；2.黄河水利职业技术学院中小型自动化机械装备工程研究中心，河南开封 475004）

0 引言

利用滚子凸度修形设计，显著改善滚子受力结构，提高承载力与精度稳定性，延长寿命，是滚子研究与技术发展的主线。对数轮廓是圆柱滚子和圆锥滚子提高轴承寿命的关键［1］。圆锥滚子轴承的接触曲率不恒定特性直接决定轴承性能，罗继伟等［2～4］使用切片方法研究了圆锥滚子轴承中的接触应力分布；Diaconescu［5］使用多项式曲线对圆锥滚子母线进行修正，以期改善接触压力分布状态；杨萍等［6～7］分析了圆锥滚子的弹性流体动力润滑（EHL）特性。

圆锥滚子轴承的滚子与内／外滚道之间的接触在局部上与圆柱滚子相似。但其存在接触曲率沿接触线方向改变、接触弹性变形量沿接触线产生不一致情况，即接触面沿接触线呈现不对称分布，和接触区超高压力一起，造成应力分布不均匀，即偏载效应。圆锥滚子从非接触区到接触区的过程中，起始受力状态关系到滚子的接触承载力和动态特性。如果圆锥滚子的受力分布与它的凸度中心不能重合，则需要保持架对其局部施加力，才能维持力学平衡，但这种状态是不稳定的。本文试从接触应力分布和偏载效应分析出发，分析圆锥滚子轴承的接触特性。

1 凸度滚子接触应力的计算条件与方法

1.1 计算条件

1）弹性半空间假设。将滚子与内／外滚道接触看作一个弹性和曲率相当的物体与一刚性平面的接触。

2）Herz 接触假设。包括不考虑摩擦力、接触点预先确定、小变形等。 Herz 接触是很强的假设，但由于轴承中弹性动力润滑油膜的存在，在工程计算中的误差可忽略不计。

1.2 计算方法

根据以上假设，可沿接触线方向建立坐标系： x为接触线方向；y 为接触面上通过接触线中点且垂直于接触线方向，也即接触宽度方向；z 为通过原点并垂直于接触面的轴线。圆锥滚子的接触一般采用点接触问题的解（即Herz 接触的Boussinesq 解）通过积分解得。即

式中：Q 为总接触力；p(x,y)为接触力分布；s 为接触区；E′为当量弹性模量，，v1、v2为接触物体的泊松比，E1、E2为接触物体的弹性模量；x′y′为坐标系中接触区内的点；δ 为弹性趋近量；z 为原始距离。

离散化方程（1）和（2），得到：

式中：aj、bj分别为接触线方向上和接触宽度方向矩形单元长度的1／2，j 为单元序号（下同）；Pj为单元上的接触压力；D 为柔度矩阵。

此外，还应满足接触区压力非负条件。将式（4）无量纲化：

其中：a 为沿接触线方向的单元长度，接触宽度方向单元的长度可设为a 的分数，如1／10 a。同样，接触弹性趋近量和原始距离也可使用a 的倍数表示。使用无量纲化参数可反映接触系统中各参数的数量关系，且方便程序编写。

研究区域分为单元格子，沿接触线方向按200份分割，宽度方向50 份，单元宽度按0.1 计算。采用假设条件和式（3）～（6）建立方程，得到200×50 个方程组。根据弹性趋近量假设计算各单元的接触压力，并根据接触区压力和弹性趋近与原始距离之差非负假设调整方程组结构。化弹性接触问题为正定系数矩阵的线性方程组问题，使用共轭梯度法反复迭代计算，直到计算无量纲接触压力值与上次计算误差不超过10-7，得到压力分布结果，作为进一步计算和分析的基础。

为方便计算，用假设弹性趋近量方法，分析在理想弹性趋近情况下，接触力和滚子从非载荷区至载荷区域的运行姿态变化情况，得到圆锥凸度滚子的接触特性。

2 接触应力的计算结果和分析

2.1 无凸度接触应力计算

考虑圆锥滚子在内外圈滚道的接触，圆锥滚子接触当量锥角设为15°，无量纲计算接触线长度200格。其中含两端圆角10 格，宽度方向5 格，小端当量接触曲率半径150 格。沿接触面垂直方向施加弹性趋近量0.05 格，使用Matlab 数学分析软件计算无量纲接触压力分布。无凸度接触下的压力分布计算结果如图1 所示。

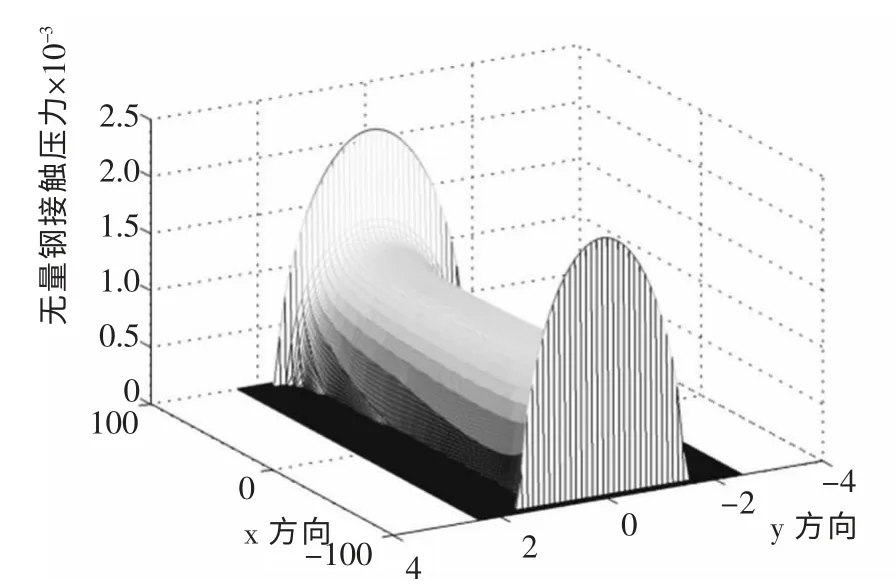
图1 无凸度滚子接触压力分布Fig.1 Non-convexity roller contact stress distribution

由图1 可以看出，沿接触线方向呈现两端高中间平稳的状态。这是由于滚子端部圆角远小于接触曲率半径，在边缘处接触应力出现陡坡上升。在滚子边缘处的接触应力奇大，其数值与端部的圆角过渡光滑性密切相关，如圆弧过渡存在尖角，则会出现较高的边缘应力。由图中的斜向跌落纹路分布可知，圆锥滚子大端接触应力大于小端接触应力。在这种情况下，确定接触性能的主导问题为边缘效应。

2.2 对数凸度接触应力计算

为减少上述边缘效应，通常采用修正滚子边缘处母线轮廓形状的方法，使接触应力符合无限长假设的状态，从而达到减少边缘应力集中，增加寿命优化设计的目的。关于这方面的研究，先后出现了修正线、圆弧和Lundberg 对数等曲线轮廓修正滚子形状。其中，对数曲线轮廓能够使应力状态符合无限长假设，为最优设计。工程上已经成功地将其应用于轴承制造领域，如瑞典SKF 公司的Explore 系列对数母线滚子轴承、德国Schaeffler（FAG 和INA）对数滚子轴承、美国RBC 轴承公司的Tyson 型圆锥对数滚子轴承、日本NTN 和Koyo 轴承公司的优化对数曲线凸度滚子轴承等。在均匀接触曲率条件下，对数方程为：

式中：z 为接触中心线初始距离；Q 为接触承载力，即设计载荷，可采用无凸度计算结果作为计算值；L 为接触线长度；x 为滚子边缘至接触线中点的距离。

由公式（7）得到的轮廓曲线为沿接触线中心对称的廓形，在圆柱滚子轴承中已经广泛应用，可普遍延长轴承寿命3 倍以上（SKF）。

不改变其他计算条件，轮廓形状采用公式（7）对

图2 圆锥对数凸度滚子压力分布Fig.2 Stress distribution of circular cone to convexity roller

数曲线，按前述方法计算接触应力分布，结果如图2所示。

从图2 可以看出，对数圆锥凸度滚子有效减少了边缘处的应力奇异现象，即边缘处压力逐步减少为0，接触压力在接触线方向分配基本均匀，最大值较无凸度圆锥滚子减少近一倍。

2.3 偏载效应计算

上图中，x 正值方向为圆锥滚子大端，y 方向为接触宽度方向。考察图2 中接触压力的精细分布，分析接触应力纹路可得：在接触压力图中，尽管最大应力的差异表现不明显，但压力分布的脊纹偏向说明，大端接触压力较凸度中心对称的小端有所增高。据此可推测，压力引起的对数滚子凸度中心（接触线中心和接触坐标原点）的无量纲力矩并不对称，引起滚子向y 轴转动。这种沿凸度中心的倾翻力矩可称为偏载力矩。

其他条件不变，以垂直于接触区的弹性趋近量0.001～0.09 为自变量，通过前述计算方法，计算各弹性趋近条件下的无量纲总承载力Q 和通过接触线中心沿y 轴转动的总无量纲力矩，可得到如图3 的计算结果。

图3（a）所示为弹性趋近量与无量纲载荷之间的关系。在中心对称凸度滚子条件下，载荷随弹性趋近量增加而逐步升高，除弹性趋近量较低时外，基本上呈线性增加趋势。此过程可看作在理想弹性变形情况下，圆锥滚子从非接触区到接触区运动过程中的承载力变化情况。

图3 弹性趋近量与载荷和偏载力矩关系Fig.3 Relations of elastic approach with loading and unbalance loading moment

以凸度顶点（接触线中点）为力矩中心，接触压力产生的偏载力矩与弹性趋近量的关系如图3（b）所示。图3（b）显示，随弹性趋近量的增大，偏载力矩扭转方向的趋势不变，且单调上升，数值上呈现近似二次曲线变化。这说明滚子在从非接触区至接触区逐渐承担载荷的过程中，受到使滚子倾翻于大端并逐渐增大的力矩。

另一方面，考虑滚子受到的偏载力矩发生于滚子／内圈滚道和滚子／外圈滚道，二者之间的不同之处在于合成的当量接触曲率发生改变，不失一般性，可使用不同的合成当量锥角作为自变量，模拟不同接触曲率变化情况下的偏载力矩。假设弹性趋近量为0.05，其他条件不发生改变，当量锥角与无量纲力矩关系如图4 所示。

由图4 可以看出，随着锥角在4°～20°范围内变化，无量纲力矩与当量锥角呈类似线性关系。这说明，只要当量锥角不同，它们的力矩就不能互相抵消而获得平衡状态。

2.4 计算结果分析

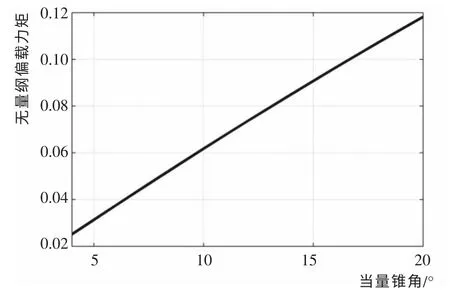
图4 当量锥角与无量纲偏载力矩关系图Fig.4 Relations of equivalent taper angle and dimensionless unbalance loading moment

在滚子理想运动状态下，考虑滚子与内外滚道接触线形成的平面受力情况，平面力矩不能完全消除。显然，这种情况不可能发生。在滚子进入接触区且接触压力上升的过程中，为平衡偏载力矩，滚子会产生一个沿y 轴转动的微小角度，使得接触受力平衡。值得注意，这是一个正反馈过程，即在进入轴承压力区时一定会发生，且偏斜会越来越大，或在端部局部应力越来越高，由此产生了滚子在径向平面内的歪斜现象，造成圆锥滚子轴承的早期失效。

在上述受力条件下，可能产生下述情况：倾翻力矩影响摩擦力分布，在受到接触力矩较大时，使得保持架在确定区域受力、在保持架限定的自由度范围内产生偏摆现象。