分离变量法在数学物理方程中的应用
2013-12-08智丽丽李艳青
智丽丽 李艳青
(1,2.昌吉学院物理系 新疆 昌吉 831100)
1 分离变量法的概述
分离变量法关键是把分离变数形式的试探解代入偏微分方程,从而把它分解为几个常微分方程,问题转化为求解常微分方程[1-6]。另一方面,代入齐次边界条件把它转化为常微分方程的附加条件,这些条件与相应的常微分方程构成本征值问题。虽然我们是从驻波引出解题的线索,其实整个求解过程跟驻波并没有特殊的关系,从数学上讲,完全可以推广应用于线性齐次方程和线性齐次边界条件的多种定解问题。这个方法,按照它的特点,叫做分离变量法。
2 分离变量法求解方程的应用
2.1 第一类边界条件定解问题的求解
研究两端固定的均匀弦的自由振动,即定解问题
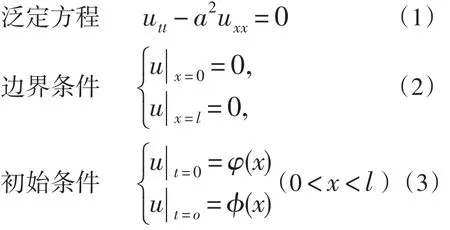
这里研究的弦是有限长的,它有两个端点,波就在这两端点之间往复反射,两列反向行进的同频率的波形成驻波。这就是启发我们尝试从驻波出发解决问题。这样,驻波的一般表示为
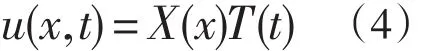
在这里自变数x只出现于X之中,自变数t只出现于T之中,驻波的一般表示式具有分离变数的形式。
那么,在两端固定的弦上究竟有哪些驻波呢?把驻波的一般表示式(4)代入弦振动方程(1)和边界条件(2),得
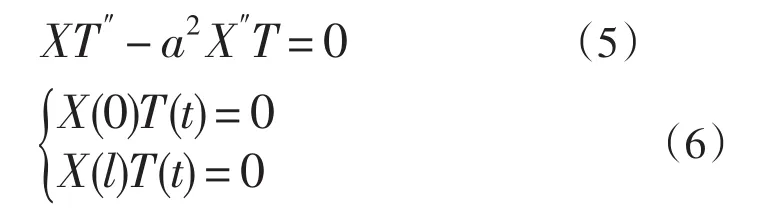
条件(6)的意义很清楚:不论在什么时刻t,X(0)T(t)和X(l)T(t)总是零。这只能是

注意:由于边界条件是齐次的,才得出(7)这样简单的结论,现在再看方程(5),用a2XT遍除各项即得。左边是时间t的函数,跟坐标x无关;右边则是坐标x的函数,跟时间t无关。两边相等显然是不可能的,除非两边实际上是同一个常数。把这个常数记作-,这可以分离为关于X的常微分方程和关于T的常微分方程,前者还附带有条件(7),
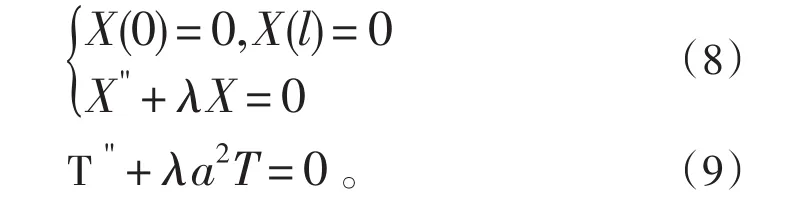
先求解X,将λ<0,λ=0,λ>0三种可能性逐一加考察。
②λ=0,方程(8)的解是X(x)=C1x+C2积分常数C1和C2由条件(1.7)确定,即,由此解出C1=0,C2=0,从而X(x)≡0,所求驻波u=XT≡0,没有意义。于是,λ=0的可能性也排除了。
③λ>0,方程(8)的解是X(x)=C1cos+C2Sin,积分常数C1和C2由条件(7)确定,即,如Sin≠0,则仍然解出从而u(x,t)≡0,同样没有意义,应序排除。现只剩下一种可能性:于是,(n为正整数),即
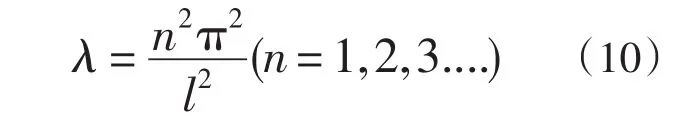
当λ取这样的数值时,
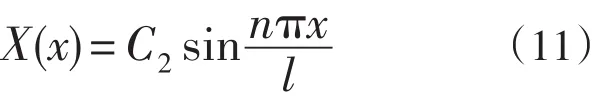
C2为任意常数。请注意,(11)正是博里叶正玄级数的基本函数族。这样,分离变数过程中引入的常数λ不能负数或零,甚至也不能是任意的正数,它必须取(10)所给出的特定数值,才可能从方程(8)和条件(7)求出有意义的解。常数λ的这种特定数值叫作本征值,相应的解叫作本征函数。方程(8)和条件(7)则构成所谓本征值问题。
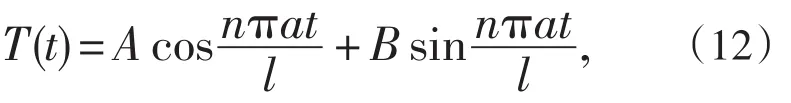
其中A和B积分常数,把(11)和(12)代入(4),得到分离变数形式的解
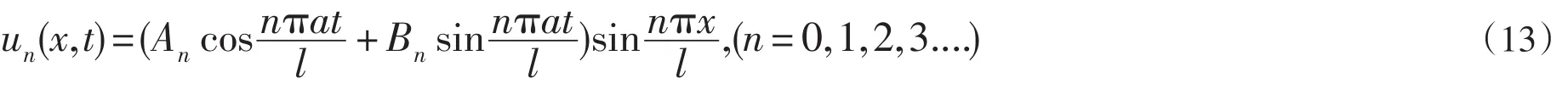
n为正整数,这就是两端固定弦上的可能的驻波。每一个n对应于一种驻波,这些驻波也叫作两端固定弦的本征振动,在x=κl n(κ=0,1,2,....n)共计n+1点上,sin(nπx l)=sinκπ=0,从而un(x,t)=0。这些点就是驻波的节点,相令节点间隔l n应为半波长,所以波长=2l n。
本征振动(13)的角频率(又叫圆频率)是ω=nπa l,从而频率 f=ω 2π=na 2l。n=1的驻波除两端x=0和x=l外没有其它节点,它的波长2 l在所有本征振动中是最长的,相应地,它的频率a 2l在所有本征振动中最低的。这个驻波叫作基波。n>1的各个驻波分别叫作n次谐波。n次谐波的波长2l n是基波的1 n,频率na 2l则是基波的n倍。
以上本征振动是满足弦振动方程(1)和边界条件(2)的线性独立的特解。由于方程(1)和边界条件(2)都是线性而且齐次的,本征振动的线性叠加
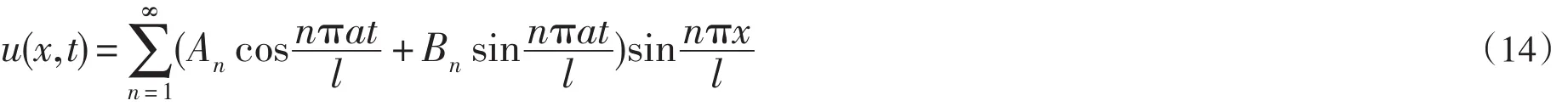
仍然满足方程(1)和边界条件(2),这就是满足方程(1)和边界条件(2)的一般解,其中 An和Bn为任意常数。这里尚未考虑初始条件。
下面的任务便是求定解问题(1)∽(3)的确定解,在数学上,就是要选取适当的叠加系数An和Bn使(14)满足初始条件(3)。为此,以(14)代入(3),

(15)的左边是傅里叶正弦级数,这就提示我们把右边的ϕ(x)和φ(x)展开为傅里叶正弦级数,然后比较两边的系数就可以确定An和Bn,

至此,定解问题(1)∽(3)已经解出,答案是(14),其中系数An和Bn取决于弦的初始状态,具体计算公式是(16)。解(14)正好是傅里叶正弦级数,这是在x=0和x=l处的第一类齐次边界条件(2)所决定的。
2.2 第二类边界条件定解问题的求解
前面已研究了区间两端均为第一类齐次边界条件的定解问题,下面例是区间两端均为第二类齐次边界条件的例题。即定解问题
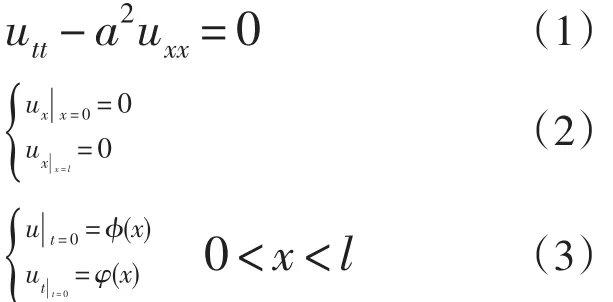
解 按照分离变量法的步骤,先也分离变量形式的试探解
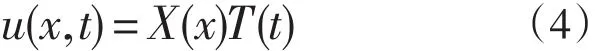
代入泛定方程(1)和边界条件(2),得
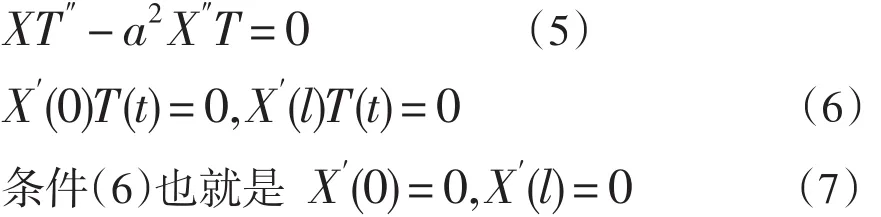
再看方程(5),用a2XT遍出各项即得,两边分别是时间t和坐标x的函数,不可能相等,除非两边实际上是同一个常数。把这个常数记作-λ,,这可分离变为关于X的常微分方程和关于T的常微分方程,前者附带有条件(7),即有:

求解本征值问题(8),(7)。如果λ<0,只能得到无意义的解X(x)≡0。如果λ=0,则方程(7)的解是,代入条件(7),得D0=0,于是为任意常数,这是对应于本征值λ=0的本征函数。如果λ>0,方程(8)的解是:,积分常数C1和C2由条件(7)确定,即
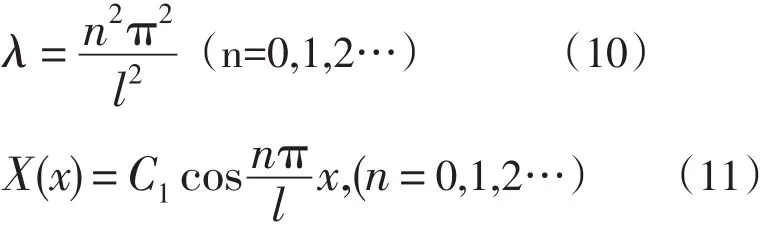
C1为任意常数。(11)即傅里叶余弦的基本函数族。
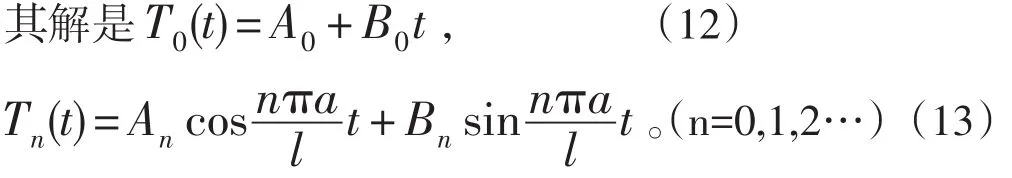
其中 A0,B0,An,Bn均为独立的任意常数,把(11),(12)和(13)代回(4),得到本征振动
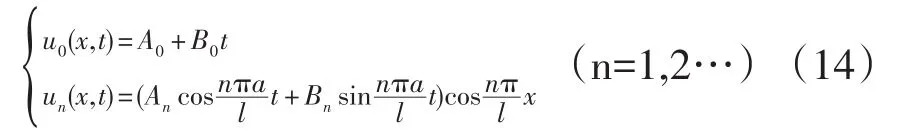
请注意,(14)正是傅里叶余弦级数的基本函数族。所有本征振动的叠加应是一般解u(x,t),即
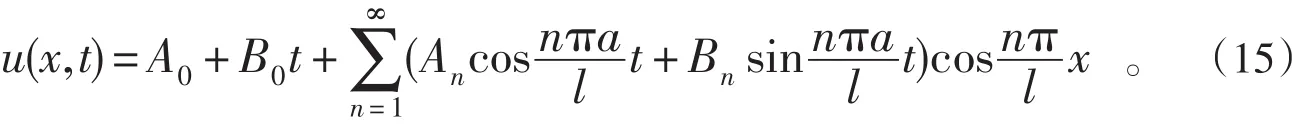
系数 A0,B0,An,Bn应由初始条件(3)确定,以(15)代入(3),有
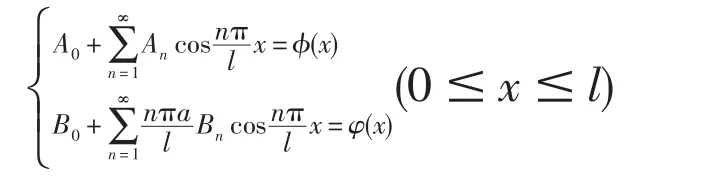
把右边的ϕ(x)和φ(x)展开为傅里叶余弦级数,然后比较两边的系数,得
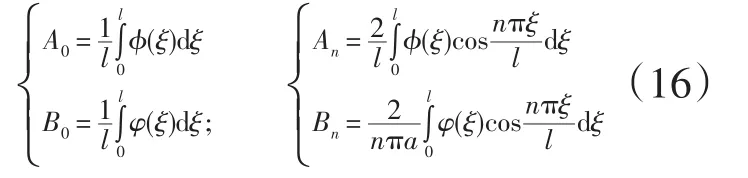
(15)中的A0+B0t描写杆的整体移动,其余部分才真正描写杆的纵振动,从(16)知道A0与B0分别等于平均初始位移和平均初始速度,由于不受外力作用,杆以不变的速度B0移动,解(15)正是傅里叶余弦级数,这是在x=0和x=l处的第二类齐次边界条件(2)决定的。
3 结论
本文通过两种不同边界条件下振动方程的求解,不难看出,分离变量法的基本思想是把多元函数所满足的偏微分方程转化为若干个一元函数的常微分方程,主要是产生本征值方程,再借助已有的数学知识得到相应方程的解。
[1]吴少平.数学物理方程的几种解法[J].高等函授学报,1999,(1):22-24.
[2]谢焕田.分离变量法的应用[J].高师理科学报,2010,30(3):4-5.
[3]张健.数学物理方程的分离变量法[J].青海师范大学学报,2011,(3):17-19.
[4]梁昆淼.数学物理方法[M].高等教育出版社,2010.
[5]黄大奎,舒慕增.数学物理方法[M].高等教育出版社,2001.
