BD2无源授时原理分析与测试*

翟昆朋 ，何文涛 ，2，徐建华 ，2，叶甜春

（1.中国科学院微电子研究所，北京 100029；2.杭州中科微电子有限公司，浙江 杭州 310053）

全球卫星导航系统（GNSS）已经成为授时的最主要工具之一，在时钟驯服、无线通信系统、电力系统等领域得到广泛应用[1-3]。随着第二代北斗系统区域组网的完成，目前的在轨卫星有 5颗地球静止轨道（GEO）卫星、4颗中圆地球轨道（MEO）卫星和5颗倾斜地球同步轨道（IGSO）卫星，初步形成了覆盖亚太地区的定位、授时服务能力[4]。

1 实现原理

下面将从基本测量值（伪距）出发说明GPS授时原理。如图1所示，卫星信号发射时间为ti的发射信号在tu时刻被接收机收到，该卫星对应的伪距测量值为ρi。估计出接收机时间与GPS时间的差别δtu=tu-tGPS，即实现了本地时间和GPS系统时间的同步。

将伪距表示为用户与卫星的距离r、电离层延迟I、对流层延迟T、卫星和接收机时钟误差等组合的形式：

2 授时精度分析

卫星接收机得到的伪距测量值有许多误差源，这些误差的统计特性直接影响测量值精度，进一步影响接收机定位授时的精度。本节以GPS系统为例，分析卫星接收机授时精度。

在非静止或者位置未知的情况下，接收机定位和授时同时进行，位置和时间解的精度可以表示为几何精度因子和伪距误差因子之积[5-6]，即：

位置时间误差=几何精度因子×伪距误差因子 (2)

在一定条件下，伪距误差因子为用户等效距离误差（UERE）。典型的单频C/A码接收机的 UERE预算[6]如表1所示。

表1 GPS标准定位服务的典型UERE预算

而几何精度因子 (DOP)与卫星和用户的几何分布相关。以GPS时间2013年1月7日7时26分的位置[120.156 3 E，30.186 1 N，100 m]所有仰角大于 5°的 GPS卫星几何分布为例。当时当地可见卫星共11颗，时间精度因子为TDOP=1.1，三维位置精度因子为PDOP=0.9。假设各个卫星测量噪声不相关，利用表1中列出的用户等效距离误差（UERE）数据，计算出时间偏差误差为：

基于以上假设，时间估计的误差约为2.6 ns。因为各个卫星之间误差相关性很强，所以利用DOP×UERE计算得到的误差往往大于实际计算出的误差。目前大部分商用接收机的授时精度都优于该数值，达到10 ns～20 ns(1σ)水平。

3 1PPS信号的生成

卫星接收机的授时形式是输出与UTC(或卫星系统时)整数秒时刻同步的秒脉冲1PPS(One Pulse Per Second)，如图2所示。

接收机在每一个测量历元实现位置和时间差估计后，可以确定该历元采样时刻对应的系统时间tuGPS=tu-δtu，另外还可以计算出晶振频率偏差 δf。 假如 tuGPS离下一个整数秒时刻tNextSec的时间间隔为△T，用于1PPS信号产生的本地参考时钟标称频率为fref，估计得到的频率偏差为δf，则下一个1PPS脉冲需要在采样时刻后第 N=「fref(1+δf)△T个参考时钟上升沿输出，其中「为向上取整符号。1PPS信号产生时间关系如图3所示。

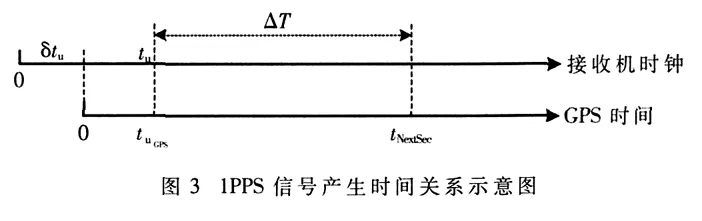
由于本地参考时钟频率受限，输出过程有取整处理，所以1PPS的输出有一定的颗粒度，即实际输出的1PPS信号对应的时间有一个系统误差 δtpps=△T-Nfref(1+δf)，误差最大值幅度与参考时钟频率成反比±1/(2f)。所以在第n个历元，接收机输出的1PPS时间误差是两个部分的叠加，即：

式中，v(n)、w(n)分别为本地时间差估计的误差和时间间隔量化误差。由于本振时钟频率偏差的漂移和本地时间差估计误差的波动，1PPS的误差呈现出类似锯齿波形状的波动。输出1PPS所用的本地参考时钟频率过低会引入大的时间分辨粒度，然而高的时钟频率会导致电路设计复杂度和功耗的增加。接收机的设计需要在直接授时精度与芯片设计复杂度之间进行权衡。

4 测试结果

采用安装于楼顶的多模卫星接收天线，对BD2接收机和支持GPS的LEA-5T接收机的1PPS信号时间间隔进行测试，监测的时间间隔计数保存至个人电脑上进行数据分析。测试平台的示意图如图4所示。

时间间隔计数器利用FPGA搭建，利用单独的50 MHz本地时钟倍频至fcnt=400 MHz作为计数时钟，对1PPS上升沿之间的时间进行计数。这里时间间隔计数同样会因为计数时钟晶振的频偏而引起计数误差，通过对序列进行均值化处理查看其波动，图5为2 h测试过程中记录的BD2接收机时间间隔序列零均值化后的序列。

计算得到该时间间隔序列的标准差为3.73 ns。由图5可见，因为 1PPS的参考时钟 fref≈100 MHz，所以时间间隔误差大部分在-5 ns～5 ns之间波动，少量的波动幅度超过该范围。

因为计数时钟频段导致时间间隔测量值不准确，故对BD2接收机和u-blox接收机的时间间隔序列计数进行差分，分析其统计特性：

式中，M1(n)、M2(n)分别为 BD2和 GPS接收机在第 n秒的时间间隔计数；δfcnt与前面定义类似，不过是未知的，在1 ppm或更小量级；q(n)为两个时间间隔先取整与先做减法两种操作之间的不同而引入的计数差异，取值为(1，0，-1)中的一个。可以看到，d M(n)序列相当于利用 fref对两个接收机时间间隔误差TIE(Time Interval Error)的叠加进行量化，然后再叠加一个额外的误差参数。图6显示该序列对应的时间参量。

该序列的均值为-0.052 ns，标准差为6.333 ns。由此可见，两个接收机输出的1PPS信号在1 s左右的周期时间序列具有高度的一致性。该序列的柱状图如图7所示。

以目前的测试条件还无法测试BD2系统1PPS信号的绝对授时精度，但是其1PPS周期误差的方差和标准差一定小于差分序列的相应统计量。由图7也可以看出，误差差分序列以均值为中心具有很好的对称分布特性。

本文分析了单向卫星授时原理，从卫星系统各个误差源出发分析了理想的无源授时精度。基于自主开发的多模导航基带和射频芯片实现其授时功能，但是受限于1PPS信号产生电路的参考时钟的频率，产生的1PPS信号会有锯齿波状的相位噪声。测试结果显示，在本文所示的测试条件下，单BD2系统的无源授时精度优于 10 ns(1σ)。

[1]单晓庆，杨俊.北斗/GPS双模授时及其在 CDMA系统的应用[J].测试技术学报，2011，25(3)：223-228.

[2]李建，谢小荣，韩英铎，等.北斗卫星导航系统与GPS互备授时的分布式相量测量单元[J].电网技术，2005，29(9)：1-4，9.

[3]倪媛媛，胡永辉，何在民.北斗卫星校准铷钟单元的设计与实现[C].广州：第三届中国卫星导航学术年会-S04原子钟技术与视频系统，2012.

[4]中国卫星导航系统管理办公室.北斗卫星导航系统空间信号接口控制文件公开服务信号B1I(1.0版)[Z].2012.

[5]谢钢.GPS原理与接收机设计[M].北京：电子工业出版社，2009.

[6]KAPLAN E D，HEGARTY C J.GPS原理与应用：Understanding GPS principles and applications[M].寇艳红，译.第二版.北京：电子工业出版社，2006.