基于数字信号处理技术的地磁日变数据处理方法研究
2013-12-06龙生海邹时林王胜平
龙生海,邹时林,王胜平
(东华理工大学 测绘工程学院,江西 南昌 330013)
地磁是地球的一个重要的地球物理特征。地磁场不是恒定不变的,而是随时间缓慢变化的。研究这种变化的时空分布规律对于了解地球内部物质的性质和运动具有重要意义。近年来地磁在水下无源导航以及地震预报方面的研究也取得了突破性的进展[1-3],已经成为地震监测的重要手段。地磁台站是最基本的地磁监测手段。我国的地磁台网发展迅速,1Hz采样率的数据已经成为现实[4-5]。如何对如此高密度的地磁时间序列数据进行快速准确的分析计算成为研究的重点,包含准确变化特征的地磁日变数据是地震科学研究的根本保障。
正是基于此背景,本文提出基于数字信号处理技术的地磁日变处理技术,并对整个数据处理过程进行深入分析。
1 理论方法
傅里叶变化是数字信号处理技术中最经典的算法,对于离散的地磁观测序列,离散傅里叶变换实现了频域离散化,在数字信号处理技术中起着及其重要的作用,它可以直接用来分析信号的频谱、计算滤波器频率响应,以及实现信号通过线性系统的卷积运算等。该方法既可以大大减少运算时间,在选取合适的截止频率的情况下又可以实现有用信息的最大保留。
傅里叶变化可以看做是傅里叶级数的连续形式。傅里叶级数把定义在[-π,π]上的信号分解为频率为整数倍关系的谐波分量组合,相应的傅里叶变换将一个无限时宽的信号分解为频率为λ的一系列频率分量,其中λ可以是任意实数(甚至是复数)。如果x(t)是定义在整个实轴上的实值或复值函数,则其傅里叶变换可由式(1)给出。
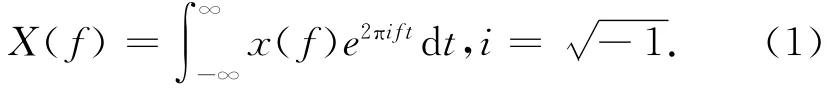
若对任意参数f,上述积分都存在,则式(1)确定了一个函数X(f),称为X(f)的傅里叶变换,如果已知X(f),则利用如下的傅里叶逆变换,还可以复原x(t)。
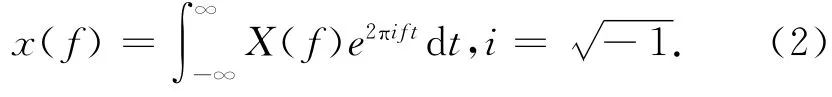
若x(t)和X(f)同时满足式(1)和式(2),则称它们是一个傅里叶变换对,记为x(t)↔X(f),通常X(f)是一个复函数,因此可以写成以下2部分:
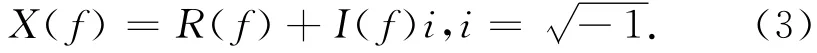
式中:R(f)和I(f)分别是X(f)的实部和虚部。将式(3)表示成指数形式常常是方便的。

快速傅氏变换(FFT),是离散傅氏变换的快速算法,它是根据离散傅氏变换的奇、偶、虚、实等特性,对离散傅里叶变换的算法进行改进获得的。它对傅氏变换的理论并没有新的发现,但是对于在计算机系统或者说数字系统中应用离散傅里叶变换是很大进步。
该算法可以实现离散信号从时间域到频率域的转换,在得到信号的频率之后,可以根据实际需要删除或保留自己需要的频率段,将所保留的数据再进行傅里叶逆变换。最终实现对离散地磁数据的平滑处理。
2 处理过程
2.1 质量控制
各类地磁变化具有不同的相态和时空分布特征,并且常常叠加在一起,起伏变化有时比较平缓,有时比较剧烈。有时就形成了一种复杂的干扰。同时地磁数据对外界的干扰十分的敏感。如果测站周围有任何磁性体都会对原始地磁数据序列产生很大的干扰,从而引起地磁数据的异常突变。因此在数据处理之前必须首先对原始观测数据进行相应的质量控制[6-8]。
本文所述方法采用抗差卡尔曼滤波与人工交互式方法相结合的办法实现了对地磁日变数据的质量控制。
2.2 基于FFT的地磁数据平滑方法研究
目前地磁数据的采样率已经可以到达1Hz的频率。如此高采样率的地磁数据虽然可以更好反应地磁变化,但是由于各种原因引起的小的噪声,使数据呈现一种锯齿状的变化特征。具有不同时变特征的数据有不同的用处,因此研究可以方便为不同用户快速提供不同特征数据的方法显得至关重要。本文基于第一部分提出的FFT数字信号处理技术,展开对地磁日变数据的平滑处理。
地磁日变数据的平滑处理一直是地磁数据处理中一个重要的环节。利用FFT算法可以将地磁日变观测数据从时间域转换到频率域,再根据相应的截止提取地磁日变序列中的长周期信号,最后将提取出的信号通过FFT逆变换转换到时间域。该方法也可以实现地磁数据的平滑。但是其中截止周期的确定是至关重要的一个环节。
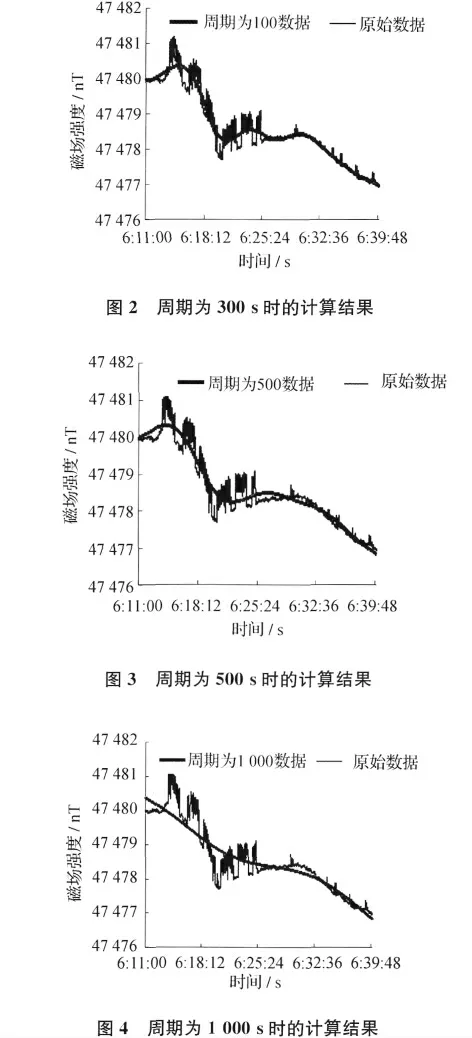
本文通过研究表明,选择不同的截止周期可以为用户提供不同特征的数据,可以满足不同的需求。图1~4为采样间隔为1s的原始数据分别在周期为100s、300s以及500s所对应的结果图,图中细线代表原始数据,粗线代表计算结果。
由图1~4可以看出,采用FFT算法,选取不同的周期提取数据的特征各不相同。图1选用周期为100s,提取数据很好地反映了数据细微的变化,同时也将可能是噪声的误信号带入其中。该数据可以用于物探、地震、磁暴预测等对数据细节要求很高的邻域,并不是数据平滑的最佳截止周期。图2选用周期为300s,提取数据很好地实现了数据的平滑,与图3相比在细节部分对数据的反映更加真实。图4选用周期为1 000s,该数据反映了地磁变化趋势,通过选用合适的滤波门限可以用于地磁日变数据的消噪,但是其也丢失了过多的地磁数据时变特征,不能很好反映整个地磁序列的细部特征。因此,建议确定300s为地磁日变数据平滑的截止周期。同时通过上述研究,分别得出了几种数据截止周期(见表1)。

表1 1Hz采样率原始数据不同的截止周期选择 s

图1 周期为100s时的计算结果
3 试验分析
通常地磁数据的平滑多选用多项式拟合逼近的办法来实现。如果曲线的阶数选择的过小,拟合效果不好;如果曲线的阶数过高,虽然数据点上看到效果好,数据点之间会出现有数据振荡的问题且计算速度很慢效率较低,同时可调节性过小。为验证本文方法的准确性与可靠性以及与传统方法相比较具有的优缺点。本文采用中国西部某地磁日变站2008年某一天的地磁日变原始观测数据作为试验数据。基于文中所述FFT方法及截止周期的确定,选取300s的截止周期,将数据进行平滑,并与5阶多项式模型进行比较(见图5、图6)。
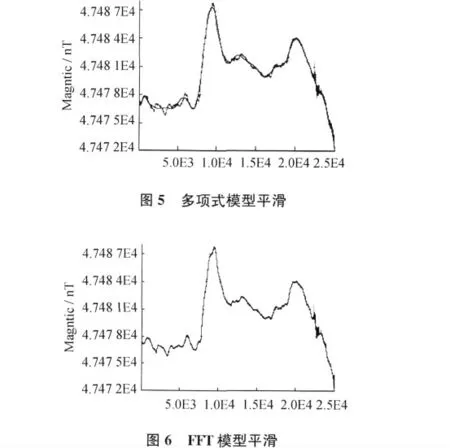
通过图5、图6可以看出,二者在图像上都实现了与原始数据的逼近,均可以对原始地磁序列的平滑处理,但是FFT算法可以更真实地反映数据的变化趋势,与原始数据的趋势吻合的更好。多项式方法的拟合结果虽然也实现了趋势的反映,但是其对图像的一些细部特征未能很好地表达,由图5还可以发现传统算法有一定的时延效应。平滑曲线与原始趋势相比有一定的滞后。
4 结 论
本文通过实验分析得出如下结论:
1)基于FFT数字信号处理技术的地磁日变处理方法是正确和可靠的。用于1Hz采样率的地磁日变数据平滑的截止周期建议选择300s。同时利用该法还可以根据自己的需要对数据进行细部特征提取及消噪。
2)传统的多项式拟合逼近的办法可以实现地磁日变数据的平滑,但是其反映数据细部特征的能力有限,同时还存在一定的滞后性,性能略低于FFT算法。
3)地磁日变数据质量控制是地磁日变数据处理的一个重要环节,在地磁日变数据处理之前,必须进行原始数据的质量控制。
[1]Wang Tanwen.Research on Geomagnetic Field Model.Recent Developments In World Seismology[J].Vol.4.
[2]AN Zhen-chang,XU Yuan-fang,WANG Yue-hua.Derivation and analysis of the main geomagnetic field models in China for 1950-1980.Chinese Journal of Geophysics[J].1991,34(5).
[3]AN Zhen-chang.Review of Geomagnetic Surveys,Geomagnetic Charts and Geomagnetic Field Models in China.Chinese Journal of Geophysics[J].45:189-196.
[4]Gao Jintian,An Zhenchang,Gu Zuowen,Han Wei,Zhan Zhijia,Yao Tongqi.Selections of the Geomagnetic Normal Field and Calculations of the Geomagnetic Anomalous Field.Chinese Journal of Geophysics.48(1):51-62.
[5]Gu Zuowen,An Zhenchang,Gao Jintian,Zhan Zhijia,Yao Tongqi,Han Wei,Chen Bin.Computation and Analysis of the Geomagnetic Field Model In China and ITS Adjacent Area for 2003.Acta Seismologica Sinica[J].28(2):141-149.
[6]Behrooz Kamgar-Parsi,et al.Toward an auto-mated system for a correctly registered bathym etric ch art.IEEE Journal of Oceanic Engineering[J].1989,14(4):314-325.
[7]Zhang Z.Iterative point matching for registration of freeform curves and surfaces.International Journal of Computer Vision[J].1994,13(2):116-152.
[8]John J Leonard,Andrew Bennett.Autonimous Underwater Vehicle Navigation.MIT Marine Robotics Labotics Laboratory Technical Memorandum[J].1998,(1):1-11.
