基于混合粒子群的核磁共振反演算法研究

宋 鹏 王国富

（桂林电子科技大学信息与通信学院，广西 桂林 541000）

核磁共振找水反演是地球物理反演的分支，近年来出现了奇异值分解反演、模拟退火反演等方法研究。目前，粒子群优化算法广泛应用于调度、模式识别、模糊系统控制、盲源分离等领域。在地球物理反演领域，主要应用于波阻抗反演[1]和磁测资料反演[2]中，而在核磁共振反演领域的应用很少。本文在研究核磁共振反演理论的基础之上，应用带非线性约束优化的混合粒子群算法，对核磁共振人工合成数据进行数值反演仿真分析，开拓了粒子群优化算法的新应用领域，同时，为进一步研究核磁共振反演方法提供理论依据。

1 核磁共振找水非线性反演理论

核磁共振找水反演，是将核磁共振数据资料解释成地下水文地质参数，本文主要解释其中的地下含水量分布。它的主要方法可以分为线性反演方法和非线性反演方法两大类。传统的线性反演方法在对地下低电阻介质情况下的数据进行反演时，反演结果精度较差。非线性反演方法可以解决这一问题，非线性反演方法一般采用最优化方法的理论求取地下含水量分布，即使用吉洪诺夫泛函[3]作为最优化的目标函数，目标函数表达式如下所示：

并使目标函数最小化。核磁共振找水非线性反演的

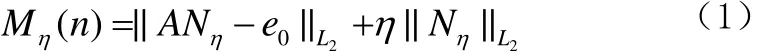
方程中，A为核函数矩阵，e0表示观测到的初始振幅值，Nη即为需要求解的含水量值，是使吉洪诺夫泛函最小的解向量。

2 粒子群反演算法

粒子群反演算法[4]是地球物理非线性反演方法中的一种，其中，粒子群算法（Particle Swarm Optimzation，简称PSO)是Kennedy和Eberhart提出的基于仿生学原理发展起来的智能优化算法。为求得目标函数f(x)达到最优解xp（最小值）的相应x值，应用粒子群算法的具体步骤为：

（1）给定粒子数目n，自变量x的个数m。随机初始化所有粒子的位置xn×m和速度vn×m。

（2）存储当前各粒子的位置（记为）和相应的适应度值，找到的最小值，并记录相应 f( xp)的位置， f( xp)记为xpg。

（3）按照公式（2）和公式（3）更新粒子的速度和位置。公式中，w为惯性权重，c1、c2为正的学习因子， r1和r2为0到1之间均匀分布的随机数。p为当前的个体极小值，pg,ji,j为当前的全局极小值。

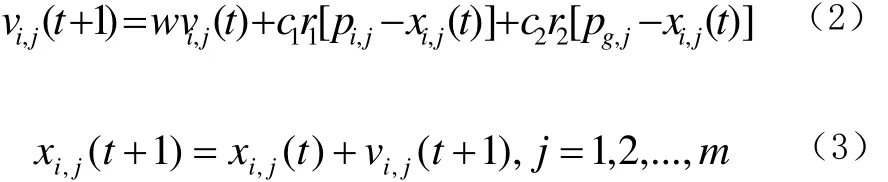
（4）更新后的适应度值f(x)与步骤2中的f(xp)值进行比较，较小值的相应位置作为当前的xp，当前的 f(xp)再与f(xpg)进行比较，较小值的相应位置作为当前的xpg。

（5）给定迭代次数，作为调节粒子速度和位置的次数，若未停止迭代，返回步骤（3）继续搜索，若停止迭代，此时的xpg为最优位置，f（xpg）为最优解。

3 混合粒子群反演算法

为了避免基本粒子群算法陷入局部极小解，引入模拟退火算法[5]，该算法的概率受温度参数的控制，具有概率突跳的能力，概率的大小随温度下降而减小。混合粒子群反演算法的具体步骤如下：

（1）将种群中的各微粒的位置、速度进行随机初始化；

（2）对各个微粒的适应度（相应的函数值）进行评价，存储当前各微粒的位置，设为pi，存储全局最优个体的位置，设为pg；

（3）给定初始温度，根据公式（4）确定各pi的适配值：

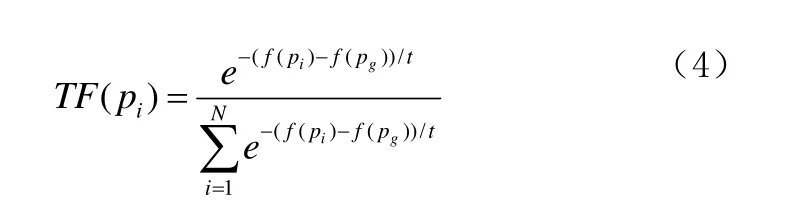
（4）根据轮盘赌机制确定全局最优值的相应粒子位置pgbest，并根据公式（5）和公式（6）更新微粒的速度和位置：

（5）更新各微粒的局部pi值和全局pg值，并进行退温操作；

（6）若满足预设的运算精度或迭代次数，停止搜索，输出最优位置和最优值，否则转到步骤（3）；

为了将粒子群优化算法适用于核磁共振找水反演中，设定非线性约束条件：作为粒子位置的可行域，各粒子在该可行域内调节相应的位置，搜寻最优解。

4 测试函数数值计算

选择 3个常用的测试函数[6]来验证混合粒子群算法的有效性。

函数一：Sphere函数，函数表达式为：

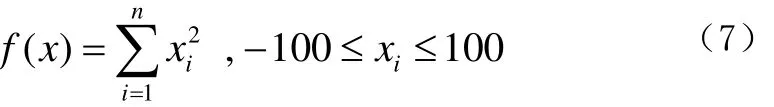
函数一在 xi=0处达到全局极小点，本文计算结果为0.000029465。函数一的迭代过程如图1所示。

图 1 sphere函数迭代过程

函数二：Rosenbrock函数,函数表达式为：

函数二在 xi=1时达到全局极小点，本文利用混合粒子群算法的计算结果为0.9984。函数二的迭代过程如图2所示。

图2 Rosenbrock函数迭代过程

函数三：Rastrigin函数，函数表达式为：

函数三是多峰函数，在 xi=0处达到全局极小点，本文计算结果为0.0000013189。函数三的迭代过程如图3所示。

图3

5 基于混合粒子群反演实验分析

在均匀半空间条件下，假设大回线源线圈的半径为50m，地下电阻率50Ω，地磁倾角60°。对目标函数应用粒子群优化算法进行最优化求解，正演拟合初始振幅如图（a）所示。反演拟合含水量如图（b)所示。

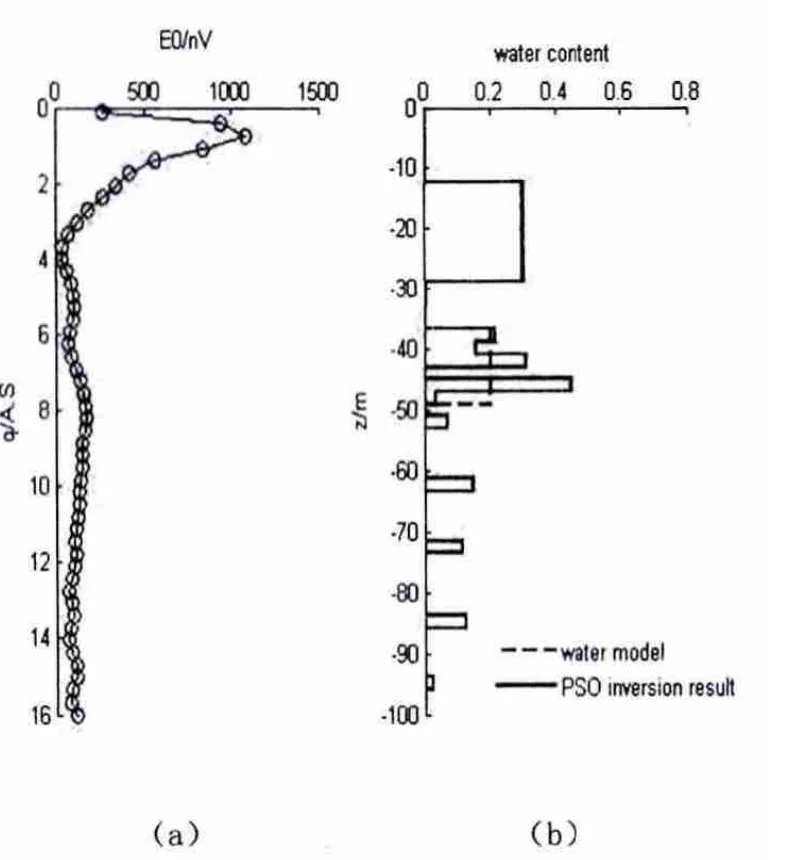
图4 粒子群反演拟合结果

浅水层的反演拟合效果较好，深水层反演拟合效果较差，但是整体的垂直分辨率较高。由此可见，混合粒子群反演算法适合于核磁共振找水反演中。

[1] 易远元,王家映.粒子群反演方法[J].工程地球物理学报,2009,6(4):385-389.

[2] 张大莲,刘天佑,陈石羡,等.粒子群算法在磁测资料井地联合反演中的应用[J].物探与化探,2009,33(5):571-576.

[3] 林君,段清明,王应吉,等.核磁共振找水仪原理与应用[M].北京:科学出版社,2010.

[4] 方伟,孙俊,须文波.一种多样性控制的粒子群优化算法[J].控制与决策,2008,23(8):863-868.

[5] 王华秋,曹长修.基于模拟退火的并行粒子群优化研究[J].控制与决策,2005,20(5):500-504.

[6] 熊勇.粒子群优化算法的行为分析与应用实例[D].杭州:浙江大学,2005.