基于解析模式分解的密集工作模态参数识别

王佐才，任伟新

（合肥工业大学 土木水利学院，合肥 230009）

近年来，结构健康监测和安全评估已成为国内外众多学者致力研究的一个重要课题。而其中关键问题之一是对结构的参数进行有效的识别，这些结构参数又是进一步研究结构灾变机理，结构状态识别以及安全评估的重要基础和依据。因而在过去十多年里，结构参数识别成为了结构健康监测与安全评估的热点研究领域之一[1,2]。传统的参数识别方法又主要包括时域的方法和频域的方法。时域识别方法，其理论基础是线性动力学系统的状态空间方程，无法直接应用于非线性系统的模态参数识别。而频域识别方法的基础是富里叶变换，其基本的假定是信号必须是平稳的，此时将时域信号转换到频率域，没有任何时域的信息。因此，近年来，以小波变换和Hilbert变换（特别是Hilbert-Huang变换）为基础的时频分析方法在结构模态参数识别和损伤检测中受到了广泛的关注[3―10]。

然而，这些方法在分析复杂环境荷载下的结构振动信号时，也遇到了诸多的难题：

（1）无法分离密集的模态响应，特别是具有模态频率叠混(overlapping)的信号；

（2）对于时变的具有模态叠混的结构响应，结构的模态响应也往往存在于多个临近的分解信号中，需要进行进一步的重组。为了解决密集模态的参数识别，国内外的学者也做了相当的研究工作，如：Chen and Xu[11]研究了HHT方法在密集模态结构中模态参数的识别方法，在EMD分解过程中采用间歇检查(Intermittency check)来分离密集模态，利用Hilbert变换识别结构的自振频率和阻尼比。Yang et al.[12]在进行EMD分解前，利用带通滤波器对信号进行滤波预处理，从而把结构的密集模态分离出来。事实上，如果普通的带通滤波器能把每一密集模态都分离出来了，就可以直接利用Hilbert谱分析方法对结构的参数进行识别了。但是，对于非常密集的模态，由于两个频率非常接近，只能选择截止频率对信号进行滤波。然而，利用截止频率滤波，相当于在频率域中乘以了一个矩形函数，在时间域中就会产生较大的波动，特别是对于具有多个密集模态频率的信号，滤波后的信号失真非常明显。

为了解决复杂环境下具有密集模态与频率叠混的非平稳结构响应信号的有效分解，Chen and Wang[13,14]和Wang[15]首次提出了非线性非平稳信号的解析模态分解理论(Analytical Mode Decomposition（AMD）Theorem)，并且成功的识别了自由振动下具有密集模态三自由度的系统。本文，在此基础上，进一步研究以下几个问题：

（1）环境激励下的基于AMD理论与随机减量结合密集模态参数识别问题；

（2）频率密集程度指数和信号时程长度对AMD分解的影响；

（3）通过对附有阻尼器的3层框架的振动台实验验证基于AMD理论的密集模态参数识别方法。

1 基于解析模式分解的密集参数识别理论

1.1 解析模式分解（AMD）

基于Hilbert变换的AMD分解理论的表述如下：对于任意由n个信号分量xdi(t)(i=1，2，…，n)组成的原信号x(t)

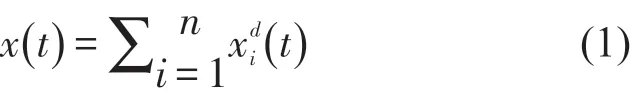
如果它的每一分量的时变频率ω1(t),ω2(t),…ωn(t)满 足 ：|ω1(t) |＜ωb1(t),ωb1(t)＜|ω2(t) |＜ωb2(t)…ωb(n-2)(t)＜|ωn-1(t) | ＜ωb(n-1)(t)，ωb(n-1)(t)＜|ωn(t)|。

其 中ωbi(t)∈(ωi(t),ωi+1(t))(i= 1，2…，n-1)为选取的时变截止频率。那么它的每一信号分量可以解析的给出其中 H[.]为Hilbert变换，为

截止频率的积分。对于频率不随时间变化的信号，式（3）可以简化为

关于解析模式分解的证明见文献[13，14]。根据上述AMD分解的表述，可以设计如图1所示的自适应低通滤波器。AMD的本质是利用Hilbert变换把每一具有特定频率成分的信号解析的分解出来。对于多个时变密集频率信号叠加的复杂信号，AMD通过构造一对具有相同特定时变频率的正交函数，并利用这对时变正交函数与原复杂信号的乘积的Hilbert变换，把任意在频率时间平面内低于正交函数时变频率的信号解析的分解出来。因而，AMD的作用就像是一个自适应时变滤波器。根据上述的方法，可以近似选取出时变的截止频率，从而根据AMD分解原理，设计出各种不同的低通，带通滤波器，应用于结构振动响应信号的分解。对于频率不随时间变化的信号，其截止频率可以根据傅立叶谱中相邻的两个峰值取平均来确定[13]。传统的滤波器由于在频域内利用矩形窗截断，再从频域变换到时域就会产生一个sinc函数与实际函数的积，从而使分解的信号在时域内产生较大的影响。由于解析模式分解是利用Hilbert变化在时域内对信号进行分解，因而分解的信号不会产生类似的影响。

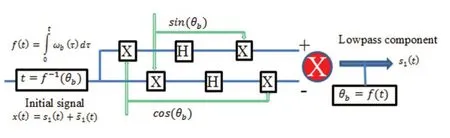
图1 基于AMD分解的自适应低通滤波器Fig.1 Adaptive lowpass filter with AMD

1.2 RDT-AMD方法

工作环境激励的输入信号的频率具有宽带宽的特点，一般可假设为平稳的白噪声，而每一模态响应具有窄带宽的特点，然而由于结构的自振频率本身就非常接近，因此结构的模态响应在外激励下就会产生模态混叠的现象。本文提出RDT-AMD方法，首先利用随机减量技术（RDT）提取出结构的自由振动响应，可以有效的减少模态叠混的影响，然后利用AMD方法对提取出来的自由振动响应进行分解，提取每一自由振动的模态响应，最后，利用最小二乘法识别结构的频率，阻尼比等模态参数。

RDT方法从结构的振动响应中选取相同初始位移，初始速度和相同时间长度的响应作为样本，并且认为在近似白噪声的环境激励下的结构这些振动响应由三部分组成，即初始位移，初始速度，白噪声激励引起的响应，由于结构的白噪声激励响应信号的均值为零，通过对多个样本求平均可以剔除受迫振动部分的响应，剩下的就是自由振动响应。利用RDT求自由振动响应如下

其中xt(ti+τ)是结构环境激励下的具有相同初始位移，初始速度和相同时间长度振动响应样本，ti是第i个样本的开始时间，tSeg是振动响应样本的时间长度，xf(τ)是通过RDT获得的自由振动响应。

对获得的自由振动响应信号xf(t)可以利用AMD进行分解，提取每1阶的模态振动响应对应第p个自由度的第i个分解的模态响应信号(τ)的瞬时幅值A(τ)和瞬时相位角θ(τ)可以类pipi似HHT方法给出

另一方面，结构第p个自由度的自由振动响应可以由模态振形ϕpi和模态坐标gi(τ)(i= 1,2…,n)叠加表示

因此结构的第p和第q个自由的第i阶振形比值可以由AMD分解后信号的幅值获得

2 参数分析

2.1 频率密集程度指数

频率密集程度指数g的定义如下[11]

其中ωi和ωi+1是相邻的自振频率，频率密集程度指数g越小，自振频率就越密集。为了进一步研究AMD方法对密集模态分解的准确性，一个信号分解准确性能量误差指标定义如下

其中(t)和xi,exact(t)分别为第i个分解后的信号分量和实际的信号分量。

为了定量分析频率密集程度对AMD信号分解的影响，选用一个具有密集模态的两层框架做数值模拟。其中激励荷载作用于顶层的高斯白噪声。m1和m2分别为第一和第二层的质量，k1和k2为层间的刚度系数，c1和c2为层间的阻尼系数。本文中假设阻尼为Rayleigh阻尼，每1阶的模态阻尼比均为ζ。第1阶和第2阶自振频率分f1和f2。本文对六组频率密集程度指数进行了研究，主要的结构参数见表1。

对于工作环境激励，输入ρ(t)假定为一均值为零方差为1N高斯白噪声，结构的振动响应时间为1 000 s，采样间隔0.05 s。为了比较分析，模拟了结构在冲击荷载ρ(t)为1N的激励下的自由振动响应，其中自由振动响应的采样时间假设为20 s，采样间隔为0.01 s。利用AMD对工况3自由振动与环境振动分解后的第1阶振动模态响应如图2所示。通过与理论的模态振动响应比较，可以看出，通过AMD分解的第1阶自由振动响应与理论结果十分接近。然而，对于工作环境激励，通过AMD分解的第1阶模态振动响应与理论结果存在着一定的误差。这是由于结构的频率十分接近，在宽带宽的外荷载左右下，结构的模态振动响应是一窄带宽的响应，存在着模态叠混的现象（图3）。从图4中可以进一步看出，第2阶模态响应对第1阶模态响应有着显著的影响。

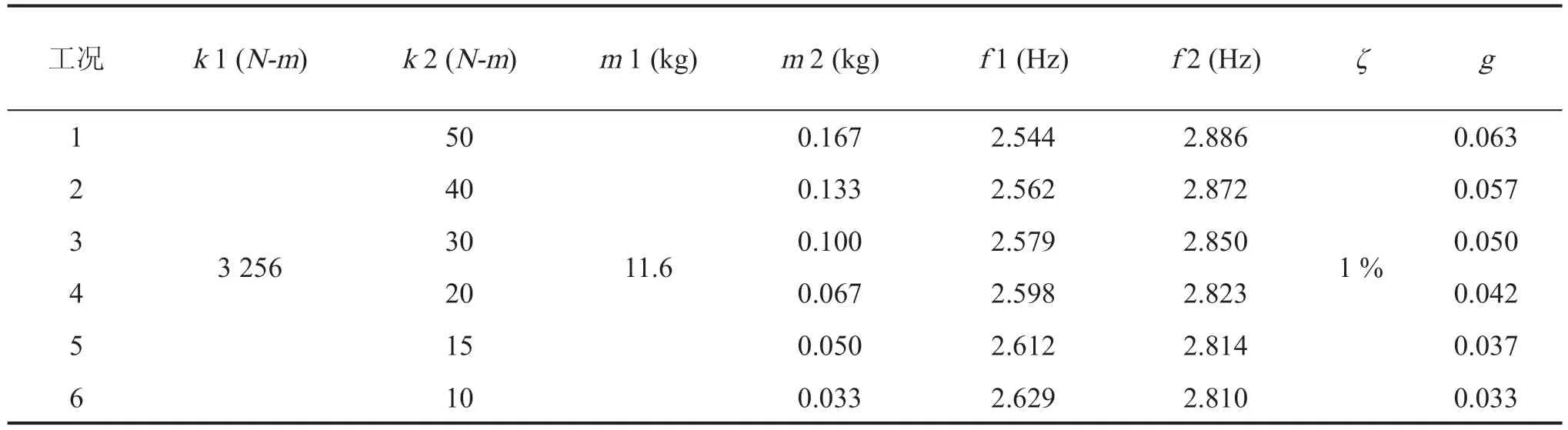
表1 两层框架的结构参数Tab.1 Properties of the two-story building

图2 理论上的第1阶模态响应与实际分解后第1阶模态响应Fig.2 Exact and decomposed responses of the first mode

图3 理论上第1和第2阶模态响应的傅立叶谱Fig.3 Fourier spectra of the exact responses of modes 1 and 2

随着频率密集程度指数g从0.033变化到0.063，文中定义的对应的前2阶模态响应分解的能量误差指标如图4所示。当g=0.033，对于自由振动，前2阶模态响应分解的能量误差指标分别为7.5%和1%左右。然而，对于环境振动，前两阶模态响应分解的能量误差指标分别为88%和10%。图4进一步显示环境振动的能量误差指标比自由振动的能量误差指标明显要大，说明了结构的模态振动响应是一窄带宽的响应，存在着模态叠混的现象，从图3中可以看出，第2阶模态响应对第1阶模态响应有着显著的影响，因此环境激励下的第1阶模态响应分解的能量误差指数超过了50%，然而，从图3中可以看出，第1阶模态响应对第2阶模态响应相对较小。因此，环境激励下，第2阶模态响应分解的能量误差指数不超过10%。从图2至图4可以看出，环境振动下的结构模态响应存在着模态叠混的现象，而相应的自由振动响应的模态叠混程度要低的多，因此通过AMD分解的自由振动相应误差也相应小得多。因此对于白噪声激励下的环境振动响应，可以通过随机减量方法获得相应的自由振动响应，从而可以有效的减少模态叠混的影响。

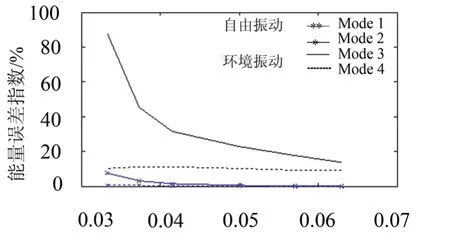
图4 自由振动与环境振动下的能量误差指标Fig.4 Energy error indices with free and ambient vibration

2.2 信号时程长度

由于通过RDT提取的结构自由振动响应信号的时程长度比实际的信号时程长度要短得多。由于信号的时程长度变短，其傅立叶谱的频率精度也大大降低了，因此有必要研究AMD分解受时程长度的影响进行分析。为了进一步量化时程长度对AMD信号分解的影响，以2.1中的两层框架自由振动为例，其中频率密集程度指数g=0.05。假设顶层的自由振动响应x2(t) 的时程长度分别为：1，2，3，… 20秒。采样时间间隔为0.01 s。AMD分解的截止频率取傅立叶谱中两相邻峰值的均值。对于不同时程长度下分解后信号与理论上结果比较后能量误差指标如图5所示。显然，当自由振动的时程长度为1秒时，AMD分解后的信号能量误差指标也不超过20%。当自由振动的时程长度为7 s时，能量误差指标就小于5%。如图5所示，AMD分解的后信号的能量误差指标总体上随着时程的增长而减少。

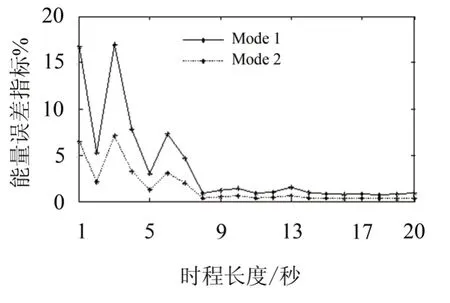
图5 自由振动下的能量误差指标随时程长度变化的关系Fig.5 Energy error index under free vibration with various time duration

3 数值模拟

为了验证RDT-AMD方法识别结构的密集模态参数，本文利用同文献[11]相同的36层框架和4层的附属层。结构每一层的质量和层间的刚度分别为1.29´106kg和1.0´109N/m。附属层的质量是主体层质量的2%，而附属层间的刚度为主体层间刚度的0.03%。结构的前4阶频率分别为0.184，0.196，0.542，and 0.573 Hz。结构的阻尼假设为经典阻尼，其中前4阶模态的阻尼比均为1%，而其它高阶模态的阻尼比为零。结构承受均值为零方差为0.001 g的高斯白噪声加速度激励。结构顶层的加速度响应为假想测试获得的响应，其中采样频率为20 Hz，其顶层加速度的傅立叶谱如图6所示。

图6 数值模拟的顶层加速度响应的傅立叶谱Fig.6 Fourier transform of the acceleration at the top of appendage

如图6所示，结构的第1阶与第2阶，以及第3阶和第4阶模态存在模态叠混的现象，首先可以简单的选择截止频率为0.4 Hz，利用AMD把第1和第2模态响应分离出来，然后选择截止频率为0.7 Hz，利用AMD把第3和第4阶模态响应从剩下的信号中进一步分离。由于第1与第2阶，以及第3与第4阶模态具有模态叠混。

为了进一步分离出每1阶模态响应，首先利用RDT技术提取其自由振动，图7所示即为提取的自由振动响应。然后再利用AMD把每1阶模态响应分离出来，再利用最小二乘方法拟合瞬时幅值和瞬时相位直线，利用拟合后直线的斜率求得结构的频率和阻尼比。利用AMD分离出来的每1阶模态响应的瞬时幅值A与瞬时相位θ(ρ i=1，2，3，and 4)以及拟合的最小二乘直线。根据拟合直线斜率所求得的每1阶频率和阻尼比见表2。表2的结果表明，利用本文方法识别出来的频率和阻尼比误差分别小于1%和6%，因此本文提出的RDT-AMD方法可以较为准确的识别出结构的密集模态参数。

图7 RDT提取的自由振动响应Fig.7 Extracted free response using RDT

4 实验验证

为了进一步验证RDT-AMD方法的对密集模态参数识别的有效性，对一个顶层装有质量阻尼器的三层的钢结构框架进行了振动台实验(如图8)。钢结构框架的长1.22 m，宽0.61 m，高2.54 m。阻尼器的自振频率与结构的第一自振频率接近，因此结构体系具有两个密集的模态频率。结构和阻尼器的其它参数见表3所示。为了比较分析，结构的激励分别设计成20 s时长的具有零均值和0.001 g(g为重力加速度)方差的高斯白噪声和经过时间压缩3/4的1952年Taft地震波。测得的结构的顶层的加速度响应信号（采样频率100 Hz）和其傅立叶谱分别如图9和图10所示。

图8 三层框架振动台实验Fig.8 Shake table test of a 3-story steel frame

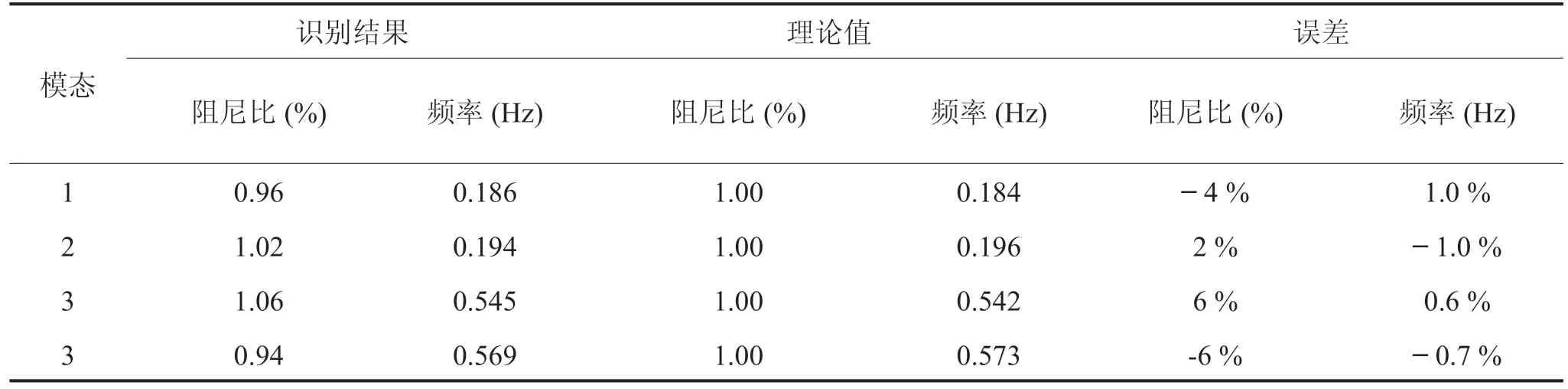
表2 识别出的结构自振频率与阻尼比Tab.2 Identified natural frequency and damping ratio of the building-appendage system

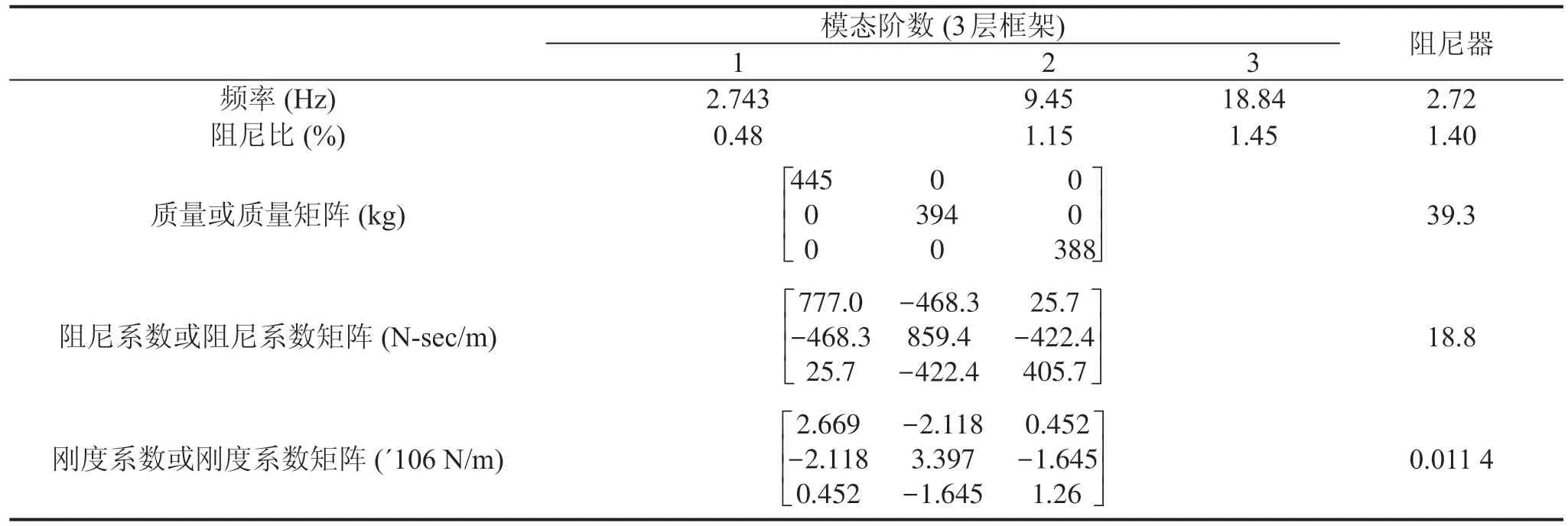
表3 结构框架与阻尼器参数Tab.3 Properties of steel frame and damper

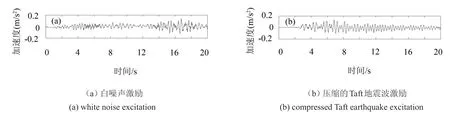
图9 测得的顶层加速度响应时程Fig.9 Measured top floor accelerations of the structure

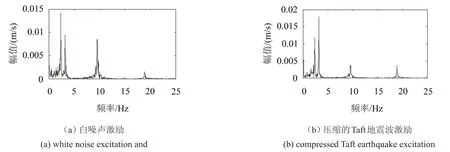
图10 测得的顶层加速度响应时程的傅立叶谱Fig.10 Fourier spectra of the measured top floor accelerations

对于第1阶和第2阶模态响应，利用RDT提取了时长为3.5 s的自由振动响应，每1阶的自由振动响应由AMD方法进一步分解获得。最后利用最小二乘方法拟合瞬时幅值和瞬时相位直线，利用拟合后直线的斜率求得结构的频率和阻尼比。利用AMD分离出来的每1阶模态响应的瞬时幅值A与瞬时相位θ(p i=1，2)以及其拟合的最小二乘直线。根据拟合直线斜率所求得的每1阶频率和阻尼比见表4。表4的结果表明，在不同激励荷载左右下，利用本文方法识别出来的结构模态参数非常接近，因此本文提出的RDT-AMD方法可以有效的识别出结构的密集模态参数。

表4 识别出的结构自振频率与阻尼比Tab.4 Identified natural frequencies and damping ratios from the top floor acceleration

5 结语

本文提出了工作环境振动下结构密集模态参数识别的RDT-AMD方法。通过对结构密集程度指数，时程长度等参数分析，以及具有密集模态参数的36层框架的数值模拟，和3层框架的振动台实验验证，可以得出如下结论：

（1）RDT能有效的提取结构工作环境振动下的自由振动响应，可以减少具有密集模态结构的模态响应叠混的影响。由于AMD优越的信号分解能力，对频率非常密集和时程很短的信号仍然能够较为准确的分解出每一信号分量。因此，本文提出的RDTAMD方法，在结构的频率非常密集时，仍然能够较为准确的识别出结构的模态参数；

（2）本文通过对频率密集程度指数和时程长度的参数分析，说明了AMD具有较为优越的信号滤波功能；

（3）通过数值模拟和振动台实验的验证，本文提出的RDT-AMD方法能够较为准确有效的识别结构在白噪声或者地震荷载等激励下的密集模态参数。

[1]Doebling S.W.,Farrar C.R.,and Prime M.B.,A Summary Review of Vibration-Based Damage Identification Methods[J].Shock and Vibration Digest,1998,Vol 30,pp.91-105.

[2]Sohn H.,Farrar C.F.,Hemez F.M.,Shunk D.D.,Stinemates D.W.Nadler B.R.,and Czarnecki J.J.A Review of Structural Health Monitoring Literature:1996-2001[M].Report LA-13976-MS Los Alamos National Laboratory,Los Alamos,N M,USA,2004,301 pp.

[3]Gurly K.and Kareem A.Application of wavelet transform in earthquake,wind,and ocean engineering[J].Journal of Engineering Structures,1999,21(2),149-167.

[4]Hou Z.,Noori M.and Amand R.S.Wavelet-based approach for structural damage detection[J].Journal of Engineering Mechanics,2000,126(7),677-683.

[5]Staszewski W.J.Identification of damping in MDOF systems using time-scale decomposition[J].Journal of Sound and Vibration,1997,203(2),283-305.

[6]Ruzzene M.,Fasana A.,Garibaldi L.and Piombo B.Natural frequencies and damping identification using wavelet transform:application to real data[J].Mechanics Systems and Signal Processing,1997,11(2),207-218.

[7]Liu B.,Riemenschneider,S.and Xu Y.Gearbox fault diagnosis using empirical mode decomposition and Hilbert spectrum[J].Mechanic Systems and Signal Processing,,2006,20(3),718-734.

[8]Chen H.G,Yan Y.J.and Jiang J.S.Vibration-based damaged detection in composite wingbox structures by HHT[J].Mechanic Systems and Signal Processing,2007,21(1),307-321.

[9]Feldman M.Non-linear system vibration analysis using Hilbert transform-I:free vibration analysis method[J].Mechanical Systems and Signal Processing,1994 8(2),119-127.

[10]Feldman M.Non-linear free-vibration identification via the Hilbert transform[J].Journal of Sound and Vibration,1997,208(3),475-489.

[11]Chen J.and Xu Y.L.Identification of modal damping ratios of structures with closely spaced modal frequencies[J].Structural Engineering and Mechanics,2002,14(4),417-434.

[12]Yang J.N,Lei Y,Pan S.and Huang N.System identification of linear structures based on Hilbert-Huang spectral analysis,Part I:Normal modes[J].Earthquake Engineering and Structural Dynamics,2003,32(9),1443-1467.

[13]Chen G.D.and Wang Z.C.A signal decomposition theorem with Hilbert transform and its application to narrowband time series with closely-spaced frequency components[J]. Mechanic Systems and Signal Processssiinngg,2012,28,258-279.

[14]Chen G.D.and Wang Z.C.Response to the letter to editor by Dr.M.Feldman Entitled“A signal decomposition or lowpass filtering with Hhilbert transform”[J].Mechanic Systems and Signal Processing,2011,25(8)3204-3204.