驾驶员行为对交通噪声的影响

朱丽颖，李贤徽

（环境噪声与振动北京市重点实验室,北京市劳动保护科学研究所,北京,100054）

针对道路噪声问题，我国目前采取的技术防治对策主要包括噪声源对策、噪声传播途径对策以及受声点对策。其中噪声源对策主要是通过对车辆及路面结构进行优化改造从源头降低噪声。值得注意的是，在由人、车、路三要素组成的道路交通系统中，具有复杂认知活动与协同能力的驾驶员是道路交通系统的信息处理者和决策者，在协调和控制交通三要素的各个环节中起着举足轻重的作用。在道路与车辆等客观因素既定的情况下，驾驶员的行为特性直接决定了道路交通系统的状态，从而间接影响道路交通的噪声水平。因此，从道路噪声角度对驾驶员行为展开研究，了解驾驶员行为对交通噪声的影响情况，是解决道路噪声问题的又一有效手段。由于驾驶员行为不仅与驾驶员自身心理、生理特点相关，同时还随周围路况变化而改变，因此采用常规的实测方法进行研究存在很大难度，而目前交通流仿真技术发展成熟，为深入研究驾驶员行为对交通噪声的影响提供了可能。现代交通流理论认为，可以通过对驾驶员个体微观层次上的详细建模来重现宏观层次上的交通流现象，即通过微观交通仿真反映道路交通系统的运行状态。微观交通仿真即以单个车辆为基本单位，描述交通流的变化特征，从微观层次分析车辆的跟驰、换道、超车等驾驶行为，通过车辆单元之间的相互制约关系以及车辆周围的道路环境和几何条件，来确定车辆的运行特征，如车辆的位置、运行速度、加速度等。近年来随着交通微观仿真技术的发展，微观交通流仿真正逐渐成为研究道路噪声的重要手段。Leclercq等人利用交通流微观仿真方法对信号交叉口、环形交叉口等交通系统噪声进行了较为深入的研究，并通过对比分析发现结合交通流微观仿真的交通噪声模型计算精度优于传统模型[1―3]。李峰等人根据能量叠加原理提出了基于微观交通仿真的交通噪声模拟方法[4]，并应用该方法针对交通噪声相关问题展开了研究，得到以下结论：通过微观交通流仿真方法计算得到的道路等效声级LAeq与实测值的误差小于2 dB[5]；从噪声对人的干扰角度考虑，噪声污染级随车流量的增大呈现出先增大后减小的特征；对于交叉口，信号控制下的等效声级低于无控制下的等效声级[6]。

从上述国内外研究现状可知，基于仿真方法的交通噪声研究已取得了一定成果，然而道路交通系统的核心组成部分——驾驶员对交通噪声的影响情况却少有人研究。因此，本文以VISSIM微观交通仿真软件为平台，选用Wiedemann驾驶员行为模型，结合日本ASJ道路交通噪声排放模型[7]，对不同驾驶员行为进仿真实验，探讨驾驶员行为对交通噪声的影响。

1 方法与模型

1.1 研究方法

从可行性角度考虑，通过实测实验的方法研究驾驶员行为对交通噪声的影响存在很大难度，因此本文采用交通流微观仿真的方法进行研究。具体研究方法如下：首先确定所要研究的实验变量与评价指标即驾驶员行为变量与输出数据，而后根据仿真实验特点、所需输出数据选定合适的微观交通流仿真软件，利用微观交通流仿真软件建立研究区域的微观仿真模型，然后结合相应的交通噪声排放模型计算指定接收点处的噪声或指定区域的噪声能量排放情况，最后在驾驶员行为敏感性分析的基础上对较为敏感的重点驾驶员行为展开分析。

驾驶员行为的研究需要精细到车辆个体。因此，本文选用驾驶员行为模型较为成熟、应用较为广泛的微观交通仿真系统VISSIM作为微观交通流仿真软件，通过计算不同驾驶员行为参数下交通噪声的情况研究驾驶员行为对交通噪声的影响。

1.2 基本模型

（1）交通噪声计算模型

目前已有的交通噪声单车模型多为车辆行驶速度的回归模型，然而对于相同车速，处于稳定运行状态与处于频繁加减速状态的车辆所产生的噪声并不相同。为此，本文选用能够较好反映这一现象的日本ASJ-RTN 2008单车噪声排放模型。

参考日本ASJ-RTN 2008单车噪声排放模型，当不考虑路面材质、道路坡度等因素时，A计权声功率级Lw(i,j)可表示为

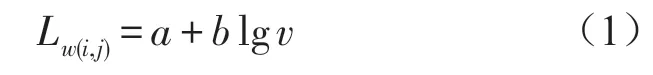
其中v为车辆的运行速度，a、b为与车辆类型、车辆运行状态相关的回归系数，取值办法如表1所示。将车辆分为稳定与非稳定运行两种状态：当车辆位于高速公路或远离交叉口处，能够以最高档行驶时认为该车辆处于稳定运行状态，其速度变化区间为40 km/h至140 km/h；其他情况认为该车辆处于非稳定运行状态，速度变化区间为1 km/h至60 km/h。对于某一车辆类型，不同运行状态对应不同的a、b取值。此外，当接近信号灯交叉口，车辆从稳定状态进行减速停车时或者以大于60 km/h的速度进行加速时，a、b的取值参考稳定状态。非稳定状态下，当速度小于10 km/h大于1 km时，v取10 km/h计算；当速度小于1 km/h时，认为其声功率为零。

表1 系数a、b取值Tab.1 The value of coefficients a and b

将道路上行驶的单车视为半自由声场中的点声源，路网上某辆单车在接收点位置的A计权声压级Li,j与A计权声功率级Lw(i,j)的关系可表示为

其中Lw(i,j)为第i秒钟第j辆车在道路上的A计权声功率级，单位为dB；ri,j为该车辆与接收点的距离，单位为m；ΔLcor(i,j)为与天气、地面吸收等因素相关的修正系数，单位为dB。不考虑天气影响、地面吸收因素时，（2）可简化为

第i秒钟路网上所有车在观测点处的噪声为

式中mi为i秒钟路网上的车辆数量。

那么，一段时间在观测点上接收到的噪声等效值为

式中T为计算时间，单位为s。

从能量角度，第i秒钟第j辆车的声功率Wi,j表示为

其中参考声功率W0=10-12w。

一段时间内研究区域所有车辆所产生的噪声能量E为

其中m为计算时间，n为第i秒钟区域的车辆数，将（6）代入（7），则有

定义单位出行里程的噪声能量排放量e为研究区域在一段时间内完成单位出行里程所产生的噪声能量，则e表示为

其中si,j为第i秒钟第j辆车在研究区域所行驶的里程。

（2）驾驶员行为模型

生理—心理模型也称反应点模型（Action Point Models）简称AP模型，该模型将刺激抽象为前后车之间的相对运动，是与实际最为一致、最能够描述大多数驾驶行为的驾驶员模型类型。本文选用发展成熟、广泛应用于实践的典型AP模型—德国Wiedemann模型[8,9]作为载体展开驾驶员行为对交通噪声的影响研究。

Wiedemann模型根据实测及调研数据，认为驾驶员的驾驶行为是一个生理—心理互相作用、互相制约、互相影响的过程，充分考虑了驾驶员的生理、心理因素对驾驶行为的影响制约。该模型将驾驶员行驶状态分为自由驾驶、接近、跟随、刹车四种类型。模型认为，对于每一种驾驶模式，后车的加速度均由前后车的速度差、车间距离以及驾驶员和车辆的个性特征所决定。当驾驶员达到了某个以速度差和距离表达的阈值时，他将从一种驾驶状态转换到另一种驾驶状态。

VISSIM应用一系列的驾驶员行为参数描述了上述过程，不考虑用来协调仿真精度与仿真速度的相关参数，本文将研究跟驰行为、车道变换、横向行为以及信号反应四类15个驾驶员行为对交通噪声的影响。本文参考已有关于Wiedemann驾驶员行为模型的研究[10―12]，取定各驾驶员行为参数可能的变化范围。

2 结果与讨论

2.1 道路噪声对驾驶员行为的敏感性分析

2.1.1 实验对象

本文选取北京市一长为1.7 km的路段作为仿真路网。该路网包括两个交叉口，交叉口间相距1.2公里。仿真路段两交叉口间共双向8车道，交叉口渠化情况为：交叉口1东进口道方向左转2车道、直行3车道、右转1车道；南进口道方向左转2车道、直行3车道、右转1车道；西进口道方向左转2车道、直行3车道、右转1车道；北进口道方向左转2车道、直行3车道、右转1车道。交叉口2东进口道方向左转1车道、直行3车道、右转1车道；南进口道方向左转2车道、直行3车道、右转1车道；西进口道方向左转1车道、直行3车道、公交专用道1车道、右转1车道；北进口道方向左转2车道、直行3车道、右转1车道。

2.1.2 敏感性分析

考虑到不同道路运行状态下的驾驶员行为的差异性，本文在拥堵状态和非拥堵状态两种道路状态下对上文选定的驾驶员行为参数进行敏感性分析。

研究驾驶员行为参数ak的敏感性，首先令其余各参数取默认值固定不变，令参数ak在其可能的范围内变动，通过仿真计算得到一组路旁接收点处的LAeq值，则该组LAeq值的变化范围以及其最大值与最小值之差反映了参数ak对道路噪声的影响程度。对所有驾驶员行为参数进行仿真计算，结果如表2所示。

首先从表2可以看出，道路在非拥堵状态下，驾驶员行为对交通噪声的影响微小，平均仅为0.11 dB，“协调刹车的最大减速度”影响最大也仅为0.22 dB。当路网处于非拥堵状态时，道路车辆密度低，换道、跟驰等行为出现频率小，基本处于自由行驶状态，因此道路交通状态受驾驶员行为影响微小，从而交通噪声基本不受驾驶员行为影响。与非拥堵状态的结果相反，当道路处于拥堵状态下，某些驾驶员行为会对交通噪声产生较大影响，平均为0.59 dB，“暂时走神持续时间”影响最大达到2.07 dB。因此可知，非拥堵状态下交通噪声对驾驶员行为的敏感度较低，研究拥堵状态下驾驶员行为对交通噪声的影响更具实际意义。

从表2中还易看出，车道变换与横向行为两类驾驶员行为对交通噪声的影响均比较小，其中车道变换类驾驶员行为在拥堵状态下对交通噪声的影响仅为0.4 dB左右，而横向行为对交通噪声的影响为零。相比较而言，跟驰行为以及信号反应对交通噪声的影响则更为明显，两类驾驶员行为对交通噪声的影响区间均值分别为1.43 dB与0.89 dB，两类参数中一半以上参数对交通噪声的影响大于1 dB。由此可知交通噪声对跟驰行为以及信号反应类参数较为敏感，而受换道及横向行为的影响较小。

表2 非拥堵及拥堵状态下敏感性分析结果Tab.2 The results of sensitivity analyses in congestion condition and non-congestion condition

综上所述，当路网处于畅通状态下时，驾驶员行为对交通噪声的影响极小。当路网处于拥堵状态时，交通噪声对跟驰行为以及信号反应的敏感度较高。

2.2 敏感驾驶员行为对噪声排放的影响分析

根据上文的敏感性分析结果，驾驶员行为对于非拥堵状态下的交通噪声影响不大，同时车道变换与车辆横向行为也不对交通噪声造成较大影响，因此本文将对拥堵状态下跟驰行为以及信号反应两类驾驶员行为与交通噪声、噪声能量排放的关系进行进一步分析。

2.2.1 跟驰行为

车辆跟驰行为指当无换道条件或不需要换道时，行驶车队中后车对前车速度变化进行反应、跟随前车行驶的驾驶行为。在驾驶员行为模型中，驾驶员跟驰行为主要受到“暂时走神持续时间”以及“平均安全距离”两个参数影响。由表2可知，虽然“平均安全距离”对道路噪声存在一定影响，但其影响尚不足1 dB，因此仅对“暂时走神持续时间”这一参数进行详细分析。

暂时走神指后车驾驶员在一段时间内不对前车的驾驶行为（紧急刹车除外）做出反应，暂时走神持续时间即为该段时间的持续长度。图1为驾驶员暂时走神持续时间从0 s到10 s的11组仿真分析结果，其中图1（a）为位于路段、交叉口进口以及交叉口出口3个位置接收点处的等效连续A声级的仿真分析结果，图1（b）为仿真时间内仿真区域的噪声能量排放总量以及单位出行里程的噪声能量排放量的仿真分析结果。

由暂时走神持续时间参数的LAeq分析结果可以看出，无论是在交叉口附近还是在路段位置，交通噪声都随暂时走神持续时间的延长而降低，当暂时走神持续时间达到10 s时，三个位置的噪声值分别较无走神时的噪声降低1.77 dB、2.07 dB以及1.59 dB。在仿真路网中，将每辆车视为独立声源，随着驾驶员暂时走神持续时间的延长，路网的通行能力必然随之下降，路网中的声源数量自然也随之减小，整体噪声水平降低。暂时走神持续时间参数的区域噪声排放总能量情况也呈现相同规律，随着暂时走神时间的延长，表示研究区域噪声排放总能量的点状柱状图逐渐降低，由无走神时的14 375 J降至12 606 J。与LAeq和区域噪声排放总能量的分析结果相反，如图1（b）噪声能量排放分析结果中折线所示，单位出行里程噪声排放能量随暂时走神持续时间的延长而升高，当暂时走神持续时间达到10 s时，每完成1 km里程的出行需比无走神时多排放约0.1 J的能量。因此，虽然从等效连续声级以及噪声能量排放总量角度考虑，噪声随暂时走神持续时间的延长而减小，但是随着暂时走神时间的延长，路网的通行能力、整体效率随之降低，完成相同出行里程所排放的噪声能量却呈上升趋势。

图1 暂时走神持续时间仿真分析结果Fig.1 Simulation results for temporary lack of attention

2.2.2 信号反应

信号反应指当车辆接近信号灯时，其安全距离的变化情况。在驾驶员行为模型中，驾驶员的信号反应情况主要通过安全距离降低系数、信号反应距停车线距离（上游）、信号反应距停车线距离（下游）三个参数进行描述。由于在敏感性分析中信号反应距停车线距离（下游）参数对噪声的最大影响仅为0.45 dB，因此不对该参数进行深入研究，只讨论安全距离降低系数与信号反应距停车线距离（上游）两个参数对交通噪声的影响。

安全距离降低系数指当车辆靠近停车线时安全距离缩减的倍数，系统默认值为0.6。图2为安全距离降低系数从0.1到1的10组仿真分析结果。

图2 安全距离降低系数仿真分析结果Fig.2 Simulation results for safe distance reduction factor

由安全距离降低系数的LAeq分析结果可以看出，以0.6为分界线，当安全距离降低系数小于0.6时，该参数对研究路网的等效连续A声级的影响微小，当安全距离降低系数大于0.6时，路段以及交叉口进出口处的等效连续A声级均随该参数的增大而降低。当安全距离降低系数为1时，三个位置的等效连续A声级平均较安全距离降低系数为0.6时低0.7 dB。从噪声能量排放角度，该参数对区域噪声排放总能量的影响较小，而对单位出行里程噪声排放能量的影响较为明显。同样以0.6为分界，当安全距离降低系数大于0.6时，单位出行里程噪声排放能量随该参数的增加由0.87 J/km增大到0.89 J/km。

信号反应距停车线距离（上游）指车辆开始减小安全距离的位置与信号灯停车线的距离，系统默认值为100 m。图3为信号反应距停车线距离（上游）从20 m到200 m的10组仿真分析结果。

由信号反应距停车线距离（上游）的LAeq分析结果可以看出，当信号反应距停车线距离（上游）小于100 m时，路段以及交叉口进出口处的等效连续A声级随该参数的增大而增大，而该参数大于100 m时的5组仿真分析结果基本没有差别。由于交叉口进口与出口处的接收点与停车线距离均在30 m以内，只要车辆在距停车线30 m之外开始缩减安全距离，这两个位置就不会受信号反应距停车线距离（上游）这一参数的影响，因此该参数对于交叉口进出口处两个位置接收点的影响明显小于对路段位置的接收点的影响。从噪声能量排放角度，10组仿真结果间的区域噪声排放总能量在14 000 J到14 500 J间波动，无明显变化规律。而单位出行里程噪声排放量则随该参数的增大呈降低趋势，当参数取值20 m至100 m时尤为明显。

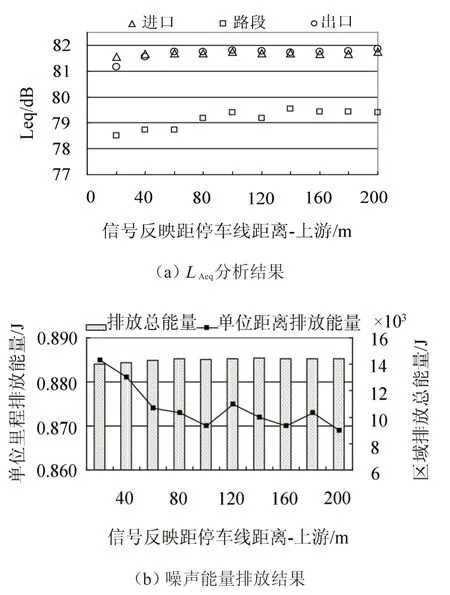
图3 信号反应距停车线距离（上游）仿真分析结果Fig.3 Simulation results for start upstream of stop line

3 结语

本文通过仿真实验以及对实验数据的处理分析，得出以下结论：

（1）当道路处于非拥堵状态时，驾驶员行为对交通噪声的影响极小，最高仅为0.22 dB；而当道路处于拥堵状态时，跟驰行为以及信号反应行为能够对交通噪声产生一定影响，最高可达2.07 dB；

（2）从接收点处等效连续A声级角度，道路交通噪声随驾驶员暂时走神持续时间以及信号灯附近安全距离降低系数的增大而减小，随信号反应距停车线距离（上游）的增大而增大；

（3）从区域噪声能量排放总量角度，噪声排放总能量随驾驶员暂时走神持续时间以及信号灯附近安全距离降低系数的增大而减小，不随信号反应距停车线距离（上游）的改变发生明显变化；

（4）从单位出行里程噪声排放能量角度，单位出行里程噪声排放能量随驾驶员暂时走神持续时间以及信号灯附近安全距离降低系数的增大而增大，随信号反应距停车线距离（上游）的增大而减小。

[1]E.Chevallier,A.Can,M.Nadji,L.Leclercq.Improving noise assessment at intersections by modeling traffic dynamics.Transportation Research Part D 14(2009)100-110.

[2]E.Chevallier,L.Leclercq,J.Lelong,R.Chatagnon.Dynamic noise modeling at roundabouts[J].Applied Acousttiiccss,,70(2009)761-770.

[3]Arnaud Can,Ludovic Leclercq,Joel Lelong,Jerome Defrance.Accounting for traffic dynamics improves noise assessment:Experimental evidence[J].Applied Acoustics,70(2009)821-829.

[4]李 锋，蔡 铭，刘济科.基于微观交通仿真的交叉口交通噪声模拟方法[J].环境科学与技术，2010，33(5)：179-182.

[5]李 锋，蔡 铭，刘济科，余 志.行人过街信号控制路口交通噪声动态模拟与特性分析[J].环境科学学报，2011，31(2)：424-429.

[6]李 锋，刘济科，蔡 铭，余 志.信号控制对交通噪声的影响分析[J].噪声与振动控制，2010，30(6)：109-113.

[7]Kohei Wamamoto.Road traffic noise prediction model“ASJ RTN-Model 2008”:Report of the reserch committee on road traffic noise[R].2010 The Acoustical Society of Japan.2010:8-11.

[8]Wiedemann,R.Simulationdes Straßenverkehrsflusses.Schriftenreihe desInstituts für Verkehrswesen der Universität Karlsruhe,(1974),Heft 8.

[9]Wiedemann,R.Modeling of RTI-Elements on multi-lane roads.In:Advanced telematics in road transport edited by the Commission of the European Community,(1991),DG XIII,Brussels.

[10]Yu L.,X.Li,and Z.Zhuo.A genetic algorithm-based approach to the calibration of vissim using gps data.Proceedings of the Eighth International Conference on Applications of Advanced Technologies in Transportation Engineering(AATT2004),Beijing,China,May 26-28,20004,pp.406-411.

[11]Lownes N.E.,and R.B.Machemehl.Sensitivity of simulated capacity to VISSIM driver behavior parameter modification[C].85 th Transportation Research Board Annual Meeting CD-ROM,Washington,D.C.,Jan.2006.

[12]Menneni S.,C.Sun,and P.Vortisch.Michrosimulation calibration using speed-flow relationships[C].87th Transportation Research Board Annual Meeting CDROM,Washington,D.C.,Jan.2008.