高精密厂房中高精密平台控制仿真模拟

刘 洁，史 霄,刘红军

（1.郑州航空工业管理学院，郑州 450015；2.哈尔滨工业大学 深圳研究生院，广东 深圳 518055）

随着科学技术的发展，超精密及超精细加工产业越来越受关注，高科技厂房通过传统的隔震已无法满足超精密及超精细加工产业的生产需求。根据该产业对生产环境要求的精密程度，需要在厂房楼板上设置高精密设备平台来保障该产业的生产。因此，该超精密平台成为产品研发的基础，如何提高平台的微振动控制效果成为近年来的研究热点[1―6]。Fujita T等人运用压电陶瓷作动器对微振动平台进行多自由度微振动控制研究[7]。Nakamura Y等人设计了六个自由度的实验平台，应用超磁致伸缩作动器对微振动平台进行了六个自由度的理论及实验研究[8]。我国的张春良在其博士论文中对六个自由度进行了理论设计，并对Z方向进行了一个自由度的试验研究[9]。虽然针对六个自由度微振动控制国内外都作了一定的理论及实验研究，但是由于超磁致伸缩作动器具有较强的非线性特性，使得控制精度受到一定制约。因此Xu[10]等人考虑到这个制约因素，将一个作动器模型组合进控制系统中，对在X方向上的单自由度隔振平台进行混合控制模拟分析。陶帅等人[11]以单自由度隔振平台为对象对压电致动器建立了等效力学模型并对模型提出了改进，并取得了较好的控制效果。

本文将在现有研究的基础上，通过搭建多自由度微振动平台，建立超磁致伸缩作动器非线性模型及其逆补偿模型，进一步考虑在平台控制系统多自由度方向上植入多个作动器模型，对微振动平台进行混合控制研究。其研究成果将为精密仪表、精密测量设备和精密加工设备等高精度隔振平台系统提供理论、数值仿真和实验依据。

1 多自由度平台系统

图1 多自由度混合隔振系统的结构简图Fig.1 The diagram for the MDOF hybrid vibration isolation system

设计的多自由度混合隔振系统结构简图如图1所示。平台尺寸为长700 mm、宽500 mm、高12 mm。质量为32.76 kg，平台上允许操作荷载32.76 kg。振系统对中高频干扰如：高精密仪器的运转、轨道交通的行驶、以及人员走动等引起的地面振动，具有良好的隔振效果；而且对低频干扰，如由周围声音、空调气流等引起的作用于平台的压力，也能进行有效的隔离。因此本文选用混合控制隔振平台，即选择空气弹簧隔离高频振动，同时选用超磁致伸缩作动器隔离低频振动。

根据研究重点以及实验条件限制，本文主要研究竖直方向上相互耦合的三个自由度微振动控制，即竖直方向Z向，绕X轴转动θx和Y轴转动θy。三个作动器即可实现对该三个自由度的控制。因此该平台系统设计有一个平板，选用四个超磁致伸缩作动器，四个空气弹簧；四个空气弹簧分别放置在平板的四个角，四个超磁致伸缩作动器与空气弹簧竖向平行放置，如图1所示。

隔振平台系统中被动隔振组件采用西安弘力橡胶有限公司生产的工业用JBF75/106-2空气弹簧（不带附加气室），双曲囊形，上下层板为法兰密封。由于它所承受的荷载相对较小，所以气囊并不充气，让其依靠橡胶囊的弹性作用和气室间空气流动产生的阻尼来实现弹簧—阻尼模型。

超磁致伸缩材料在磁场中的尺寸会发生显著变形，可以通过控制驱动线圈产生的磁场来控制超磁致伸缩作动器的输出位移。与其它作动器相比,超磁致伸缩作动器具有性能稳定、漂移小、行程大、驱动力大等特点,适合于用作主动微振动控制系统的位移驱动器，主要用于隔离低频干扰。超磁致伸缩材料在外加磁场作用下，在磁化方向上产生伸长或缩短的特性，超磁致伸缩作动器利用其特性进行设计制作。随着大的超磁致伸缩应变，超磁致伸缩作动器的磁场输入和位移、应变输出具有较明显的磁滞非线性，这种非线性滞回性能影响超磁致伸缩作动器在振动控制中的控制及使用，所以有必要对作动器进行建模分析。

2 超磁致伸缩作动器的模拟

高精密仪器隔振平台系统的设计一般需要考虑各种复杂的微振动环境干扰[12]。这就要求设计的隔

在实际的动态控制应用当中，超磁致伸缩作动器的非线性滞回现象较为明显，因此对非线性进行补偿是必要的。

这种非线性主要是由磁场强度和磁化强度之间的磁滞特性引起的，因此在超磁致伸缩作动器分析模型中可以把这一环节进一步细化成磁滞和磁致伸缩两个部分，超磁致伸缩作动器结构分析模型如图2所示。

图2 超磁致伸缩作动器结构分析模型Fig.2 The analysis model for the giant magnetostrictive actuator

磁滞建模主要有两种方法：一种是以Preisach模型为代表的数学建模理论；另一种以Jiles-Atherton模型为代表的物理建模理论。由于Preisach模型是递归形式，其逆模型求解比较复杂[8]；而Jiles-Atherton模型是基于微磁学理论和Weiss分子场模型，通过磁化过程的能量守恒原理所导出的磁化过程中不可逆部分的表达式，从而得出外磁场和平均磁化强度的关系式。因此本文选用Jiles-Atherton模型。

Jiles-Atherton磁滞模型描述的是输入的磁场H和磁化强度M之间的关系。为建立磁滞模型，需要表示出有效磁场面积Heff与磁化强度M，非滞回磁化强度Man，不可逆磁化强度Mirr及可逆磁化强度Mrev的关系。

假设预压应力σ0不变，有效的磁场面积为Heff如式1。

式中H——外加激励磁场强度；αM(t)——磁化作用引起材料内部磁畴相互作用对于磁场强度的影响[13]。其中H=nI表示单位长度内缠绕圈导线的通电螺线管产生的磁场强度。

非滞回磁化强度模型选用Langevin模型，其磁化强度如式2和式3。

考虑能量耗散，不可逆磁化强度Mirr为

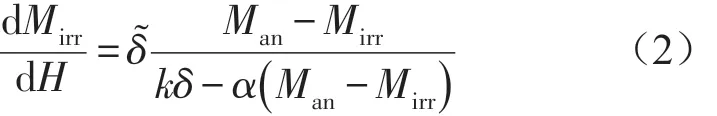
其中

可逆磁化强度Mrev为

总逆磁化强度M为

α、a、k、c、M s分别为畴壁相互作用系数、无磁滞磁化强度形状参数、不可逆损耗系数、可逆系数、饱和磁化强度。

作动器产生的都是正应变，为了得到双向应变，需要施加一直流电到螺线圈上，以提供偏置磁场（加权磁化强度2M(t)M s）。因此

其中M s为饱和磁化强度，λ s为饱和磁致伸缩应变，λ s的参数值取决于初始的磁畴方向，因此跟预压力作用相关[9]。

磁滞模型的逆补偿[14]可表示为公式6。

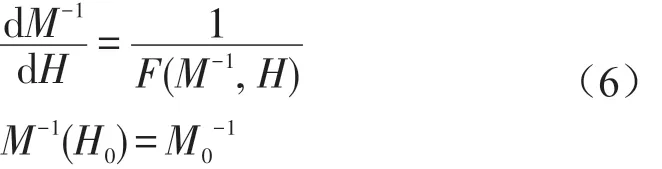
构造超磁致伸缩作动器全逆补偿模型及非线性作动器模型的过程如图3所示。

图3 超磁致伸缩作动器非线性模型及其全逆补偿原理图Fig.3 The diagram for the nonlinearity of the giant magnetostrictive actuator and full inverse compensation

针对超磁致伸缩作动器非线性及其全逆磁滞补偿建立了数值仿真模型。用于仿真的超磁致伸缩作动器的参数来自于文献[15]的实验参数如表1所示。

表1 作动器的参数[15]Tab.1 Parameters for an experimental actuator

假定作动器的目标控制力如式7所示。

将目标控制力输入逆补偿模型对作动器的非线性进行补偿，所得电流值输入作动器模型中，作动器产生的输出控制力与输入的目标控制力对比分析如图4所示。

图4 输入的控制力和输出控制力的比较Fig.4 The comparison between the input control force and the output control force

由图4可知，所建立的逆补偿数值仿真模型是可行的、有效的，从而使得该作动器可以有效的控制结构的振动。为进一步将作动器模型植入多自由度微振动混合控制系统的研究打下基础。

3 基于超磁致伸缩作动器模型的混合控制系统仿真

本文研究竖向相互耦合的的三个自由度即竖直Z向，绕X轴转动和绕Y轴转动，依据本文的平台设计将四个作动器模型及其逆补偿模型植入该微振动控制系统进行控制研究，其仿真流程图如图5所示。

图5 基于作动器模型的控制系统流程图Fig.5 Flowchart of based on actuator model control system

根据文献[12]，选用白噪声作为来自地面的水平干扰输入结构的底部，用MATLAB程序实现干扰信号的生成。

选用LQG控制算法对多自由度微振动平台进行控制。状态方程如式8所示

式中[M]——质量矩阵；[K]——刚度矩阵；[C]——阻尼矩阵；[Ka]——控制力输出因子矩阵。状态向量其中

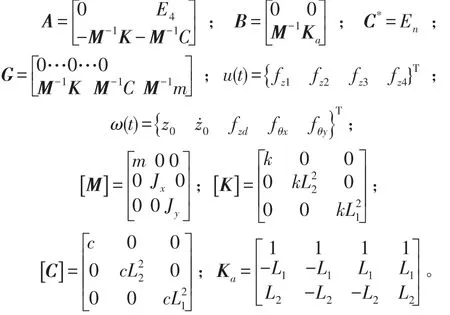
式中fzi(i=1，2，3，4)是指放置在平台四个脚落处作动器的出力；i=d是指沿Z方向的直接干扰力；fθx和fθy是指沿X轴，Y轴转动的直接干扰力；z0是基础干扰；k是指刚度，c是指阻尼，Li参见图1标注所示。MATLAB环境中建立微振动平台隔振系统，选用LQG算法对其进行控制，经过多次试选，取加权矩阵

考虑实际可行性，量测作动器所在四个位置的位移作为观测信号进行反馈，通过整体坐标与局部坐标之间的变换，得到整体坐标Z方向的位移以及绕X轴转动的θx和绕Y轴转动θy；同时也对该系统进行了被动控制研究，被动控制考虑仅在空气弹簧作用下平台板的响应。将基于作动器模型的混合控制仿真结果同被动控制仿真结果进行对比，仿真数值结果如表2和表3所示。

从位移和速度的峰值和均方根值对比结果可以看出，混合控制从三个方向上都取得了较好的控制效果，且位移控制效果更加明显。对比分析两者竖直方向三个自由度的位移结果可知：混合控制下Z方向的位移和速度均方根值分别为被动控制的27.31%和28.62%；θx方向的角位移和速度均方根值分别为被动控制的0.966 8%和17.19%；θy方向的角位移和速度均方根值分别为被动控制的1.219%和41.85%。可以看出，基于作动器模型的混合控制方案可以进一步有效隔离环境干扰。

表2 位移控制结果对比Tab.2 The comparison of the displacement control results

表3 速度控制结果对比Tab.3 The comparison of the velocity control results

4 结语

超磁致伸缩作动器的非线性特性对多自由度平台微振动控制系统产生的制约作用，造成了理论与实验结果会有较大的差别。为了更好的服务于实际工程，将超磁致伸缩作动器非线性及其逆补偿模型植入混合控制系统，利用最优控制理论，对多自由度微振动混合控制隔振平台进行数值仿真研究。

结果表明，混合控制下Z方向的位移和速度均方根值分别为被动控制的27.31%和28.62%；θx方向的角位移和速度均方根值分别为被动控制的0.966 8%和17.19%；θy方向的角位移均方根值分别为被动控制的1.219%和41.85%。由此可见，基于作动器模型的混合控制方案可以进一步有效隔离环境干扰，且由于更贴近于实际情况，为隔振平台系统用于实际工程提供了可靠的理论依据。

[1]Gardonio P,Elliott S J,Pinnington R J.Active isolation of structural vibration on a multiple degree of freedom system,Part I:The dynamics of the system[J].Journal of Sound and Vibration,1997,207(1):61-93.

[2]刘红军，刘 洁，程 江.双向解耦平台与结构一体化的混合控制分析[J].振动工程学报，2012，25(2)：174-180.

[3]郝慧荣，白鸿柏，张慧杰.六自由度主被动一体隔振平台鲁棒控制[J].振动与冲击，2012，31(7)：122-127.

[4]Hale M.T.and Porter J.F.Validation techniques for 6-DOF vibration data acquisition[J].Journal of the IEST.,2012,55(1):10-24.

[5]Davliakos I.and Papadopoulos E.Model-based control of a 6-DOF electrohydraulic Stewart-Gough platform[J].Mechanism and Machine Theory,2008,43(11):1385-1400.

[6]关广丰，王海涛，熊 伟，韩俊伟.6自由度液压振动台运动学分析及控制策略[J].振动、测试与诊断，2011，31(001)：89-93.

[7]Fujita T,Tagawa Y,Kajiwara K,Yoshioka H,Takeshita A,and Yasuda M.Active 6-DOF microvibration control system using piezoelectric actuator[A].Proceedings of the third conference on adaptive structures[C].San Diego,California:Technomic Publishign Co.,Inc.1992.514-528.

[8]Nakamura Y,Nakayama M,Kura M,Yasuda M,Fujita T.Application of active micro-vibration control system using a giant magnetostrictive actuator[J].Intelligent Material Systems and Structures,2007,18(11):1137-1148.

[9]张春良.微制造平台振动主动控制研究[D].杭州：浙江大学，2003.

[10]Y.L.Xu and B.Li.Hybrid platform for high-tech equipment protection against earthquake and microvibration[J].Earthquake Engineering ＆ Structural Dynamics,,2006,35:943-967.

[11]陶 帅，等.基于压电致动器的微动隔振平台系统[J].振动与冲击，2010，29(003)：147-149.

[12]Ungar E E,Sturz D H,Amick C H.Vibration control design of high-technology facilities[J].Sound and Vibrattiioonn,,1990,24(7):20-27.

[13]卢全国，陈定方，陈 昆.基于Preisach修正模型的GMA前馈补偿研究[J].武汉理工大学学报，2007，29(1)：48-51.

[14]韩同鹏，李国平.基于磁化机理的超磁致伸缩执行器磁滞模型[J].功能材料与器件学报，2010，16(1)：41-46.

[15]Smith R C.Inverse compensation for hysteresis in magnetostrictive transducers[J]. Mathematical and Computer Modeling,2001,33:285-298.