基于改进型滑动窗主元分析的盾构液压系统故障诊断研究

周奇才 黄 克 赵 炯 熊肖磊

同济大学，上海，201804

0 引言

统计过程监控（statistical process monitoring，SPM）是在工业流程生产领域广泛应用的故障诊断技术，可有效提高流程品质和生产率。其中，主 元 分 析 （principal component analysis，PCA）是最常见的一种SPM技术。PCA的特点是丢弃噪声和过程变量间共线性关系，保存原始数据集最重要的信息，其基本流程如下：首先在正常过程状态采集数据建立PCA模型，然后计算监控统计量的控制限，最后根据这些统计量对生产过程进行在线监控［1］。目前，PCA在故障诊断、信号处理和模式识别等领域都有不同程度的应用［2］。

液压驱动是盾构机的主要驱动方式，刀盘旋转和推进系统均依赖液压系统传递动力，所以液压系统是关键系统，也是故障检测重点。现有盾构机液压系统故障检测采用单传感器检测、人工判断方式，但液压系统故障发生成因具有多样性，故障发生时若只考虑某一元件的故障而忽略其他元件运行情况的话，诊断结果是不准确的。

贺湘宇［3］将动态PCA应用于挖掘机液压系统故障诊断，实现了液压泵、阀、液压缸堵塞和磨损引发故障的辨识。但是液压系统运行过程具有时变性，随着系统运行的持续，系统及传感器的固有参数也在发生变化，因此，PCA模型需要自适应更新。Jeng［4］指出，对于时变系统采用移动窗更新模型的方式更加合适。Wang等［5］提出了快速移动窗PCA的整体架构以及相关矩阵的递推更新算法，但没有给出更详细的算法。

根据液压系统的时变、动态特性，本文提出了滑动窗算法和动态PCA相结合的算法，并将其应用于盾构液压系统故障诊断中。

1 盾构液压系统的PCA分块

盾构机是机、电、液技术高度集成的工程机械，含有大量机械、液压和电气装置，因此，在建立统计过程模型时，对模型中各变量之间相互关系的解释极为复杂，使模型难以获得实际应用。一种有效的办法就是建立分层（hierarchical）模型或分块（multi-block）模型，将整个装置分为若干子系统，对每一子系统建立相应的模型。由于模型中的测量变量都是来自于同一过程单元（或者同一子系统），变量之间的相互关系相对比较明确，模型的解释能力比较强［6］。Wold等［7］分别阐述了分块PCA和PLS（partical least square）思想（它们能够使监控模型的解释能力得到增强）。

盾构机是一类主要靠液压驱动的大型工程机械，可完成盾构刀盘旋转、推进、拼装机旋转等动作。将PCA分块思想按照上述动作进行划分，如图1所示。

图1 盾构机分块示意图

由图1可知，盾构液压系统可以看作由刀盘旋转子系统、推进子系统、拼装机子系统、螺旋输送子系统等多个子液压系统组成的复杂液压系统。对每一个子系统按照功能细分，又可分为能源装置（各种规格泵）、控制装置（三位四通电磁换向阀、溢流阀等）、执行装置（完成各项动作的液压缸）。虽然盾构液压系统包含众多子系统，可完成盾构机地下挖掘多种动作，但是按照功能划分又有相似之处，由此可以研究基本液压系统的故障诊断，然后推广到各个子系统中。根据盾构液压系统总结出基本液压系统，包括泵、换向阀、溢流阀和液压缸。

2 改进型PCA算法

改进型PCA算法将简单的移动窗过滤的基本原理与PCA相结合，其基本步骤如下：

（1）用历史数据构建PCA模型，并确定各种统计参数，标准化PCA。

（2）对未超过统计控制限的新数据纳入PCA模型中，并将旧数据删除，基于新模型更新各统计参数。

何小斌［8］提出了自适应移动窗算法（移动窗长度随着更新数据变化而自适应）。Liu等［9］提出了更有效的、节约内存的移动窗算法。然而移动窗构建算法中无论PCA模型还是更新算法均没有考虑数据序列相关性。本文将动态PCA算法与移动窗算法相结合，并更新计算公式。

一个完整的移动窗算法需要考虑：①递归更新样本均值、方差和协方差矩阵；②具有一种更新特征空间的递归算法；③更新各监控指标的置信限。

2.1 更新协方差矩阵

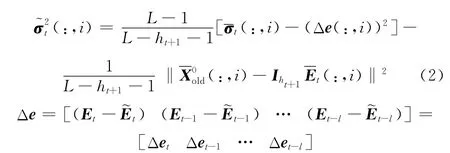
由式（4）可以推导出矩阵Ⅱ的协方差矩阵：

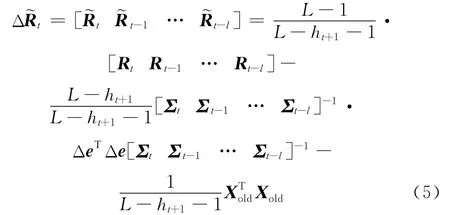
2.2 特征值更新

令

则

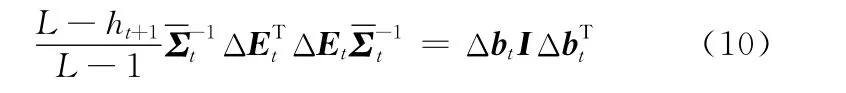
综合式（9）～式（11），将式（7）改写为

令变量B、C分别为

则

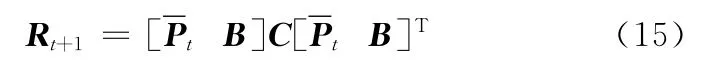
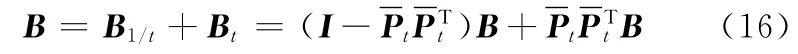
为了使B1／t正交，对其进行QR分解，即

由式（16）、式（17）可得

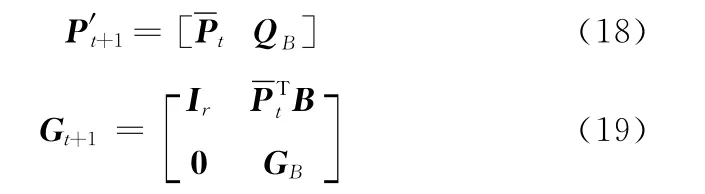
整理以上各式可得

对式（20）中间项奇异值分解：

联立式（20）、式（21）可得

即

2.3 监控统计量更新

由于系统PCA模型得到更新，那么统计量和其控制限也需要自适应更新。PCA将测量空间分成主元空间和残差空间，统计量T2（Hotelling T2检验）和SPE（squared prediction error，SPE）或Q分别描述对应空间的变化。

Hotelling T2统计量为

同理也可以获得矩阵Ⅲ的两个统计量。统计量的监控限公式可以参考相关文献，此处不再累述。

3 系统仿真及故障识别

3.1 系统仿真建模

由上文分析可知，虽然盾构液压系统由众多子系统组成，异常复杂，但是各子系统有以下共性：共用油箱，均由各自泵、功能阀块和执行液压缸组成。如拼装机液压系统，实现垂直、上下、左右三个方向的动作，三种动作共用一个液压泵，以及各自的功能阀块和执行液压缸（组），其中功能阀块主要包括换向阀、双单向节流阀和泄荷阀。取左右方向动作的液压子系统为仿真对象，采用AMESIM软件［11］建立仿真液压系统图（图2），由于各阀块跟数学模型相关联，因此，通过修改数学模型模拟仿真液压系统发生的故障。

图2 拼装机左右动作液压子系统

3.2 故障仿真

由于地下环境的复杂性，盾构机挖掘工况具有时变性，数据采集样本的均值、协方差甚至主元数目等统计量处于变化状态，因此，用静态PCA模型去监测系统故障情况时必然导致较高的误报率。

根据上海地铁盾构设备工程有限公司提供的历史故障记录统计：液压设备损坏故障较少发生；由磨损造成的泵容积效率下降，由密封圈老化、油液污染、装配精度等原因造成的泄漏，油液颗粒污染造成的堵塞，这几种故障最为常见。

由图2可知，该子系统的关键部件是泵、换向阀和执行液压缸。通过设定柱塞泵的柱塞与缸体直径间隙仿真磨损或泄漏F1，设定换向阀阀芯的间隙直径仿真换向阀磨损F2、阀芯的流量系数仿真换向阀堵塞故障F3，设定液压缸的泄漏系数仿真泄漏故障F4，输入变量取泵的输出流量Q1和压力p1，换向阀的输出流量Q2和压力p2，液压缸（有杆腔）的输出流量Q3和压力p3，并令动态PCA的时滞参数l＝2。

为了验证改进型滑动窗算法的有效性，引入两个过程缓慢漂移，正常过程下采集700组数据，将300组Q1和Q3（随机的）加上正漂移0.07，将后400组数据加上负漂移0.06，以便形成幅值为0.01的正漂移。

对采集样本数据计算主元贡献率和累积贡献率，见表1（取前6个）。

表1 主元贡献率和累积贡献率 %

若主元累积贡献率大于85%，则取第1主元即可满足要求。在采集样本的基础上加入缓慢漂移，并用本文的改进型移动窗算法更新PCA模型。共获得18个主元，其单个贡献率和累积贡献率见表2（有省略）。

表2 更新模型主元贡献率和累积贡献率 %

由表2可知，加入缓慢漂移后系统PCA模型主元空间和残差空间均发生变化，可见改进型算法能适应当前系统的变化。分别令置信水平α＝0.05和α＝0.01。更新模型前后的统计量T2和Q见图3、图4。

图3 更新模型前两统计量和控制限

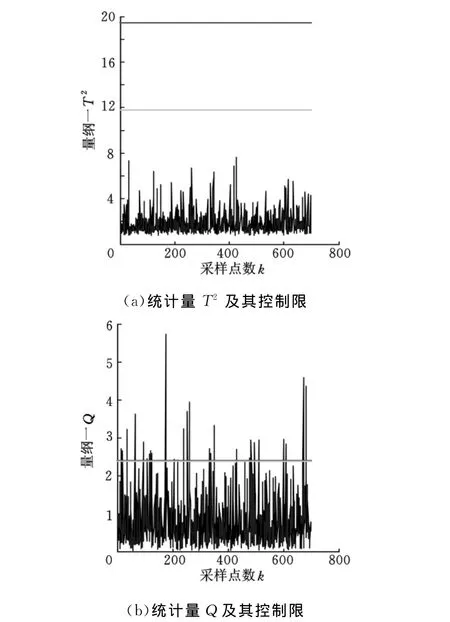
图4 更新模型后两统计量和控制限

从图4可知，加入缓慢漂移后由于PCA模型获得更新，两统计监控量能起到有效监控作用，而从图3可知，对原本属于系统设备老化、传感器漂移等因素引起的样本均值、方差甚至协方差矩阵等统计量的变化，更新前PCA模型发出了报警信息，因此，该模型对时变系统的监测误差较大。

实验共测试4种故障形式，故障描述以及涉及的参数见表3［3］。

表3 故障描述

限于篇幅，只针对F4故障加以详细说明，其余故障分析类似。拼装机液压系统液压缸属于柱塞式液压缸，液压缸泄漏分为内泄和外泄，外泄可通过观察液压缸表面是否有油液泄出获知；内泄由于发生在液压缸内部，不易观察，所以这里主要分析该类故障。令活塞磨损造成液压缸泄漏增加，在AMESIM 中设置液压缸泄漏系数（将0.001改为0.05）。分三个时刻各采集700组数据（作为输入矩阵样本），利用已经更新完毕的PCA模型对样本分析，统计量见图5，不论T2还是Q统计量均发现故障。

图5 F4液压缸泄漏故障PCA分析

统计量能发现故障，却无法确定故障源，而贡献图能显示某时刻单变量波动情况，第j个变量在i时刻的SPE的统计量的贡献Qi，j可按照如下公式计算：

液压缸泄漏的Qi，j见图6。由图6可知，液压缸油压和流量变化最大，应该是故障源，与分析基本吻合。

图6 F4故障SPE贡献图

4 结语

本文提出了基于滑动窗算法和动态PCA相结合的算法，该算法能自适应更新PCA模型，有效提高诊断准确度，减少误判的发生。盾构液压系统是盾构机主要组成部分，也是故障诊断的主要对象，以往故障诊断只针对单一液压元件来分析，而液压系统是一个统一的整体，各元件相互影响，因此，必须作为一个整体加以考虑。本文先对盾构液压系统分块，然后对每一子系统进行PCA分析，最后用仿真模拟加以验证，结果表明，该算法效果良好。

［1］Jackson J E.A User Guide to Principal Components［M］.New York：John-Wiley ＆ Sons Inc.，1991.

［2］Kresta J V，Macgregor J F.Multivariate Statistical Monitoring of Process Operating Performance［J］.Canadian Journal of Chemical Engineering，1991，69（1）：35-47.

［3］贺湘宇.挖掘机液压系统故障诊断方法研究［D］.长沙：中南大学，2008.

［4］Jeng J C.Adaptive Process Monitoring Using Efficient Recursive PCA and Moving Window PCA Algorithms［J］.Journal of the Taiwan Institute of Chemical Engineers，2010，41（4）：475-481.

［5］Wang X，Kruger U，Irwin G W.Process Monitoring Approach Using Fast Moving Window PCA［J］.Ind.Eng.Chem.Res.，2005，44（15）：5691-5702.

［6］MacGregor F，Jaeckle C，Kiparissides C，et al.Process Monitoring and Diagnosis by Multiblock PLS Methods［J］.AIChE.Journal，1994，40（5）：826-838.

［7］Wold S，Kettaneh N，Tjessem K.Hierarchical Multiblock PLS and PCA Models for Easier Interpretation and As An Alternative to Variable Selection［J］.Journal of Chemometrics，1996，10（5／6）：463-482.

［8］何小斌.基于统计学方法的自适应过程监控与故障诊断［D］.上海：上海交通大学，2008.

［9］Liu Xueqin，Kruger U，Littler T，et al.Moving Window Kernel PCA for Adaptive Monitoring of Nonlinear Processes［J］.Chemometrics and Intelligent Laboratory Systems，2009，96：132-143.

［10］Johnson R A，Wichern D W.实用多元统计分析［M］.6版.北京：清华大学出版社，2008.

［11］付永领，祁晓野.AMESIM系统建模和仿真.从入门到精通［J］.北京：北京航空航天大学出版社，2006.