基于行星传动调速的波浪补偿系统设计与样机研制

徐小军 陈 循 胡永攀

国防科学技术大学，长沙，410073

0 引言

在进行海上并靠补给吊装作业时，海浪的起伏会造成冲击和碰撞，给海上对驳吊装的效率和安全性带来不利影响。波浪补偿是指针对因水面起伏引起作业装备产生波动而进行的补偿校正。波浪补偿系统是波浪补偿功能具体实现的装备，它能使吊装作业不受水面波浪起伏的影响，从而增强海上作业的安全性、高效性和可靠性。波浪补偿系统具体结构形式多种多样，但按控制力的执行方式可分为被动式波浪补偿系统和主动式波浪补偿系统两种基本类型［1-2］。目前国内已经开发了几种被动式波浪补偿系统并成功应用于海上并靠补给作业。相对于主动式波浪补偿系统，被动式波浪补偿系统存在补偿范围受补偿设备行程的限制，补偿负载受储能装置压力的限制，且需要配备额外体积庞大的辅助装置等问题［3］。国内针对主动式波浪补偿系统的研究主要处于实验和仿真阶段［4］。

本文提出的“基于行星传动的主动式波浪补偿系统”采用一种全新的补偿方式，利用行星传动机构的调速特性，将波浪补偿功能集成于吊装起重机上，将所有机械系统整合于一台行星传动调速器上，无需其他辅助装置，采用基于前馈补偿—反馈校正的波浪补偿复合控制方法实现主动式波浪补偿。

1 基于行星传动调速的波浪补偿系统工作原理

基于行星传动调速的主动式波浪补偿系统由控制系统、检测系统、电液伺服驱动系统和机械执行系统等四个子系统构成，如图1所示。

控制系统由硬件开发平台和软件系统构成，根据补给装置输入量、船舶姿态运动量和反馈量，通过一定的控制算法实现对电液伺服系统的控制。

检测系统由高性能传感器及数据处理单元构成，实现船舶姿态运动、绳索张力以及重物位移、速度等信号的实时检测。根据驱动控制量的不同，液压驱动系统分为主驱动电液伺服系统和副驱动电液伺服系统，分别输入主控信号（即补给装置输入量）和补偿信号。

图1 基于行星传动调速的主动式波浪补偿系统

机械执行系统则由行星传动调速卷扬机、离合制动器、绳索、滑轮组及起重架等组成，是实现物资补给的最终装置。

波浪补偿起重机需要实现平稳吊装作业功能，因此必须补偿由波浪引起的两船相对速度，该补偿速度的大小等于两船因波浪起伏引起的相对速度。基于行星传动调速的波浪补偿系统基本工作原理为：主驱动端的控制与普通液压起重机相同，副驱动端（实现绳索始终张紧的波浪补偿驱动端）用来实现波浪补偿功能；当两侧液压马达同向驱动时卷扬机转速增加，当两侧液压马达相互反向驱动时卷扬机转速降低；在正常工作状态下使用主驱动完成正常的升降工作，当海浪波动较大时，启动副驱动便形成波浪补偿系统，使得绳索始终处于张紧状态。具体工作过程如下：

（1）检测系统检测到两船舶姿态运动参数、起重绳索张力和重物运动参数，将数据传递给控制系统。

（2）控制系统根据补给速度参考信号、船舶姿态运动信号和反馈信号，经控制器运算后输出各种控制信号，分别控制主副驱动电液伺服系统。

（3）电液伺服系统根据控制信号决定比例阀的开口大小和方向，进而决定液压马达的转速和转向，机械执行系统通过行星传动调速器完成补给速度vS和补偿速度vC的合成运算，实现波浪补偿功能。

（4）检测系统不断将检测到的载荷以及船舶实际姿态运动参数、起重绳索张力等信息反馈给控制系统，控制系统根据误差和误差变化率的大小再计算出下一周期控制信号的大小，并将其传递给电液伺服系统，进行下一周期的控制。

2 基于前馈补偿—反馈校正的波浪补偿复合控制策略

主动式波浪补偿控制系统的目的是保证重物在波浪起伏的海况下从补给船平稳地吊装到被补给船上。所谓平稳，具体体现在两个方面：一是重物的绝对速度不出现急剧变化，起重绳索张力波动不大；二是重物起吊、着落时对甲板的冲击尽可能小。根据控制目的及行星传动调速波浪补偿系统的工作原理，控制系统设计的基本思路是：利用行星传动调速器进行主控信号和补偿信号的分开处理与复合控制，实现波浪补偿；利用高性能DSP控制器实现控制算法和数据处理［5］。以船舶相对运动信号作为前馈补偿信号，以重物相对被补给船的速度、位移和起重绳索绳张力信号作为反馈校正信号，实现控制系统前馈补偿—反馈校正的复合控制。

图2所示的控制结构框图表示波浪补偿控制系统方案。其中，R（z）为补给船吊钩的理想运动曲线；Gm1（z）为主驱动部分（电液伺服驱动系统和差动行星轮主传动部分）的传递函数；Gm2（z）为副驱动部分（电液伺服驱动系统和差动行星轮副传动部分）的传递函数；Gw（z）为卷扬机的传递函数；Gs2（z）为卷扬机到滑轮之间（绳索和滑轮）的传递函数；Gs1（z）为滑轮到重物之间（绳索和重物）的传递函数；L（z）为重物的状态；C（z）为补给船和被补给船的相对运动姿态；HPID（z）和 HVMP（z）为所要设计的控制器；T（z）为载荷产生的扭矩；M为载荷质量。

2.1 反馈控制策略

图3为反馈控制传递函数框图。其中，Rv（z）为rv（t）的Z变换（余同），rv（t）为控制系统参考输入量，为给定的补给速度，由其产生的闭环输出响应yv（t）为重物的实际补给速度；T为绳索张力；N（z）为张力变化值；控制器H的作用一是实现给定补给速度rv（t）的跟踪控制，二是把绳索张力T作为一个反馈控制的辅助手段，从绳索张力T中剔除由于补给船加速度的变化导致的张力变化部分（设为Te），通过修正给定的补给速度rv（t），使得重物在下降过程中绳索张力T的变化幅度控制在一定的范围内，并且重物与甲板接触时Te不发生急剧的下降，从而避免对被补给船形成冲击。

图2 控制结构框图

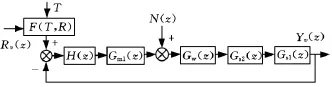
图3 反馈控制子系统

反馈控制系统的闭环输出传递函数为

2.2 前馈控制策略

主动式波浪补偿控制系统的目的是要补偿由波浪造成的重物与被补给船之间的相对运动速度，使重物按照给定的补给速度向被补给船甲板降落。要达到这个目的，必须获得补给船和被补给船之间的相对运动姿态c（t），由c（t）产生的系统输出响应为yc（t），系统的前馈控制框图见图4。

图4 前馈控制子系统

由图4所示的控制框图可得前馈控制传递函数为

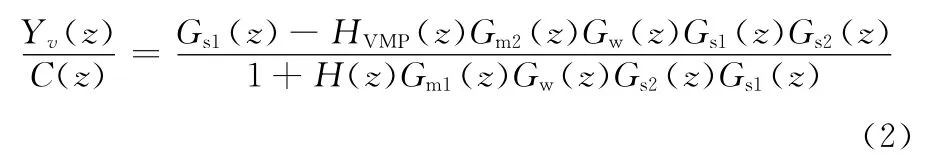
前馈控制的目的是使船舶姿态相对运动量c（t）所导致的系统输出yv（t）为零，从而使得货物能够在反馈控制器的作用下不受波浪的干扰，相对被补给船匀速下落。也就是说，在前馈控制器的作用下，使得前馈传递函数Yv（z）／C（z）＝0。

3 波浪补偿数学模型

3.1 液压马达

液压马达转速的计算公式为

式中，n为液压马达的转速；q为液压系统的流量；Vm为液压马达的排量。

实际工程中，考虑液压马达确定后其排量Vm便唯一确定，得知液压马达的转速n为输入流量q的一元函数关系式，可将式（3）改写为

流量q由伺服阀的输入电流和系统压力决定，流量方程为

式中，I为伺服阀的输入电流；pf为系统压力，对特定的波浪补偿系统，为保持液压系统工作的稳定性，通常设定为一具体恒定值；KQ、Kc分别为与系统结构有关的系数。

式（5）实际为因变量q和自变量I的一元关系式，可改写为

3.2 行星传动调速器

如图5所示，图中，a为太阳轮，b为内齿圈，g为行星轮，H为行星架。假设行星传动调速器输入转速为na、nb，输出转速为nw，则理想输入输出关系为

式中，za、zb分别为太阳轮a与内齿圈b的齿数；Rw为卷扬机滚筒半径；vw为输出线速度，即绳索始端速度。

图5 行星传动调速器差动传动原理

3.3 波浪补偿变量传递关系

由检测系统可得到以下变量：绳索张力变动量ΔT，被补给船与补给船之间的相对升沉运动速度变动量Δυ，绳索末端重物升降速度变动量Δvw。

按（ΔT，Δυ，Δvw）确定的三维向量考虑，则存在传感器输出信号量ξ，使得

式中，ξ为传感器输出信号量矩阵；Fξ为传感器组的特征变换函数结构矩阵。

已知检测信号量（ΔT，Δυ，Δvw）、补偿期望目标值（υs，Ts）（即设定误差），可由控制系统求解器得到确定的控制量矩阵 —— 向量值（I，q，n，…），写成结构关系式即为

式中，I为电液伺服系统的控制电流向量；FDSP为DSP特征变换函数结构矩阵；υs为速度补偿期望值；Ts为张力补偿期望值。

因此，波浪补偿系统在一次信号调制过程中的变量传递关系表现为以下过程：

波浪补偿系统按式（10）完成一个循环的信号调制、变量传递，实现一个周期的波浪补偿，如此反复循环。联立式（3）、式（6）、式（9），整理即得到波浪补偿系统变量特征传递关系：

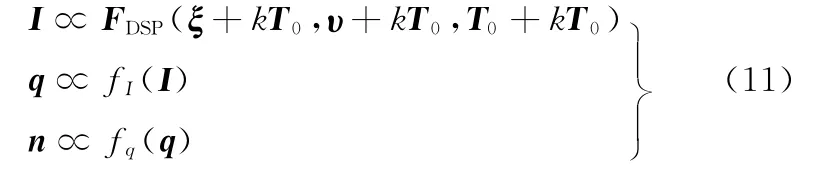
式中，T0为循环周期时间长度；k为循环周期数量。

4 行星传动调速波浪补偿样机

4.1 行星传动调速器

原型试验样机所用行星传动调速器基本齿轮参数如下：模数m＝2，齿形压力角α＝20°，行星轮齿数zg＝29，太阳轮齿数za＝19，内齿圈齿数zb＝77。设计绳索滚筒直径为164mm，滚筒宽度为65mm，行星架回转直径为48mm。其余结构件尺寸设计以上述参数为基础，充分考虑连接、承载能力特性要求等条件，设计并试制的行星传动调速器如图6所示。

图6 行星传动调速器实物图

4.2 电液伺服驱动系统

基于行星传动调速的主动式波浪补偿液压驱动系统控制回路如图7所示，它主要实现起重和补偿两个动作的功能控制。其中波浪补偿回路是最重要的，其本质是一个电液伺服系统，基本参数如下：系统压力6.3MPa，马达转速0～160r／min，马达输出扭矩50N·m，稳态精度不超过5%，响应时间不超过0.4s。

图7 液压系统原理图

4.3 船舶姿态检测系统

基于行星传动调速的波浪补偿检测系统组成如图8所示。检测系统主要完成两方面的信号检测：

（1）船舶运动姿态信号检测。补给船A和被补给船B分别安装加速度传感器，检测各自的升沉和纵摇运动状态。

（2）补给装置反馈信号检测。反馈信号包括重物相对于被补给船的速度信号、绳索张力信号。

图8 波浪补偿检测系统

5 试验验证

如图9所示，基于行星传动调速的波浪补偿原型样机试验系统由行星传动调速卷扬机、船舶姿态模拟平台、DSP控制器、液压马达和传感器等组成。

图9 波浪补偿原型样机试验系统

船舶姿态模拟平台要求能够实现升沉和倾斜两个自由度的运动，用来模拟甲板的升沉和纵倾。升沉运动采用正弦机构（曲柄滑块机构）来实现，倾斜运动采用凸轮机构实现。升沉为正弦运动，幅值为±0.6m，周期为5～10s；倾斜角度为0～5°，周期为5～10s。

5.1 动态特性试验

动态特性试验的目的是通过在“理想状态”下测试原型样机对阶跃信号和正弦信号的响应，得到原型样机的响应时间、稳态误差等动态特性参数，从而验证电液伺服系统的控制原理和控制算法的正确性。其中“理想状态”是指：假设调速器无传动误差，波浪起伏引起的船舶相对运动速度为理想状态下的阶跃输入和正弦输入。

（1）对阶跃信号的响应。使用信号发生器给伺服阀输入一个阶跃信号，通过旋转编码器测量行星传动调速器两输入端的转速，得到原型样机对阶跃信号的响应，如图10a所示。可以看出，主动式波浪补偿系统对阶跃信号的响应曲线是无超调的，响应时间约为0.5s，稳态误差小，满足设计指标要求。

（2）对正弦信号的跟随。使用信号发生器在伺服阀的输入端输入一个正弦信号，通过旋转编码器测量行星传动调速器两输入端的转速，得到原型样机对正弦信号的跟随情况，如图10b所示，可以看出，液压伺服系统对正弦输入信号的响应较好，跟踪时滞约为0.2s，满足设计指标要求。

图10 原型样机对阶跃信号与正弦信号的响应

（3）正弦信号输入下绳索张力变化。使用信号发生器在伺服阀的输入端输入一个正弦信号，通过张力传感器测量绳索的张力，得到绳索张力对正弦信号的跟随情况，如图11所示，可以看出，张力在一定范围内波动，绳索始终保持在张紧状态。此外试验还表明，绳索张力的变化除了与系统动态特性有关外，还与绳索的材料等属性有关。

图11 绳索张力对正弦信号的响应

5.2 波浪补偿试验

为了验证波浪补偿效果，通过原型样机试验系统进行了多种条件下的波浪补偿试验。

设计波浪补偿系统作业过程的补给速度曲线，分为加速启动、稳定运行和减速制动过程。其中，匀加速启动时间1s，减速制动时间0.1s，稳定运行速度为0.5m／s，如图12所示。图13所示为波浪补偿系统运行全过程的试验结果曲线，运动干扰信号频率为0.2Hz。 在 不 同 频 率（低频f＝0.05Hz，高频f＝2Hz）的船舶运动情况下进行了波浪补偿系统稳定运行试验。

图12 补给作业速度参考曲线

图13 原型样机波浪补偿曲线

5.3 试验结果分析

在试验过程中，采用了图12所示的补给速度控制曲线。考虑补偿系统对快速制动要求很高，因此曲线的速度下降部分变化很快。图13表明波浪补偿系统的启停控制效果良好，响应时间为0.18s，速度稳态误差仅1.5%，张力稳态误差仅为1%，完全符合原型样机技术指标要求。

从图14和图15可以看出，补偿系统在稳定运行过程中，船舶运动信号对补偿效果和系统控制性能影响很大。在低频条件下，系统能高精度地补偿船舶运动干扰，而在高频条件下重物呈现微幅振荡，绳索张力也变化频繁，此时系统的补偿精度降低。在高频f＝2Hz的情况下，速度误差范围小于10%，绳索张力变化范围小于7.5%，因此仍然符合设计要求。

在真实海况下，船舶的运动频率偏低，因此对整个系统而言，波浪补偿效果比较满意，试验结果基本能够满足波浪补偿系统控制需要。

6 结论

（1）本文设计的基于行星传动的波浪补偿系统能及时跟随模拟波浪的运动变化。

图14 船舶低频运动干扰结果

图15 船舶高频运动干扰结果

（2）原型样机在波浪补偿的过程中，绳索始终有张力存在，绳索不会出现松弛现象。

（3）按照本文提出的设计理论和分析方法建立的基于行星传动调速的波浪补偿系统基本满足复杂海况条件下吊装作业的要求。

［1］Drevdal K E.Active Heave Drilling TM-a New Standard in Heave Compensation Technology［S］.HITEC，2001.

［2］Sagatun S I，Johansen T A.Wave Synchronizing Crane Control during Water Entry in Offshore Moonpool Operations-Experimental Results［J］.IEEE Journal of Oceanic Engineering，2003，28（4）：720-728.

［3］Otani A，Yoshitomi T.Vertical Seismic Response of Overhead Crane［J］.Nuclear Engineering and Design，2002，212（1／3）：211-220.

［4］贺可太.海上波浪补偿起重机控制研究［D］.北京：北京航空航天大学，2000.

［5］徐小军，何平，陈循，等.基于DSP的主动式波浪补偿起重机控制系统设计［J］.国防科技大学学报，2008，30（1）：110-114.Xu Xiaojun，He Ping，Chen Xun，et al.Design of Control System for an Active Heave Compensation Crane with DSP［J］.Journal of National University of Denfense Techonogy，2008，30（1）：110-114.