一种医学图像局部结构的尺度选择方法

【作 者】沈庄明，秦斌杰

上海交通大学生物医学工程学院，上海市，200240

0 介绍

图像内局部结构的尺度信息是图像处理中一个重要的参数。在医学图像处理领域，为血管、肺结节等局部结构选择适合它们的尺度，对进一步处理、分析这些图像有至关重要的作用。例如，在计算机辅助的肺部诊断中，对肺结节进行分割是一项极为有意义的工作，而合理地估计出肺结节区域的尺度大小将有助于分割这些病灶区域[1]。除了图像分割上的应用外，在去除医学图像中的噪声信号时也常常需要对尺度进行估计。例如，利用小波将超声图像分解为细节部分后，通过估计图像内细节部分（噪声）的方差（尺度），可以达到图像去噪的目的[2]。

然而，据我们了解，除了Narayanan等[3]估计待配准图像中未匹配区域的尺度信息，Hahn等[4]在配准多模图像时，提出自适应地选取各向异性核函数的尺度外，大多数的研究者尚未对图像配准中局部结构尺度的计算给予足够关注。这也促使我们在本文中提出一种适用于医学图像局部结构尺度估计的方法，以满足后续医学图像配准中对局部结构尺度信息的需求。

总体上说，我们可以通过两大类的方法[5]为图像中的局部结构选择合适的尺度，即插入法（plug-in method）和拟合法（goodness-of-fit method）。插入法在实际信号与估计信号的均方差达到最小时，通过对信号偏差与方差的估计来计算信号的尺度[6-7]。相对而言，拟合法并不估计信号的偏差和方差，而是在交叉验证（cross-validation）、赤池信息量准则（Akaik information criterion,AIC）等最佳精度准则的条件下选取最优尺度[8-9]。由于拟合法是一种数据驱动的方法，因此其在使用时更加灵活。本文将利用这一特点，提出了一种适用于多分辨率医学图像配准的局部结构尺度选择方法。

1 原理与方法

局部结构尺度选择流程如图1所示。首先，我们利用简单线性迭代聚类算法(Simple Linear Iterative Clustering,SLIC)[10]将图像I(x)划分为不同的小结构区域，即超像素(superpixels)。由于这些小结构区域保留了图像中显著结构的边缘，因此可将它们视为对图像局部显著结构的一种表达。我们记图像区域为φ，局部结构为Si，i=1,...n显然有φ=∪i=1Si。图n2和图3分别展示了多分辨率框架下，利用简单线性迭代聚类算法对血管图像和视网膜图像进行分割后得到的局部结构(超像素)。

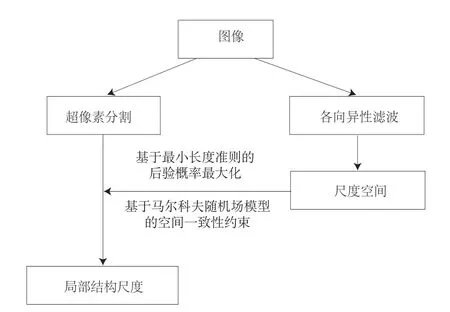
图1 算法流程Fig.1 Flowchart of algorithm

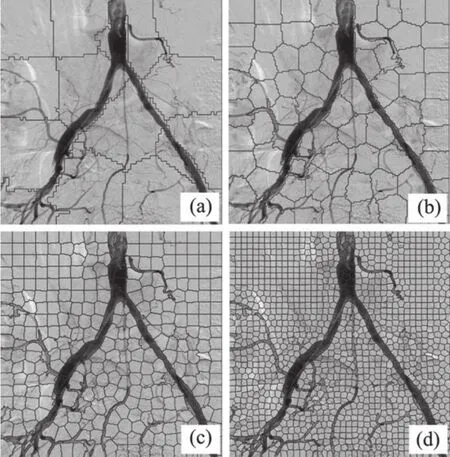
图2 血管图像的多分辨率超像素分割(a)～(d)图像分辨率分别为80×82、161×165、322×330和644×660像素时的超像素分割图Fig.2 Superpixels in multi-resolution vascular images(a)～(d)Superpixels at the 80×82,161×165,322×330 and 644×660 pixel resolutions

图3 视网膜图像的多分辨率超像素分割(a)～(d)图像分辨率分别为50×31、100×62、200×124和400×248像素时的超像素分割图Fig.3 Superpixels in multi-resolution retina images(a)～(d)Superpixels at the 50×31,100×62,200×124 and 400×248 pixel resolutions

在对图像进行局部结构划分的同时，我们还利用各向异性扩散方程[11]对图像I(x)进行光滑，以此构建图像的离散尺度空间。

由于最小描述长度准则[12]假定光滑项Iσk(Si)的描述长度与成反比，而残差项εσk的描述长度与成正比，因此，我们可以通过公式（3）对p(x│σk)进行估计[6]：

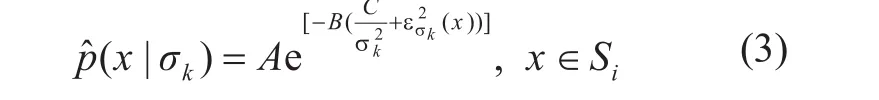
其中A为归一化常数，B ＞ 0和C ＞ 0是用于调节光滑项和残差项对公式（3）作用的经验参数，在本文中它们都被设置为1。

考虑到相邻局部结构间存在尺度相关性，将马尔科夫随机场（Markov random field,MRF）模型也纳入到局部结构尺度的选择中[6][7]。这里的马尔科夫随机场模型是通过图（graph）G=(v,ε)定义的，其中v={v1,v2,...,vn}表示图上顶点（vertex）的集合，ε为连接这些顶点的边（edge）的集合。在本文中，图像I(x)上的局部结构Si被抽象为这里的顶点vi，1≤i≤n。引入马尔科夫随机场模型后，就可以通过公式(4)对图像中局部结构的尺度进行选择。

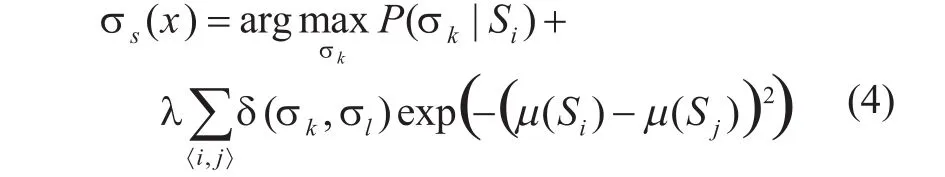
2 实验结果及讨论

通过两个医学图像的实例，展示我们尺度估计的结果，以不同灰度等级表示不同的尺度大小(最小尺度为1时，分配最暗的灰度，最大尺度为15时，分配最亮的灰度)。目前我们仅通过目测不同分辨率下的尺度估计效果来印证尺度估计的合理性。

图4 血管数字减影图像的局部结构尺度(a)原始图像，(b)～(e)图像分辨率分别为80×82、161×165、322×330和644×660像素时的尺度图Fig.4 Multi-resolution local structure scales of vascular DSA(a)Origin image,(b)～(e)Scale maps at the 80×82,161×165,322×330 and 644×660 pixel resolutions.

第一组实验是为一幅血管数字减影图像（digital subtraction angiography,DSA）中局部结构选择尺度（如图4所示）。在这幅血管的减影图（图4(a)）中，不同粗细的血管构成了图像中具有不同尺度的局部结构。图4(b)～(e)展示了不同图像分辨率下计算得到的尺度图。在这些尺度图中，灰度较暗区域被赋予尺度条中较小的尺度值，它们对应于图4(a)中的小尺度结构（如较细的血管），而尺度图中灰度较亮区域则分配到尺度条中较大的尺度值，它们对应于图4(a)中较为光滑的区域。在低分辨率下，由于超像素局部区域划分得较大，因此图像中一些较细的血管并不可区分，它们只能被赋予与周围区域一致的较大尺度值而呈现较亮的灰度（图4(c)）。随着图像分辨的提高，这些较细的血管逐步被分配较小的尺度值而显示更暗的灰度（图4(b)～(e)）。相对地，低分辨率下可被识别的粗血管，则逐步被赋予尺度条中较大的尺度值而展现出更亮的灰度。

第二组实验对视网膜图像中的局部结构尺度进行计算，如图5所示。图5(a)中视网膜内的血管、视盘等构成了尺度大小不一的局部结构。图5(b)～(e)展示了不同图像分辨率下的尺度图。可以看出，在低分辨率下，局部结构的尺度分配较为单一，因此无法反映出图像内局部结构，特别是视网膜内血管的真正尺度（图5(b)）。随着图像分辨率的提高，超像素分块逐渐被细化，尺度图中尺度的变换也更丰富（图5(c)～(e)）。血管与周围区域逐步可分，并被赋予不同的灰度。到图像最高分辩时，尺度图（图5(e)）中血管区域灰度最暗，表明分配给它们的尺度最小，而视盘、背景等相对光滑的均质区域，则呈现出较亮的灰度，说明分配给它们的尺度比较大。

图5 视网膜图像的局部结构尺度(a)原始图像，(b)～(e)图像分辨率分别为50×31、100×62、200×124和400×248像素时的尺度图Fig.5 Multi-resolution local structure scales of retina image(a)Origin image,(b)～(e)Scale maps at the 50×31,100×62,200×124 and 400×248 pixel resolutions.

3 结论与展望

本文简要回顾了医学图像中尺度估计的应用，同时提出了一种数据驱动的局部结构尺度选择方法，以满足后续医学图像配准中对局部结构尺度信息的需求。实验结果初步表明了我们方法的合理性。

在后续的工作中，将对该方法计算得到的尺度做出更为详细的评价。此外，还会将该方法运用到我们基于联合显著图[13]和自适应核回归的非刚性图像配准[14]，通过将其与描述两幅图像间局部结构的未匹配尺度相结合，自动地调节核回归中核函数的局部尺度，用以控制参与浮动图像形变场重构的位移矢量采样量，实现局部结构匹配更加精确的非刚性医学图像配准。

[1]Okada K,Comaniciu D,Krishnan A.Robust anisotropic Gaussian fitting for volumetric characterization of pulmonary nodules in multislice CT[J].IEEE Trans Med Imag,2005,24(3): 409-423.

[2]Gupta S,Chauhan RC,Saxena SC.Locally adaptive wavelet domain Bayesian processor for denoising medical ultrasound images using Speckle modeling based on Rayleigh distribution[C].IEEE Proc Vis Image Signal Proc,2005: 152(1): 129-135.

[3]Narayanan R,Fessler JA,Ma B,et al.Local mismatch location and spatial scale detection in image registration[C].Proc Of SPIE Med Imag,2007,6512:1-8.

[4]Hahn DA,Daum V,Hornegger J.Automatic parameter selection for multimodal image registration[J].IEEE Tran med imag,2010,29(5): 1140-1155.

[5]Katkovnik V,Foi A,Egiazarian K,et al.From local kernel to nonlocal multiple-model image denoising[J].Int J Compu.Vis,2010,86(1): 1-32.

[6]Gomez G,Marroquin JL,Sucar LE.Probabilistic estimation of local scale[C].15th ICPR,2000,3: 790-793.

[7]Sun J,Xu ZB.Scale selection for anisotropic diffusion filter by Markov random field model [J].Pattern Recogn,2010,43(8):2630-2645.

[8]Lindeberg.Feature detection with automatic scale selection[J].Int J Comput Vis,1998,30(2):77-116.

[9]Comaniciu.An algorithm for data-driven bandwidth selection[J].IEEE Trans Pattern Anal Mach Intell,2003,25(2):281-288.

[10]Achanta R,Shaji A,Smith K,et al.SLIC superpixels compared to state-of-the-art superpixel methods[J].IEEE Trans Pattern Anal Mach Intell,2012,34(11): 2274-2281.

[11]Perona P,Malik J.Scale-space and edge detection using anisotropic diffusion[J].IEEE Trans Pattern Anal Mach Intell,1990,12(7):629-639.

[12]Rissanen J.A universal prior for integers and estimation by Minimum Description Length[J].Ann Statistics,1983,11(2): 416-431.

[13]Qin BJ,Gu ZJ,Sun XJ,et al.Registration of images with outliers using joint saliency map[J].IEEE Sign Proc Lett,2010,17(1): 91-94.

[14]Qin B,Shen Z,Local struture matching driven by jonit-saliencystructure adaptive kernel regession[J].[2013-04-15].http://arxiv.org/abs/1302.0494