基于有限段方法的SMA扭转驱动器柔性机构动力分析

邹秀清 董二宝 张世武 许 旻 杨 杰

中国科学技术大学，合肥，230027

0 引言

柔性结构［1］是一种依靠材料的弹性变形来传输运动或力的装置，相比传统的刚性铰链机构，柔性机构在简化结构、减少磨损和提高精度上都有显著的优势。柔性机构通常被应用在精密工程场合以及仿生机械及机器人等领域［1-2］。

在高速、精密以及高性能MEMS应用场合，柔性机构的动力学问题十分突出。因此，柔性机构的动力学特性分析方法的研究是柔性机构学研究的一个重要方向。

文献［3］考虑柔性体变形的动力刚化现象，提出了在有限元方法中引入单元耦合形函数，再根据Kane方程得到包含动力刚度项的一致线性化动力学方程，但是该方法是在结构小变形的前提下推导得出的，对大变形问题并不适用。

文献［4］针对全柔性机器人的动力学分析总结了几种方法:一种是伪刚体法，这种方法虽然可以使柔性体的动力学建模得到很大简化，但是简化造成的误差较大，且复杂柔性机构的伪刚体模型的建立也非常困难;一种是利用有限元软件建立柔性系统的有限元模型，这种方法只限于小变形尺度，可以忽略位形变化对机构动态特性的影响;还有一种就是应用传统的试验方法进行分析，这种方法效率低、耗时长、成本高。

柔性体动力学的有限段方法是基于多刚体动力学理论发展起来的柔性体动力学分析方法，自然计及几何非线性的影响［5］。对于梁式柔性机构，可以方便地应用有限段方法进行离散建模，再利用原有的多刚体动力学理论进行计算分析。

本文采用有限段模型［6］对形状记忆合金(SMA)扭转驱动器的柔性结构部分进行离散建模，结合ADAMS动力学分析软件在系统动力学分析上的优势，对SMA扭转驱动器的柔性结构进行动力学分析。

1 有限段原理介绍

有限段方法的基本思想是:将梁式柔性构件离散为有限的刚性梁段，段间用3个扭转弹簧、3个线性弹簧及与之相应的6个阻尼器相连接，如图1所示。在小应变有限变形的条件下，可用离散的梁段来描述柔性体的惯性特征，用段间的弹簧和阻尼器代表柔性体的弹性和阻尼特性［7］。

图1 梁式柔性机构的有限段模型

在小应变有限变形的情况下，虽然整体的变形比较大，但由于是小应变，每一小段的变形仍然符合小变形条件，所以有限段模型在小变形情况和小应变大变形情况都是适用的。

为了推导梁段之间弹簧的刚度特性，我们首先考察悬臂梁自由端的位移与作用其上的力(矩)的关系。

根据线性梁的理论［8］，在悬臂梁的自由端施加力和力矩，在变形较小的情况下，悬臂梁自由端的位移和转动分量与施加的力和力矩之间的关系如下。

首先，左端固定情况如图2所示，悬臂梁自由端上施加的力F和力矩M与位移u和转动分量θ之间的关系可以表示为

式中，l为梁长度;A为梁截面积;J为梁截面积对X轴的形心二次矩;Iy为梁截面积对Y轴的形心二次矩;Iz为梁截面积对Z轴的形心二次矩;E为材料弹性模量;G为材料剪切模量。

图2 右端点2作用一般载荷的悬臂梁

同理可以得出右端固定情况下的力和力矩与位移和转动分量之间的关系，限于篇幅，这里不再一一列出。

然后，考察柔性梁的弹簧连接有限段模型。为了建立精确的梁模型，弹簧必须精确表示相邻段间的弹性。为推导这个表达式，考察图3所示的两个相邻段Bj和Bk。其中，连接弹簧分别由两个代表相应段弹性的部分组成，同时，连接弹簧代表相应段的伸张、弯曲和扭转特性。

图3 两个典型相邻有限段

每段有12个与其相关的位移和转动分量(与每个端点相关的有6个)。为了定义这些分量，考察如图4所示的任一段Bj。令Gj为Bj的质心。令Oj和Ok为Bj的弹簧与相邻段Bi的弹簧的连接点以及Bk的弹簧与相邻段Bj的弹簧的连接点。令OI、OJ和 OK分别为以 Oj、Gj和 Ok为原点的参考系。令RJ的轴与Bj的主轴连续共线。RI和RK的轴当弹簧未变形时与RJ的轴平行。则OI相对于OJ的位移和RI相对于RJ的转动共有6个自由度。同理，OK相对于OJ的位移和RK相对于RJ的转动共有6个自由度，即与Bj段相关的位移和转动分量有12个。这些位移和转动变量的定义如表1所示。其中，Rk、Rj分别为以OK和OI为原点的参考系。

图4 典型有限段模型

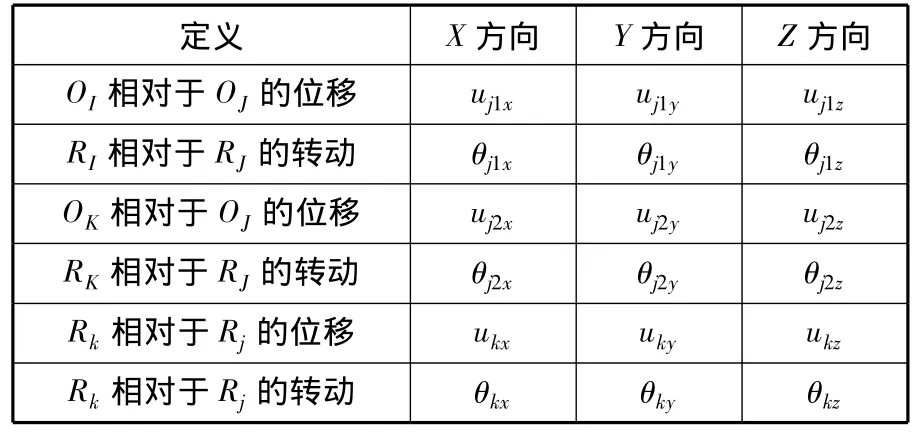
表1 位移和转动变量

Rk相对于Rj的位移和转动变量可表示为

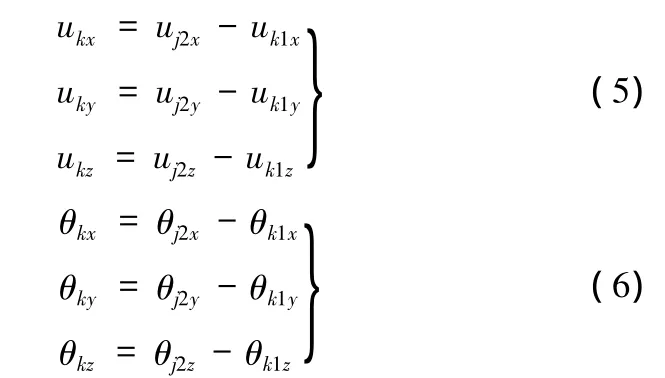
根据式(1)、式(2)，可将 ukx、uky和 ukz表示为

因为在Ok节点处没有质量，也不受外力，所以有:

所以，ukx、uky和 ukz可以表示为

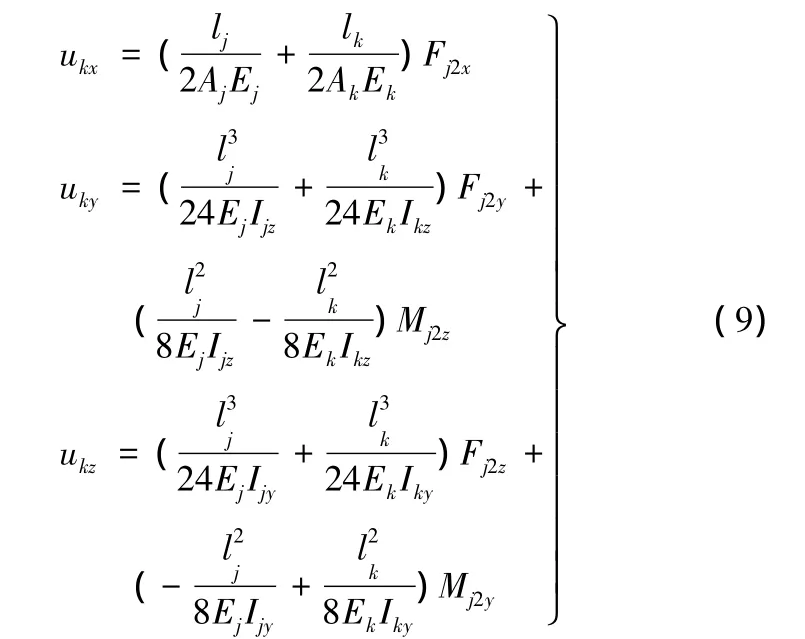
同样，相对转动分量可以表示成

由上可解出 Fj2x、Fj2y、Fj2z、Mj2x、Mj2y和 Mj2z:

其中，系数 a、b、c与相应段的结构、材料参数有关，这里不一一列出，可参考文献［7］。

到此，我们得出了各个段之间的弹簧刚度特性。

2 基于ADAMS宏命令的有限段模型建立与数值计算

为了探讨有限段模型的准确性，我们需要建立梁的有限段模型，为了分析梁的变形情况，需要建立有限段模型的多体系统运动学及动力学方程，如文献［9-10］所描述的，需要计算出每个有限段的广义速率，整理出整个系统的动力学方程组再求解微分方程组而得到系统的特性，模型的建立及求解过程非常复杂而且对于复杂模型更是无能为力。

本文应用ADAMS软件建立有限段多刚体模型进行分析，把动力学方程的建立和求解过程交给软件处理，我们需要做的就是在ADAMS中准确地建立系统的有限段模型。

要在ADAMS中建立有限段模型，关键是创建各个有限段以及在各有限段之间施加的力和力矩。根据有限段模型的特点，有限刚体段和力与力矩的建立是一个重复性的过程，我们利用ADAMS宏命令的循环语句建立模型。先用循环命令建立所有的有限段，然后再用一个循环命令建立各段之间的力和力矩。具体的建立方法如下:如要在第i个有限段part i和第i+1个有限段part i+1之间建立有限段的弹簧力和弹簧力矩，先分别在part i的右端面和part i+1的左端面创建标记点 marker i和 marker i+1，再在标记点marker i和marker i+1之间创建 VFORCE(X、Y、Z三向的直线力)和VTORQUE(X、Y、Z三向的扭转力)。其中，段 part i和段 part i+1之间的力VFORCE的表达式根据式(11)、式(13)、式(15)建立，ukx、uky、ukz分别是 marker i+1 相对于marker i的X、Y、Z轴的移动位移。同样，段part i和段part i+1之间的力VTORQUE的表达式根据式(12)、式(14)、式(16)建立，θkx、θky、θkz分别是marker i+1相对于marker i的X、Y、Z轴的转动位移。

下面，我们探讨有限段模型的准确性。首先，比较直梁的有限段模型和有限元模型在恒力作用下的变形。对厚度h=4mm、宽度b=2mm、长度L=80mm的悬臂直梁，在ADAMS中建立直梁的有限段离散模型，如图5所示，各刚体段间施加的力和力矩按以上有限段模型计算的刚度乘以变形时段间的相对位置变化得到。分析结果如图6所示，从图中可以看出，随着有限段模型不断细化，有限段模型的分析结果不断靠近有限元模型的分析结果。

图5 直梁的有限段模型

图6 直梁静力分析比较

然后，比较曲梁的有限段模型和有限元模型在恒力作用下的变形。在曲梁的有限段模型中，相邻两有限段之间的中性轴并不是平行的，而是有一定曲率夹角存在的，在推导各段之间的弹簧刚性时存在更复杂的耦合情况。但是，随着有限段的不断细化，相邻两段之间的夹角不断减小，对弹簧刚度的影响也不断减小甚至可以忽略。因此，在曲梁应用上，为了简化有限段模型的段间弹簧刚度的推导，在计算段间刚度时，忽略相邻两段之间曲率的影响，将相邻两段近似为直梁段，段间刚度仍然按照直梁的方法推导。任意两小段之间近视为直线段，轴向方向近视为两段相邻点处的切线方向。随着有限段离散的细化，两小段之间的倾角不断减小，这种由近似造成的误差也将不断减小。对厚度 h=4mm、宽度 b=2mm、半径R=50mm的1/4圆弧，在ADAMS中的模型如图7所示，建模方法与直梁一致。分析结果如图8所示，从图中可以看出，随着有限段模型不断细化，有限段模型的分析结果也不断靠近有限元模型的分析结果，且误差与直梁的有限段模型相差不大。

基于以上比较结果可知，尽管有限段模型在曲梁分析上的应用存在忽略梁段之间曲率的简化，但是对有限段离散足够细的模型，其分析结果仍是可靠的。所以，我们认为有限段模型在一定范围内的分析应用是可靠的。

图7 曲梁的有限段模型

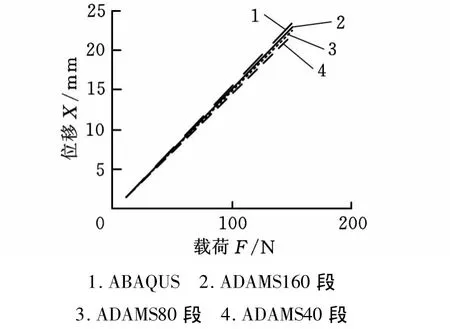
图8 曲梁静力分析比较

3 SMA扭转驱动器的动态特性分析

SMA扭转驱动器的工作原理如图9所示，SMA合金丝按一定规则缠绕在柔性结构及外圆环上，加热SMA合金丝使其收缩带动柔性结构发生变形，从而使中间传动轴孔转过一定的角度。由于本文的主要工作集中在有限段模型建立和SMA扭转驱动器动态特性分析上，SMA扭转驱动器中柔性结构的优化设计以及SMA丝的布置问题在其他文章中有详细介绍，这里不再赘述。

图9 SMA扭转驱动器结构图与实物

本文结合有限段模型和ADAMS动力学分析软件来分析SMA扭转驱动器的动态特性。SMA扭转驱动器的柔性结构在优化设计的过程中是采用B样条曲线来描述曲线形状的，在MATLAB中离散成若干个坐标点。在建立有限段模型时，为了方便，直接以这些离散坐标点为离散位置进行划分。由式(11)～式(16)计算各段之间的弹性特性，在ADAMS中通过应用宏命令建立有限段多刚体模型的方法建立SMA扭转驱动器的离散有限段模型。

首先分析静力情况。在ADAMS中建立SMA扭转驱动器的有限段模型，如图10所示。在缓慢施加的对称恒力10N的载荷作用下，柔性梁厚度为0.4mm的扭转驱动器的输出转角如图11所示。图12显示不同厚度柔性梁的驱动器输出转角。

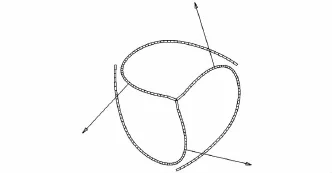
图10 SMA扭转驱动器的有限段模型

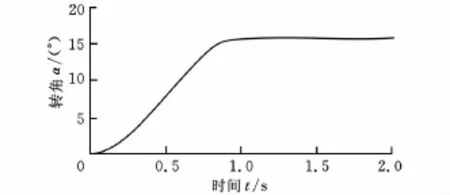
图11 SMA扭转驱动器输出转角曲线

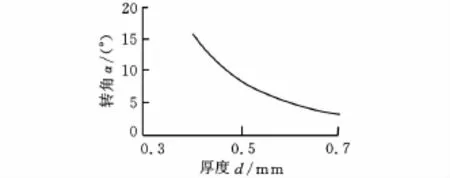
图12 不同厚度下的输出转角

然后，在动载荷情况下观察扭转驱动器的扭转情况。分别施加脉冲载荷和阶跃载荷，观察驱动器的响应情况。

图13显示柔性梁厚度为0.5mm时，在脉冲载荷作用下的时域和频域响应结果。图14显示不同厚度的柔性梁在脉冲载荷下的响应频率，从图14中可以看出厚度越大，响应频率越高。

在阶跃载荷作用下，柔性梁厚度为0.5mm时的扭转响应如图15所示。

4 结论

(1)有限段方法是对梁式柔性机构进行动力学分析的有效方法。

(2)利用ADAMS宏命令在ADAMS中创建有限段模型系统，可以大大简化多刚体系统动力学方程的建立过程。

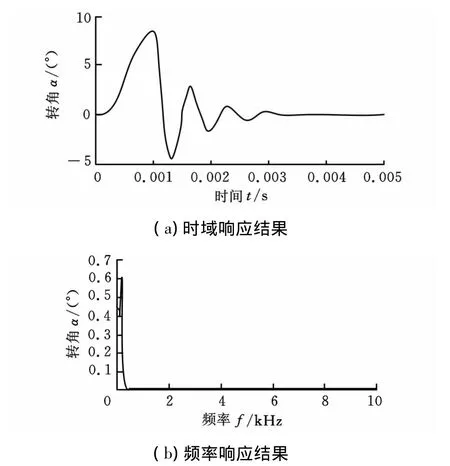
图13 脉冲载荷下扭转响应

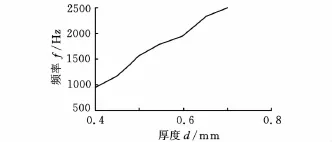
图14 不同厚度下的响应频率

图15 阶跃载荷下扭转响应

(3)将有限段方法应用于SMA柔性扭转驱动器的动力学分析，获得了扭转驱动器的相关动态特性。

［1］Her I，Midha A.A Compliance Number Concept for Compliant Mechanisms and Type Synthesis［J］.ASME Journal of Mechanisms，Transmissions，and Automation in Design，1987，109:348-355.

［2］王振海，张卫红.柔性结构拓扑优化设计发展概况［J］.机械设计，2004，21(3):1-4.Wang Zhenhai，Zhang Weihong.Topological Optimization Design for Flexible Structure［J］.Journal of Machine Design，2004，21(3):1-4.

［3］刘又午，王树新，王建明，等.复杂结构航天器的柔性多体动力学分析［J］.航天器工程，1998，7(3):45-52.Liu Youwu，Wang Shuxin，Wang Jianming，et al.Flexible MultibodyDynamicAnalysisofComplex Structural Spacecraft［J］. Spacecraft Engineering，1998，7(3):45-52.

［4］于靖军，毕树生，宗光华，等.全柔性机器人机构结构动力学分析方法研究［J］.机械工程学报，2004，40(8):54-57.Yu Jingjun，Bi Shusheng，Zong Guanghua，et al.Research on Structural Dynamics of a General Fully Compliant Robotic Mechanism［J］.Journal of Mechanical Engineering，2004，40(8):54-57.

［5］闫绍泽，刘冰清，刘又午，等.柔性多体系统动力学——有限段方法［J］.河北工业大学学报.1997，26(3):1-8.Yan Shaoze，Liu Bingqing，Liu Youwu，et al.Dynamics of Flexible Multibody Systems－The Finite Segment Method［J］.Journal of Hebei University of Technology，1997，26(3):1-8.

［6］Huston R L.Multibody Dynamics Including the Effects of Flexibility and Compliance［J］.Computer and Science，1981，14(5/6):443-451.

［7］李东旭.挠性航天器结构动力学［M］.北京:科学出版社，2010.

［8］刘鸿文.材料力学［M］.北京:高等教育出版社，2004.

［9］金国光，刘又午，张明成，等.含柔性梁机械系统动力学分析的有限段方法［J］.郑州工业大学学报，2000，21(1):23-25.Jin Guoguang，Liu Youwu，Zhang Mingcheng，et al.Finite Segment Method of Dynamic Analysis of Mechanical System with Beam－like Flexible Bodies［J］.Journal of Zhengzhou University of Technology，2000，21(1):23-25.

［10］董龙雷，闫桂荣，余建军，等.带中心刚体的旋转柔性件有限段建模［J］.西安交通大学学报，2001，35(9):977-981.Dong Longlei，Yan Guirong，Yu Jianjun，et al.Finite Segment Modeling of a Rotating Flexible Body with Central Rigid Body［J］.Journal of Xi’an Jiaotong University，2001，35(9):977-981.