旋转机械参数图形多尺度多结构元边缘检测
2013-12-05刘占生苏宪章
张 颖 刘占生 苏宪章
1.东北石油大学,大庆,163318 2.哈尔滨工业大学,哈尔滨,150001
3.中海油安全技术服务有限公司,天津,300456
0 引言
旋转机械在工业领域中的使用十分广泛,振动故障是旋转机械各类故障中出现频次较高,后果较为严重的类型之一。在旋转机械振动信号的各类参数图形中,存在着大量反映设备运行状态的信息,如二维幅频或相频特性曲线、小波图、趋势图、三维谱图、三维阶比图等。通过分析图形信息实现对旋转机械的状态监测是目前该领域的研究热点[1-4]。
在旋转机械故障诊断中,振动信号参数图形的有用信息没有得到很好的利用,这主要是由于施工环境较为复杂,噪声干扰严重,参数图形的边缘特征提取困难所致。数学形态学的主要研究对象是图像的形态特征,此类特征可通过某种结构元素的形态与图像相应形态的对比方式来确定,以此完成对图像的分析、滤波、识别、边缘检测、分割和重建等处理过程[5]。使用数学形态学相关方法分析处理旋转机械振动信号参数图形时,可通过调节结构元素尺度来剔除环境噪声等干扰信息,有效提取参数图形的边缘特征,为进一步的故障诊断扫清障碍。
为此,本文在文献[1]实验的基础上,根据数学形态学Top-Hat变换和Bottom-Hat变换理论,对旋转机械振动信号参数图形进行多尺度滤波增强处理;通过多结构元边缘检测方法对滤波处理后的旋转机械参数图形进行边缘检测。
1 数学形态学的基本原理
数学形态学的基本原理是通过一整套的变换来描述图像的基本特征和结构。数学形态学最基本的2种变换是腐蚀和膨胀,其他变换都是由这2种变换的组合来定义的[6]。
1.1 形态学腐蚀运算、膨胀运算
设A为待处理的灰度图像,B为结构元素,则结构元素B关于图像A的腐蚀与膨胀运算定义为

其中,DA和DB分别是A和B的定义域,位移参数则必须包含在灰度图像A的定义域内。
腐蚀运算可以消除图形中的小成分,可从内部对图形进行滤波;膨胀运算可以填充图形边缘处小的凹陷部分以及图形中比结构元素小的孔洞,可从外部对图形进行滤波[7]。
1.2 形态学开运算、闭运算
形态学开运算、闭运算分别定义为
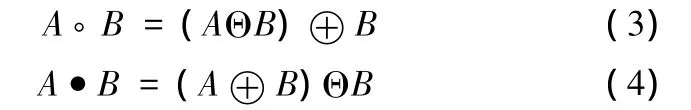
开运算在纤细处分离物体和平滑较大物体边界,具有消除散点、毛刺和小桥等细小物体的作用;闭运算连接两个邻近的区域和平滑边界,具有填充物体内细小孔洞的作用[8]。
1.3 形态学变换
形态学Top-Hat变换是对灰度图像做减去其开运算结果处理,该变换可以提取亮度较高的背景中的较暗区域;形态学Bottom-Hat变换是对灰度图像的闭运算结果做减去原始图像处理,该变换可提取亮度较低的背景中的较亮区域。形态学变换可用来提取目标图像中尺度小于结构元素的峰值和谷值[9]。
Top-Hat变换定义为

Bottom-Hat变换定义为
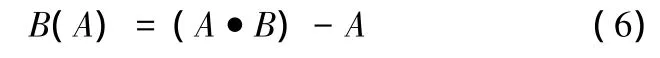
2 多尺度滤波增强处理
形态学腐蚀、膨胀、开、闭4种运算中的1种或2种串联或并联的组合就是形态学滤波运算。多尺度形态学滤波增强处理是通过不同尺寸的结构元素多次对图像进行滤波的,其中多尺度开闭滤波在消除噪声、保持图像细节和提高信噪比等方面优于多尺度腐蚀膨胀滤波,从而在一定程度上优化了灰度图像的有用信息,令后续边缘检测结果更加真实可靠,因此在形态学滤波中应用较多。
多尺度结构元素定义为

其中,B为十字形3×3结构元素,n为滤波尺度,式(7)含义即为大尺度结构元素由小尺度结构元素多次膨胀得到。
为了得到足够平滑的图像,本文采用最大尺度的结构元素Bn对图像进行多尺度开闭滤波增强处理,其表达式为
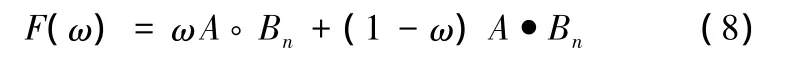
其中,权值ω对最后的滤波增强结果有较大影响,一般取为0.5,本文根据滤波增强处理结果的优劣,取0.3。
图像经过多尺度开闭滤波增强处理后得到足够平滑的低频图像,为获得更全面的有用信息,还需提取图像的高频细节信息。在多尺度滤波增强处理方法中,由于噪声在经小尺度结构元素处理的图像中出现几率较大,并且随着尺度的增加其影响逐渐消失[10],故本文选用带有修正系数的Top-Hat变换(FT(i))和 Bottom-Hat变换(FB(i))来提取图像的高频细节信息。为减小噪声对图像的影响,修正系数设定为公比为0.5的等比数列,此过程完成了不同尺度间小尺度图像特征的平滑处理,具体的表达式如下:

由多尺度开闭滤波增强处理的图像最终由三部分组成:第一部分是图像经最大尺度结构元素开闭滤波增强以后生成的低频平滑图像,该部分包含图像中的大尺度图像信息;第二部分是提取比该滤波增强尺度还小的亮点图像高频特征;第三部分是提取比该滤波增强尺度还小的暗点图像高频特征。至此,一幅灰度图像经多尺度滤波增强处理后生成的图像为[11]

3 多结构元边缘检测算子
在图像边缘检测处理中存在着多种梯度,若在某一像素点处梯度值大,则表示在该像素点处图像的灰度值变化迅速,从而认定该点可能是图像的边缘点。数学形态学边缘检测方法主要是利用形态学梯度来完成图像的边缘检测。若将数学形态学的腐蚀、膨胀、开、闭等基本运算用于图像处理,可构造出合适的形态学梯度算子(经典边缘检测算子)用于图像的边缘检测[12]。
腐蚀型边缘检测算子:

膨胀型边缘检测算子:

膨胀腐蚀型边缘检测算子:

上述3种形态学边缘检测算子是一种非线性的差分算子,这些算子容易实现,在实际中有一定的应用。但是,这些算子对噪声都很敏感,不能在保持较高检测精度的同时又不损失抗噪性能。由于旋转机械振动信号中普遍存在噪声,虽然已经过多尺度滤波增强处理,但仍有少量残留,而且噪声信号和参数图形的边缘又均为频域中的高频分量,因此,为了更好地提取旋转机械振动信号参数图形的边缘特征,应选择抗噪性能优于经典边缘检测算子的方法对参数图形进行边缘检测。根据腐蚀、膨胀、开、闭4种运算抑制噪声的相关特性,本文对式(12)~式(14)做如下改进。
抗噪腐蚀型边缘检测算子:

抗噪膨胀型边缘检测算子:

抗噪膨胀腐蚀型边缘检测算子:

数学形态学边缘检测方法不仅与所使用的边缘检测算子有关,还与结构元素自身特点密切相关,如大小、方向、形状等。在边缘检测过程中,不同结构元素对图像不同边缘细节信息的敏感性各不相同,一种结构元素只能提取图像的一种边缘信息,这不利于保持图像边缘的有用信息。因此,应尽量选用具有不同特征的结构元素对图像进行边缘检测,让每个结构元素都发挥作用,提取出具有其自身特征的边缘信息,这样可以充分保持图像的各种边缘信息,达到既能检测出图像的各种边缘纹理,又能抑制噪声的目的[13]。本文利用抗噪膨胀腐蚀型边缘检测算子(式(17))构造多结构元边缘检测算子,其表达式如下:
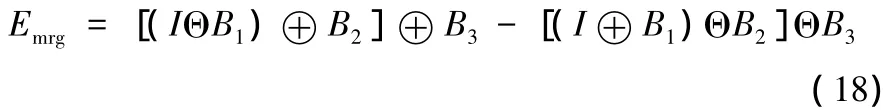
其中,B1、B2、B3为结构元素,尺寸固定不变(3 × 3正方形),B1,B2可取为同一种结构元素,也可取为不同的结构元素。
4 多尺度多结构元边缘检测仿真
为验证多尺度多结构元边缘检测方法的正确性与有效性,本文选取结构元素B1=[1 2 1;2 6 2;1 2 1],B2=[0 1 0;1 1 1;0 1 0],B3=[1 0 1;0 1 0;1 0 1],对含有5% 椒盐噪声的Lenna灰度图像进行多尺度多结构元边缘检测,其中多尺度滤波增强处理使用结构元素B1作为初始结构元素,滤波尺度n取4,多结构元边缘检测算子使用结构元素B1、B2、B3进行检测。图1a为原始灰度图像,图1b为边缘检测结果。从图中可以看出:多尺度多结构元边缘检测方法滤除了Lenna图像中的椒盐噪声,检测出的图像边缘轮廓清晰、纹理明确,信噪比有所提高。该方法边缘检测效果优于经典边缘检测算子边缘检测效果,更适用于含有噪声污染图像的边缘检测。

图1 Lenna噪声污染图像多结构元边缘检测效果
5 旋转机械参数图形边缘检测实例
5.1 实验
旋转机械故障模拟实验在600MW超临界汽轮发电机组轴系试验台上完成,分别进行了转子正常、转子不对中和轴承松动故障的实验。试验台主要包括5个部分,即发电机组轴系、润滑系统、动力系统、供气系统和信号采集分析系统。其中发电机组轴系由9个轴承5跨组成;润滑系统用独立的油路系统对各个轴承供油,每个轴承座均安装BENTLY3000 XL8 mm电涡流传感器,输出为7.87V/mm;动力装置采用55kW变频电机经过FRENIC变频器输出转速和功率,并采用HG0G-C2型变速箱,试验台详细结构布置如图2所示。在实验过程中,采样时间为0.64s,采样频率为转速的32倍,实验时转子最高工作转速为3200r/min,采集的信号经A/D卡传送到计算机,为后续的数据分析做准备[7]。
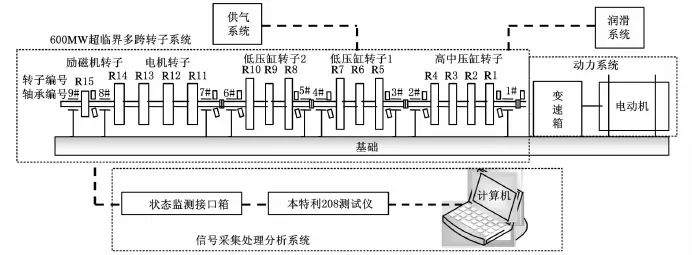
图2 试验台装置组成及其连接图
实验中对转子正常、转子不对中及轴承松动故障,每种采集40个启停机样本,共计120个。首先将每个原始振动信号的采集样本进行处理,生成各自的振动三维谱图,如图3所示。
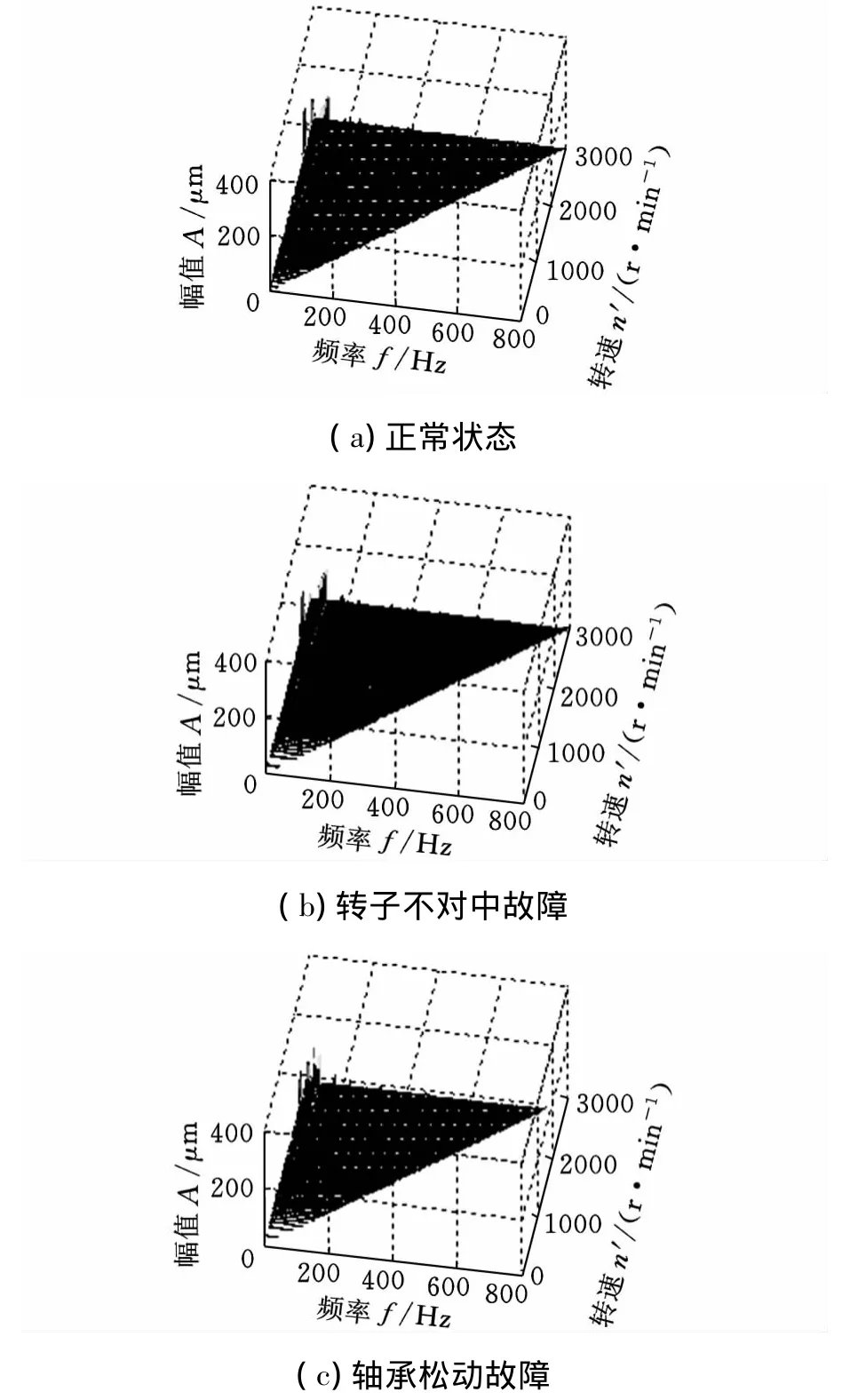
图3 旋转机械各状态三维谱图
5.2 多尺度多结构元边缘检测
根据三维谱图倍频特征明显的特点,将频率作为横轴,转速作为纵轴,像素点灰度值作为该转速下、该频率下幅值的大小,将其转化为二维灰度图形,结果如图4所示。灰度图中明显的竖线为倍频线,与三维谱图中的倍频线相对应。

图4 旋转机械各状态灰度图
为了有效地提取旋转机械振动信号参数图形的边缘特征,本文对图4各种状态下的参数图形进行量化、直方图均衡化等预处理,选取结构元素B4=[1 3 1;3 5 3;1 3 1],B5=[0 1 0;1 1 1;0 1 0],B6=[1 0 1;0 1 0;1 0 1],应用上述多尺度多结构元边缘检测方法对其进行边缘检测。其中多尺度滤波增强处理使用结构元素B4作为初始结构元素,滤波尺度n取4;多结构元边缘检测算子使用结构元素B4、B5、B6进行检测,最终的多尺度多结构元边缘检测结果如图5所示。从图5可以看出:旋转机械振动信号参数图形经多尺度多结构元边缘检测处理后,噪点大幅降低,环境污染噪声基本被滤除干净,有用信息得到保持的同时信噪比大幅提高,边缘鲜明,轮廓清晰,充分保持了图形的细节特征。至此已说明多尺度多结构元边缘检测方法能够有效地提取旋转机械振动信号参数图形的边缘特征,具有较强的抗噪声干扰能力,适合在环境比较复杂、噪声污染较为严重的情况下对旋转机械实施状态监测。

图5 旋转机械各状态边缘检测结果
6 结论
(1)依据数学形态学多尺度图形处理方法,结合Top-Hat变换和Bottom-Hat变换处理方法,选取合适的结构元素,在对旋转机械振动信号参数图形进行有效滤波的同时,可以保持图形的高频细节特征,增强参数图形的有用信息,提高参数图形的信噪比。
(2)运用多结构元边缘检测算子检测旋转机械振动信号参数图形的边缘,能够有效剔除多尺度滤波增强处理过程残留的噪点信息,提取的参数图形边缘特征质量较高。
(3)在实际应用中,结合旋转机械振动信号参数图形及其噪声的特点,多尺度多结构元边缘检测方法可以较好地解决边缘检测精度与抗噪声性能的协调问题,为基于振动三维图形的旋转机械故障诊断奠定基础。
[1]刘占生,窦唯.基于旋转机械振动参数图形融合灰度共生矩阵的故障诊断方法[J].中国电机工程学报,2008,28(2):88-95.Liu Zhansheng,Dou Wei.A Fault Diagnosis Method Based on Combination Gray Co-occurrence Matrix of Vibration Parameter Image for Rotating Machinery[J].Proceedings of the CSEE,2008,28(2):88-95.
[2]Cho S J,Kim J H.Bayesian Network Modeling of Strokes and Their Relationships for On-line Handwriting Recognition[J].Pattern Recognition,2004,37:253-264.
[3]Jack L B,Nandi A K.Fault Detection Using Support Vector Machines and Artificial Neural Networks Augmented by Genetic Algorithms[J].Mechanical Systems and Signal Processing,2002,16(2):373-390.
[4]刘占生,窦唯,王晓伟.基于主元-双谱支持向量机的旋转机械故障诊断方法[J].振动与冲击,2007,26(12):23-27.Liu Zhansheng,Dou Wei,Wang Xiaowei.Fault Diagnosis Approach Based on Principal-component-bispectrum Analysis and Support Vector Machine for Rotating Machinery[J].Journal of Vibration and Shock,2007,26(12):23-27.
[5]Rivest J.Morphological Operators on Complex Signals[J].Signal Processing,2004,84(1):133-139.
[6]杨晖,张继武.数学形态学在图形边缘检测中的应用研究[J].辽宁大学学报:自然科学版,2005,32(1):50-53.Yang Hui,Zhang Jiwu.Research on Application of Mathematical Morphology in Edge Detection of Image[J].Journal of Liaoning University:Natural Sciences Edition,2005,32(1):50-53.
[7]窦唯.旋转机械振动故障诊断的图形识别方法研究[D].哈尔滨:哈尔滨工业大学,2009.
[8]Yu L,Wang R S.Shape Representation Based on Mathem-atical Morphology[J].Pattern Recognition Letters,2005,26(9):1354-1362.
[9]Jackway P T.Improved Morphological Top-hat[J].Electronics Letters,2000,36(14):1194-1195.
[10]郝如江,卢文秀,褚福磊.滚动轴承故障信号的多尺度形态学分析[J].机械工程学报,2008,44(11):160-165.Hao Rujiang,Lu Wenxiu,Chu Fulei.Multiscale Morpholo-gical Analysis on Fault Signals of Rolling Element Bearing[J].Journal of Mechanical Engineering,2008,44(11):160-165.
[11]Mukhopadhyay S,Chanda B.Fusion of 2d Grayscale Images Using Multi-scale Morphology[J].Pattern Recognition,2001,34(12):1939-1949.
[12]Maragos P.Tutorial on Advances in Morphological Image Processing and Analysis[J].Optical Engineering,1987,26(7):623-632.
[13]Song J,Delp E J.The Analysis of Morphological Filters with Multiple Structuring Elements[J].Computer Vision Graphics and Image Processing,1990,50(3):308-328.
