油压减振器的特性分析

樊友权 柯 坚 李俊琦 刘桓龙 于兰英

1.西南交通大学，成都，610031 2.株洲联诚集团减振器有限责任公司，株洲，412001

0 引言

目前，我国传统减振器的性能测试是通过进口国外试验台进行的，这不仅需要耗费大量的人力物力，而且试验台大多对减振器外形尺寸有严格要求［1］。也有学者利用非线性数学模型对减振器进行特性研究，但多属理论经验公式，并不能准确反映减振器的实际工作情况。本文以一系垂向油压减振器为研究对象，利用有限元仿真软件对其内流场进行可视化的仿真分析，为减振器的性能预测、结构优化提供现实指导意义。

1 减振器理论研究

1.1 工作原理

油压减振器的基本结构如图1所示，其中活塞阀和底阀是单向挡板阀，阻尼调节阀由3种调节阀组成，其位置分布与结构如图2所示，其中1为调压阀，2为补充阻尼阀，3为主阻尼阀，三者的开启压力关系为:pk3＜pk2＜pk1［2］。

油压减振器的基本动作是拉伸与压缩，无论处于何种工况，油液均从有压腔经阻尼调节阀产生阻尼作用，耗散能量，吸收车体振动。

图1 减振器物理模型

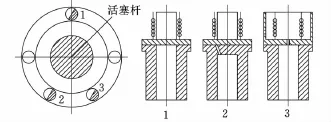
图2 减振器调节阀位置

当活塞杆受力拉伸时，活塞下腔体积增加，底阀开启，油液由储油箱流入活塞下腔。而上腔体积减小，活塞杆单向阀处于关闭状态，上腔中的油液压力增大，产生压力作用在活塞有效面积上，产生拉伸阻尼力。上腔油液经阻尼调节阀流入储油缸中。

当活塞杆受压缩力时，活塞下腔体积减小，压力增大，底座单向阀处于关闭状态。上腔体积增加，压力减小，活塞单向阀导通，下腔有压腔的油液经活塞单向阀流入上腔，由于此部分油液体积大于上腔增加体积，故油液经阻尼调节阀流入储油缸。压力作用在活塞杆面积上，产生压缩阻尼力。

1.2 减振器理论流量分析

当减振器在外力作用下产生振动时，减振器的阻尼调节阀会根据不同的振动速度由不同的阻尼阀参与工作。根据典型结构减振器实测数据可知，减振器在振动速度v≤0.04m/s时，只有调节阀3工作;0.04m/s＜v≤0.13m/s时，调节阀2和调节阀3工作，而调节阀1不工作;振动速度v＞0.13m/s时，三组调节阀同时工作［2］。故在对减振器进行理论分析的过程中，需要分工况进行讨论。

根据流量连续性方程，油液流经孔口时，当出流流体与孔口边壁呈线性接触且l/d≤2(l为孔的通流长度，d为孔径)时，孔口出流公式为

式中，Qe为孔口流量;Cd为流量系数;A为孔口截面积;Δp为孔口两端压力差;ρ为油液密度。

对于阻尼调节阀孔长径比最大值，调压阀取1.75，故经过阻尼调节阀孔n的流量为

式中，Qen为阻尼调节阀孔流量;Cd=0.82;An为阻尼阀孔横截面积;p2为活塞上腔压力;pkn为阻尼阀开启压力(主阻尼阀取储油缸的压力p0)。

根据挤压油膜理论［3］，当补充阻尼阀或调压阀阀芯开启高度为h时，其流量为

式中，Kqn为阻尼调节阀孔流量参数;h为阻尼调节阀阀芯开启高度;p'kn为阀芯开启高度为h时的阀出口压力。

根据牛顿第三定律可知，当补充阻尼阀或调压阀阀芯开启高度为h时，有

式中，Kxn为阻尼阀调压弹簧刚度;xn0为调压弹簧预压缩量。

减振器总流量Q等于每个工况下参与工作的各个阻尼调节阀的阀孔流量之和，这里不作详述。

从体积守恒方面考虑，在拉伸工况中，减振器总流量应等于活塞上腔体积减少量，即

在压缩工况下，减振器总流量应等于活塞下腔体积减少量与活塞上腔体积增加量之差，即

式中，A1为下腔截面积;A2为上腔截面积;v为活塞振动速度。

1.3 减振器理论阻尼力分析

当活塞杆顶端受到振幅为Smax、频率为ω的激励时，活塞相对于油缸也做相同的运动。当激励信号 S(t)=－ Smaxcosω t时，有

在拉伸工况下，活塞单向阀关闭，底阀单向阀开启，故活塞下腔压力p1等于储油缸压力p3。根据流量分析，可以得出经过阻尼孔的流量Qe。

若作用在活塞上的拉力为Fe，则

根据体积变化关系，有

将p2代入式(9)中，得

其中，A3=A1－A2，实际上就是活塞杆的截面积。在拉伸过程中，p1A3相对于拉伸阻力可以忽略不计。所以拉伸阻力可近似表示为

在压缩工况下，活塞单向阀开启，底阀上的单向阀关闭，此时p2=p1，经过阻尼孔的流量Qc为

压缩阻尼力为

1.4 阻尼调节阀阀芯位移分析

在利用ANSYS CFX进行流体仿真计算过程中，经分析可知，对阻尼调节阀的阀芯开启高度与活塞上腔压力、阻尼调节阀弹簧高度及压缩量有关，现对其位移进行理论计算。

根据牛顿第二定律可知:物体随时间变化之动量变化率与所受外力之和成正比。在补充阻尼阀参与减振器工作的情况下，可以以不同的形式将阀芯部分的流体受力表示为

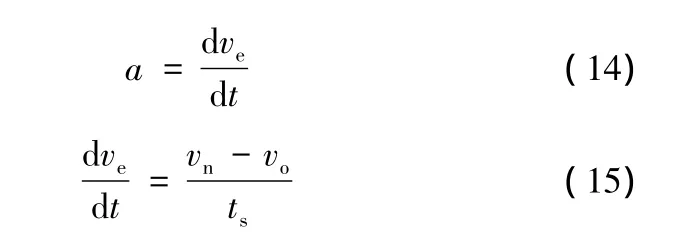
式中，m为阻尼阀阀芯处的流体质量;a为流体加速度;F为阻尼阀受到的活塞上腔压力;Fsp为阻尼阀弹簧压力;ve为阻尼阀的速度;ts为时间步长;vo为初始速度;vn为经过时间ts后的流体速度。

而vn根据位移s可以表示为

其中，Ksp为阻尼阀阀芯弹簧刚度，通过对上述方程求解，可以得出阀芯位移dn为

2 减振器仿真计算

本文主要针对油压减振器典型工况进行CFD仿真计算，即活塞振动速度范围为0.05～0.3m/s。首先需要根据减振器结构与内流场分布情况，利用Pro/E对其内流场进行三维几何建模。然后导入有限元网格划分工具中，根据网格变形程度选择不同的网格类型对模型进行网格划分。最后根据实际流场特征，基于ANSYS CFX平台，对减振器内流场进行仿真计算，得出内流场分布特征与阻尼特性曲线。

2.1 仿真建模

通过对一系垂向油压减振器的工作原理与工作过程的分析可知，减振器在工作过程中有拉伸与压缩两种工况，而液压油在这两种工况中的流动方向不同，故两种工况下的流体模型不同，需要分别建立。另外，减振器的3个阻尼调节阀开启压力也不相同，当其在外力作用下振动加剧时，阻尼调节阀随着上腔压力的增加依次打开，不同的阻尼调节阀组合在一起工作，实现减振器各种不同的阻力特性。

图3为3个阻尼调节阀的模型。对于这部分的模型，虽然补充阻尼阀与调压阀阀芯处需利用CFX动网格技术，但鉴于结构的复杂性和位移量较小等因素对此部分模型均划分为四面体网格，见图 3d、图 3e、图 3f。

对于油缸部分的油液，由于其位移量较大，为不影响计算精度故划分为六面体网格。整体三维模型如图4所示，其中图4a、图4b为拉伸和压缩两种工况下的三维模型，图4c、图4d为其有限元模型。

图3 阻尼调节阀模型

图4 流场整体模型

2.2 仿真条件

针对本文所述的典型工况(0.05～0.3m/s范围内)，选取4个不同的振动速度对减振器内流场进行仿真计算。根据实际情况以及流量特性，边界条件设置如下:油液流动状态为紊流，采用标准κ－ε模型［4］;进出口边界均设置为压力边界，数值为储油缸的压力值;流体与缸体的接触面为滑移边界。

活塞杆根据拉伸与压缩工况，分别加载正弦和余弦函数;阻尼阀阀芯位移根据式(10)利用ANSYS CFX CEL语言编写位移函数。具体参数见表1。

表1 基本参数表

2.3 阻尼阀内流场分析

通过对减振器的工作原理与工作过程的分析可知，阻尼调节阀无论是在拉伸工况还是在压缩工况都起主要的阻尼调节作用，因而对其内流场进行分析，可以更好地把握减振器内部结构参数对减振器性能的影响。

根据文献［2］，通过对一系垂向油压减振器的典型结构进行实验，可以得到如下结论:当活塞振动速度0.04≤v≤0.13m/s时，只有主阻尼阀和补充阻尼阀参与工作;当v＞0.13m/s时，3个阻尼阀共同参与减振器工作。因此当活塞振动速度为0.05m/s、0.1m/s时，对主阻尼阀和补充阻尼阀进行流场分析;当活塞振动速度为0.2m/s、0.3m/s时，对调压阀进行流场分析。

图5、图6分别为活塞振动速度为0.05m/s和0.1m/s时主阻尼阀压力云图与速度矢量图;图7、图8为速度在0.05m/s和0.1m/s时补充阻尼阀的压力云图与速度矢量图;将图6和图8中的主阻尼阀和补充阻尼阀孔处的压力云图放大，并截取在该振动速度范围内振动速度较低时的压力云图，如图9和图10所示。图11、图12为速度在0.2m/s和0.3m/s时调压阀的压力云图与速度矢量图。

通过对以上各调节单元在不同振动速度情况下的流场特征进行分析，可以得出以下结论:

图5 速度为0.05m/s时主阻尼阀压力云图和速度矢量图

图6 速度为0.1m/s时主阻尼阀压力云图和速度矢量图

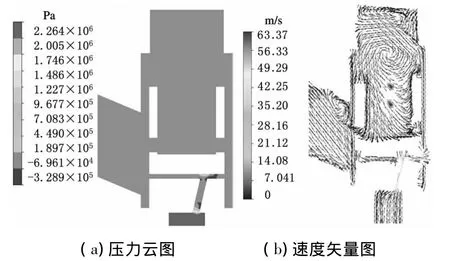
图7 速度为0.05m/s时补充阻尼阀压力云图和速度矢量图

图8 速度为0.1m/s时补充阻尼阀压力云图和速度矢量图

(1)减振器在4种不同振动速度情况下，阻尼阀流场趋势大致相似，油液均是在过流断面突然减小的地方速度达到最大而压力最小，通过阻尼调节单元时产生阻尼作用来耗散振动能量。

(2)对于主阻尼阀，由于油液在经过阻尼阀孔时，过流断面突然减小，故此处油液速度突然增大，而压力迅速减小，沿阀孔轴向方向呈阶梯状向阻尼阀内部递减，在阀孔入口的两侧分别出现一定范围的负压区。通过观察图9可知:负压区的范围与强度会随着速度的增加而增大;油液经阻尼阀孔后速度达到最大值并直接冲击到阻尼阀顶部，由于受到阀腔顶部的阻挡改变流动方向形成涡流，涡流区的范围随着振动速度的增加而增大;一部分油液在流出阻尼阀孔后直接流向阀出口腔，其速度高于受阀腔顶部阻挡后流向出口腔油液的速度，故在出口腔也会形成一定范围的涡流。

图9 速度为0.1m/s时主阻尼阀孔压力云图放大

图10 速度为0.1m/s时补充阻尼阀孔压力云图放大

图11 速度为0.2m/s时调压阀压力云图和速度矢量图

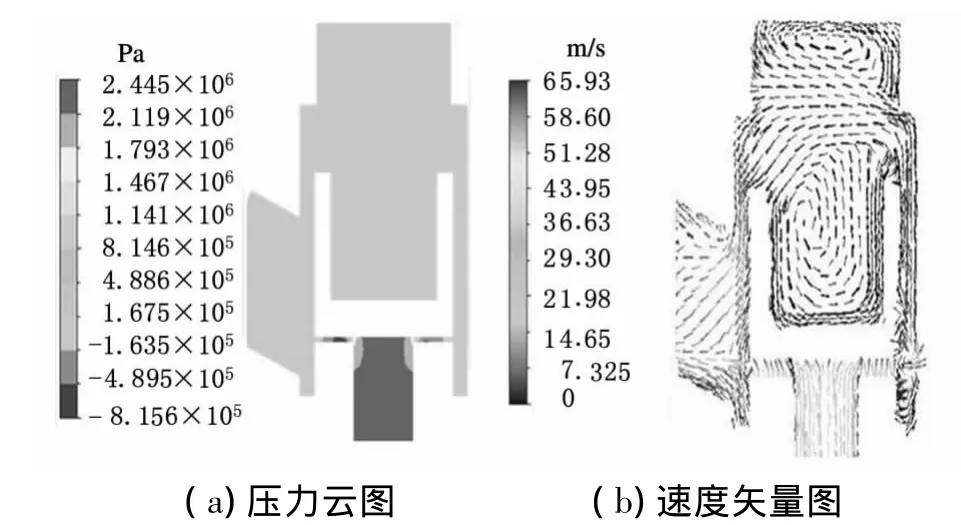
图12 速度为0.3m/s时调压阀压力云图和速度矢量图

(3)对于补充阻尼阀，油液经补充阻尼阀孔后速度达到最大值，由于补充阻尼阀孔向右倾斜，并且受到阀芯底部壁面的阻挡，油液流向阀腔四周壁面，右侧油液由于距离四周壁面近其速度远大于左侧油液速度，故在受到壁面挤压冲向阀腔顶部时受到顶部壁面阻挡改变流动方向形成涡流;此部分油液与主体油液汇合形成第二部分的涡流;阻尼阀孔喷射出的油液在阀芯底部集聚，造成阀芯底部小范围出现高压区，而且通过对比可知高压区的范围随着减振器振动速度的增大而增大。

(4)对于调压阀，由于阀腔入口变小，故油液压力会小范围减小，在入口处两侧出现小范围的低压区;由于油液经阀芯出口，过流断面突然减小，故油液速度突然增大，而压力减小，出现了大范围的负压区;调压阀阀芯出口流道转折处的流速达到最大，主要是由于此处的过流断面突然减小引起的。在阀腔内部，由于油液经过流断面很小的阀腔壁，故油液以较高速度冲击阀腔顶部，受到阀腔顶部的阻挡而形成涡流。另一方面，涡流会阻挡阀腔壁面的主流体，导致油液改变运动方向，向下运动后受到阀芯阻挡而形成另一较大范围的漩涡。

2.4 阻尼阀特性分析

根据上述仿真条件与内流场分析，在ANSYS CFX的后处理中对活塞杆上下表面提取阻尼力，从而得到可以表示减振器阻尼特性的F－s和F－v曲线。将仿真得到的F－s曲线、F－v曲线分别与实验数据对比，如图13所示。

由图13中曲线参数可以得出减振器在整个工况下的参数，如表2所示。

通过将CFD仿真得出的数据与实验数据对比可知，最大阻尼力偏差最大为4.50%，最小阻尼力偏差最大为5.28%，阻尼力系数偏差为4.38%，而以上数据均小于经验公式得出的数据，故采用CFD仿真方法对减振器进行仿真计算要明显优于经验公式，能更准确地反映真实流场。根据铁道部油压减振器通用技术标准［5］规定减振器性能判别标准:减振器示功图不对称率在±10%范围内;减振器阻尼力误差在±15%范围内。仿真结果各项技术符合要求。

3 结论

(1)对于结构复杂模型，可以通过分析其运动位移量来划分不同的网格类型后，在ANSYS ICEM平台下将其组装，这样不仅可以保证网格质量与计算精度，还缩短了仿真时间。

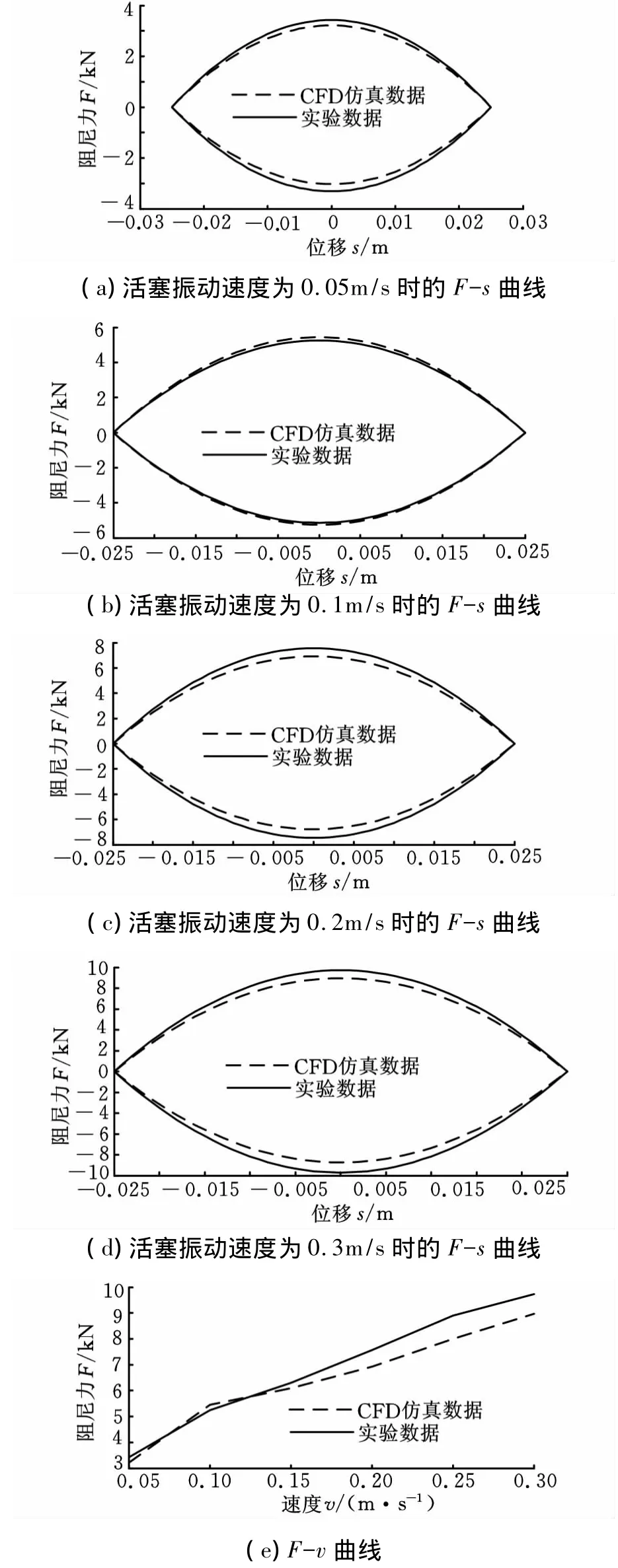
图13 仿真与实验数据对比图

(2)基于ANSYS CFX流体仿真平台，可以可视化地观察减振器内流场的分布特征，并最终得出阻尼特性曲线，预测减振器的性能。

(3)CFD仿真数据与实验数据的对比结果表明，阻尼参数和不对称率的偏差均在规定范围内，故建立的模型与仿真系统真实可信，与传统理论经验公式更能接近真实流场并且对内流场分布特征可更好地把握，为减振器的性能预测提供了一种有效的方法。

表2 性能参数表

［1］樊友权.高速列车减振器试验台的研制［D］.成都:西南交通大学，2004.

［2］丁问司，巫辉燕.铁道车辆油压减振器三维流场动态仿真［J］.机械工程学报，2011，47(6):130-137.Ding Wensi，Wu Huiyan.Dynamic Simulation of 3D Flow Field of Train Damper［J］.Journal of Mechanical Engineering，2011，47(6):130-137.

［3］王福军.计算流体动力学分析－CFD软件原理和应用［M］.北京:清华大学出版社，2004.

［4］王文林.高速列车可调式线性油压减振器的设计理论与应用研究［D］.杭州:浙江大学，2001.

［5］中华人民共和国铁道部.TB1491－83机车车辆油压减振器通用技术条件［S］.北京:中国标准出版社，1984.