四格表资料非条件精确检验的SAS实现

军事医学科学院生物医学统计学咨询中心(100850) 柳伟伟 胡良平 周诗国

对于四格表资料的分析，在大样本时通常选用χ2检验，小样本时一般选择Fisher精确概率法。Fisher精确概率法属于条件精确检验，它通过将四格表的行、列合计固定，从而去掉冗余参数，也就是未知的总体率π。与之相对的是非条件精确检验，该方法由Barnard提出〔1〕，它被认为比Fisher精确检验具有更高的检验效能〔2〕。在SAS软件中，通过FREQ过程能够很容易的实现χ2检验与Fisher精确检验，但是现有的SAS过程无法实现非条件精确检验。本文根据非条件精确检验的原理，编制出了非条件精确检验的SAS实现程序。

原理与方法

四格表的一般形式可见表1:

表1 四格表的一般形式

设A1和A2分别对应于两个来自不同总体的独立样本，样本量分别为n1和n2;B1和B2分别表示阳性结果与阴性结果;n代表总例数。想考察两个总体率π1与π2之间的差异是否有统计学意义，原假设为H0:π1=π2=π。根据二项分布原理，在原假设成立的条件下，表1出现的概率为:

Fisher精确检验通过固定行、列合计，可以将上式中未知的π去掉，同时将表1出现的概率表达为超几何概率的形式。然后在行、列合计固定的约束条件下，计算频数变动时的各个四格表出现的超几何概率，求出等于观察值或比观察值更极端的四格表出现的概率之和，就得到了检验的P值。该检验中需要计算概率的四格表的数目 k=min(n1，n2，m1，m2)+1。

在非条件精确检验中，仅仅假定两个独立样本的例数n1与n2固定，阳性与阴性结果出现的频数m1和m2是不固定的。对于一个给定的总体率π，在行合计固定而列合计变动的条件下，根据式(1)计算频数变动时各个四格表出现的概率，求出等于观察值或比观察值更极端的四格表出现的概率之和，记作P(π)。此时需要计算概率的四格表的数目k=(n1+1)×(n2+1)。对于双侧检验，P(π)可以表示为:

式中T代表衡量四格表极端程度的统计量，T0代表观察到的四格表所对应的统计量值。与Fisher精确检验类似，在非条件精确检验中，T的定义可以有多种方式〔4〕。其中计分统计量可表示如下〔5〕:

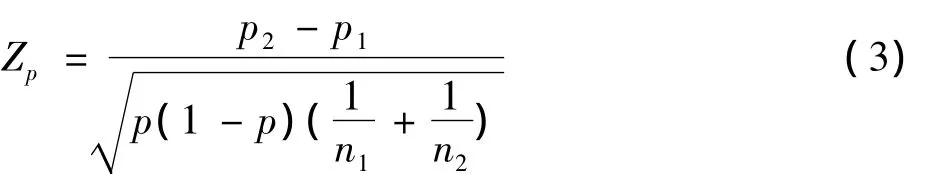
式中 p1=a/n1，p2=c/n2，p=(a+c)/n。如果 a=c=0 或 b=d=0，则 Zp=0。

由上可知，对于每一个特定的π，都可算得一个P(π)。现在的核心问题是:如何去掉未知总体率π。在非条件精确检验中，首先让π在其可能的取值范围〔0，1〕内变动，针对每个π 计算P(π);然后取 P(π)的上确界作为检验的最终P值。这样就达到了去除冗余参数π的目的，它能够保证实际犯Ⅰ类错误的概率始终不会超过检验水准〔6〕。非条件精确检验的P值可表示如下:

在上式中，总体率π是在〔0，1〕内变动的，然而，这个范围内的有些取值并不被观察到的数据所支持，也就是说由观察数据来判断的话，总体率取这些值的可能性很小。基于此，Berger和Boos提出让π在其1－γ可信区间内变动，γ取较小的值，例如0.001或0.0001，该可信区间是通过观察到的四格表数据计算

式中Cγ表示π的1－γ可信区间。

SAS程序实现

根据上文中所介绍的原理，本文针对双侧检验编制了非条件精确检验的SAS实现程序，对于单侧检验，只要稍加改动就可以。由于Z2p=χ2，为了使程序更为简洁，在编写该程序的时候使用χ2统计量代替Zp统计量，通过χ2值衡量四格表极端程度。另外，我们所编制的程序计算出的P值是与式(5)相对应的，如果读者想让总体率π在〔0，1〕内变动，根据式(4)来计算检验的P值，只需将程序中进行区间估计的内容去掉就可以了。

实现四格表非条件精确检验的程序可以分为5个部分:第一部分用于估计总体率π的1－γ可信区间;第二部分用于计算观察到的四格表所对应的χ2值;第三部分用于确定等于观察值或比观察值更极端的四格表;第四部分用于计算给定总体率π时各个四格表的概率，求出等于观察值或比观察值更极端的四格表出现的概率之和;第五部分用于确定P(π)的上确界，计算最终的P值。

具体程序如下:的〔7〕。此时非条件精确检验的P值为:

程序中的宏参数＆a、＆c分别代表两组的阳性例数，也就是表1中的a和c;＆n1、＆n2分别代表两组的样本例数，＆n代表总例数，＆gamma代表显著性水平;＆ite代表总体率的变动范围被划分成的小区间的个数，也就是π的取值个数减1。

实例应用

研究乙肝免疫球蛋白预防胎儿宫内感染HBV的效果，将33例HbsAg阳性孕妇随机分为预防注射组和非预防组，结果见表2。问两组新生儿的HBV总体感染率有无差别?

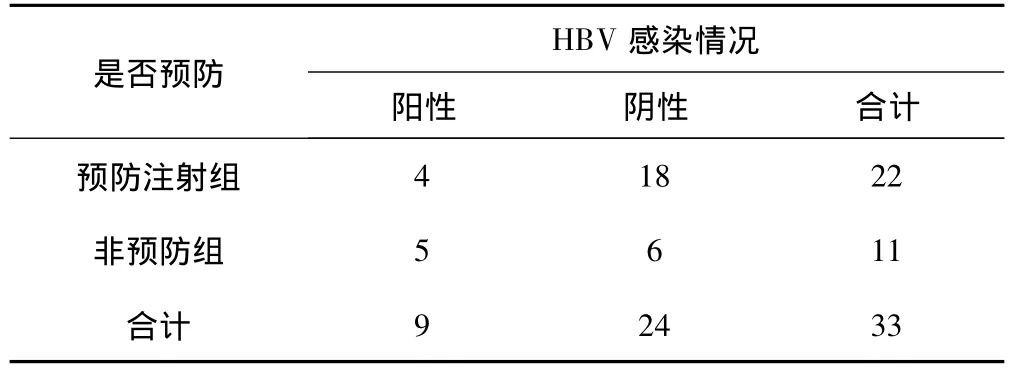
表2 两组新生儿HBV感染率的比较

运行非条件精确检验的SAS程序，程序写法为:

该例中非条件精确检验的的P值为0.11778，此时对应的总体率π的取值为0.26727。对于本例，也可以算得Fisher精确检验的P值为0.1210，该值略大于非条件精确检验的结果。

讨 论

为了验证本文中SAS程序的正确性，把该程序应用于多个实例，将产生的结果与Statxact软件的分析结果进行了反复比较，证明了本程序的运行结果是可靠的〔8〕。此外，我们也对文献〔6〕中的例子进行了计算，结果与该文也是相同的。从运算速度来看，该程序也是比较令人满意的:对于小样本和中等规模样本的资料，能够很快得出运行结果;对于大样本资料，耗时也不会很久。综合来看，一般资料的非条件精确检验，都可以在数分钟之内运算完成。

笔者的程序不但可以作为SAS软件四格表资料统计分析的补充，经过适当改进，还可以用于不同方法之间的比较研究，以及实现其他一些定性资料的精确检验。

1．Barnard GA．Significance test for 2 ×2 tables．Biometrika，1947，34:123-138．

2．Lydersen S，Fagerland MW，Laake P．Recommended tests for association in 2 ×2 tables．Statistics in Medicine，2009，28(7):1159-1175．

3．SAS Institute Inc．SAS/STAT 9．2 User's Guide．Cary，NC:SAS Institute Inc，2008:1675-1829．

4．Sahai H，Khurshid A．On analysis of epidemiological data involving a 2×2 contingency table:an overview of Fisher's exact test and Yates.correction for continuity．Journal of Biopharmaceutical Statistics，1995，5(1):43-70．

5．Suissa S，Shuster JJ．Exact unconditional sample sizes for the 2 ×2 binomial trial．Journal of the Royal Statistical Society，1985，148(4):317-327．

6．韩宏，王彤，何大卫．完全随机设计两样本率比较的非条件确切检验方法．中国卫生统计，2005，22(4):207-209．

7．Berger RL，Boos DD．P values maximized over a confidence set for the nuisance parameter．Journal of the American Statistical Association，1994，89(427):1012-1016．

8．Statxact．Statxact 9 user's manual．Cytel Co．，2010:471-573．