样本量及删失率对生存分析模型有效性和偏倚性的影响*

中山大学公共卫生学院医学统计与流行病学系(510080) 陈 雯 陈 昂 夏英华 凌 莉

由于生存分析在处理删失数据上具有无法替代的作用，因此在医学研究中应用非常广泛。Cox比例风险回归模型(Cox proportional hazards regression model，Cox模型)由于不要求估计资料的分布类型，在医学研究的应用较为广泛〔1〕。加速失效时间模型(accelerated failure-time model，AFT模型)由于具有能够直接分析协变量与对数生存时间之间的回归关系，结果较Cox模型更为简单、直观，易于理解等特点〔2〕，在实际研究中也得到越来越多的应用。

实际研究中，很多因素都会影响研究的样本量和删失率。不同的样本量和删失率会对生存分析模型带来怎样的影响，是多数研究者都非常关心的问题。Cox模型要求样本含量要足够大，一般地，完全数据例数应为模型中变量数的10倍以上〔1〕。此外，Cox模型采用偏似然函数进行参数估计，在删失数据较多时估计结果不够理想〔3〕。但目前国内尚未见针对样本量和删失率对AFT模型的有效性和偏倚性的影响，及对两类模型影响大小比较的研究。本研究拟通过统计模拟，探讨不同样本量和删失率对两种模型参数估计偏倚性和有效性的影响，为根据实际资料特点选用适合的生存分析方法提供参考依据。

资料与方法

社区美沙酮维持治疗(methadone maintenance treatment，MMT)是针对阿片类物质成瘾者的替代疗法，其要求受治者每天口服一定剂量的美沙酮，并长期维持治疗，维持时间越长，治疗效果越好〔4〕。本研究选取广东省首批开设的两个社区美沙酮维持治疗试点门诊自开诊(2006年1月)至2009年11月期间收治的所有满足《海洛因成瘾者社区药物维持治疗试点工作暂行方案》〔5〕中纳入、排除标准，且签署知情同意书的受治者，共612人作为研究对象。通过首次参加治疗时的问卷调查和日常病例记录获取受治者的社会人口学特征、吸毒史、每日是否参加治疗、每日服药剂量等信息。

1．生存分析方法应用于MMT数据时，相关概念的定义

生存时间:受治者参加MMT的维持时间;

结局事件:受治者退出治疗，按照国家相关规定，退出治疗是指受治者连续7天以上(含7天)未到门诊服药;

删失:①受治者到研究结束仍然在治;②受治者在研究过程中转诊至其他门诊接受治疗，无法进行随访。

2．Cox比例风险回归模型的应用

假设在t时刻尚未退出治疗的受治者在后一瞬间的退出风险 h(t，Z)=h0(t)exp(β'Z)=h0(t)exp(β1Z1+β2Z2+…+βmZm)，其中h0(t)是基准风险率函数，代表全部协变量均为0时的个体危险率，h0(t)是随时间变化而变化的未知函数;h(t)随协变量变化的形式假定为指数函数exp(β'Z)，β为协变量Z的系数。

3．AFT 模型的应用

AFT 模型表达式为:Yi=μ+α'Zi+σεi，其中 Yi为维持时间的自然对数，Zi为协变量，α'=(α1，…，αn)为回归系数向量，σ为尺度参数，ε为服从特定分布的随机误差项。该模型要求生存时间服从某一特定的分布类型，常见的分布类型有Weibull分布、指数分布、对数logistic分布。

(1)指数分布

分布函数 S(t)=e－λt

风险函数h(t)=λ

(2)Weibull分布

分布函数 S(t)=e－λtγ

风险函数 h(t)= λγtγ－1

(3)对数logistic分布

上式中，γ为形状参数，γ＞1时危险率随时间递增，γ≤1时危险率随时间递减;λ为尺度参数。在本研究中，λ大则表示退出风险高，维持时间短，反之则表示退出风险低，维持时间长。

对生存分布数学模型的拟合有多种方法，粗略的分为图示法和数值法〔6〕。本研究采用数值法考察不同分布的参数模型对维持时间的拟合效果，根据最小信息量原则，选择最优的分布模型。

4．数据模拟

本研究将调查获得的全部MMT受治者看作总体，以Cox模型和AFT模型对平均服药剂量这一协变量的参数估计和假设检验为金标准(服药剂量是MMT维持时间最重要的影响因素〔7〕，故本研究以剂量为例，将受治者按平均服药剂量分为高剂量(＞60mg/d)、中剂量(30～60mg/d)、低剂量(＜30mg/d)三组，以高剂量组为参照)，通过抽样模拟和删失模拟考察两种方法参数估计的有效性和偏倚性。

抽样模拟的实现:从全部612例研究对象中，重复抽取样本量为50、100、200、300、400、500 的样本各500次。

删失模拟的实现:根据设定的删失比例(20%、30%、40%、50%、60%、70%、80%、90%)，计算出需增加的删失人数，再随机地从全部已发生结局的研究对象中抽取相应的人数。删失时间由完全时间与服从0～1之间均匀分布的随机数相乘获得。不同的删失比例分别模拟500次。

有效性的评价指标:模拟样本参数的假设检验与总体参数假设检验一致的例数n占模拟样本总数N的比例。

偏倚性的评价指标:为了使两种方法有可比性，选用模拟样本的回归系数与总体回归系数的相对误差的均值作为评价偏倚性的指标。式中N为模拟样本的例数，βn为第n个模拟样本的回归系数，β0为总体回归系数。

5．计算分析实现

应用SAS9.1软件包进行分析。Cox模型、AFT模型分别用PROC PHREG、PROC LIFEREG过程实现。抽样模拟和删失模拟采用自行设计的SAS程序实现。

应用实例

1．AFT模型的拟合

采用数值法考察维持时间的分布。由表1可见，取对数logistic分布时的对数似然比最大。根据最小信息量原则，取对数logistic参数模型时AIC值最小，所以把它作为最后的拟合结果。

表1 MMT维持时间数据的AFT模型拟合结果

2．生存分析模型参数估计的有效性和偏倚性

(1)有效性

由表2～3，图1～2可知，在各种样本量和删失率情况下，Cox模型的有效性均比对数logistic模型低。随着样本量的减少和删失率的增高，两模型的有效性均降低，且Cox模型降低的速度更快。删失率超过60%时，有效性加速下降。

对于大样本(≥500)或删失率较小(≤30%)的数据，两类模型的有效性均较高，且基本相等。样本量不足200或删失率大于70%时，两类模型的有效性均较差。

表2 不同样本量下Cox模型和对数logistic模型的有效性(power)比较

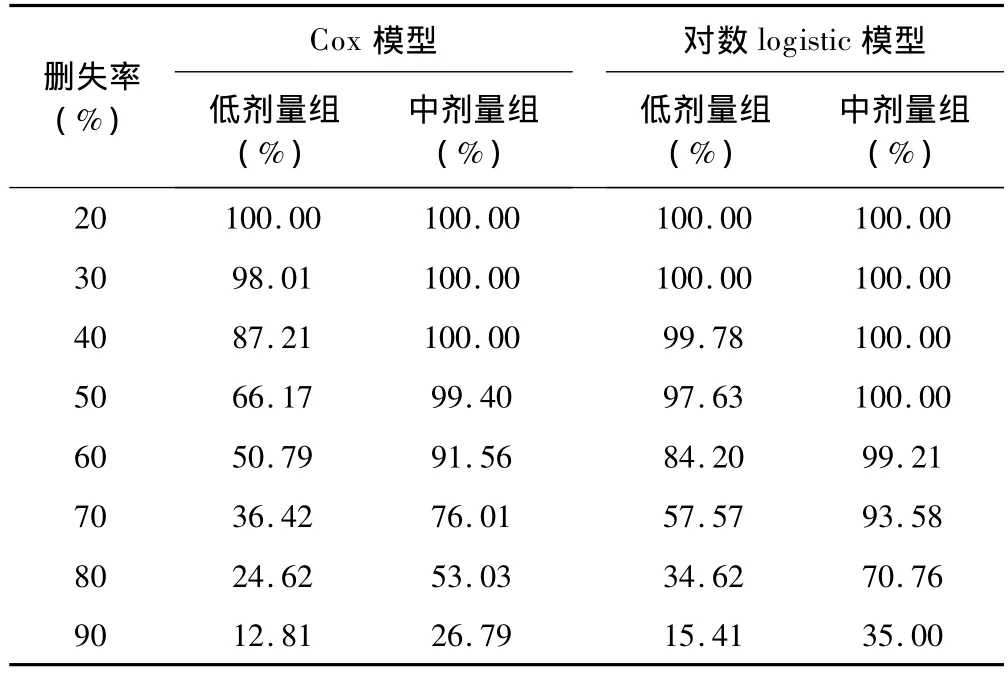
表3 不同删失率下Cox模型和对数logistic模型的有效性(power)比较

图1 不同样本量下Cox模型和对数logistic模型power的变化趋势

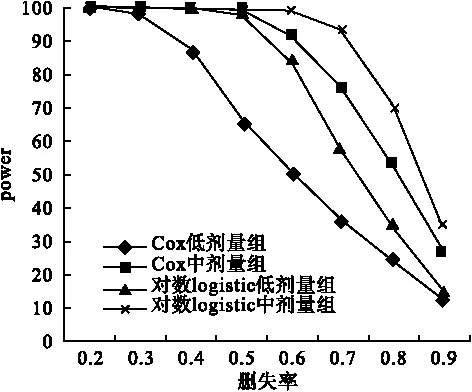
图2 不同删失率下Cox模型和对数logistic模型power的变化趋势

(2)偏倚性

由表4～5，图3～4可知，在不同样本量和删失率情况下，Cox模型的偏倚性均比对数logistic模型大。随着样本量的增加和删失率的降低，两模型的偏倚性逐渐减小。样本量不足200及或删失率超过70%时，偏倚性加速上升。

对于大样本(≥500)或删失率较小(≤30%)的数据，两类模型的偏倚性均较低，且差异较小。当样本量超过300或删失率小于60%时，对数logistic模型的偏倚性可控制在20%以内，但对于Cox模型，则要求样本量在400以上或删失率小于50%。

表4 不同样本量下Cox模型和对数logistic模型偏倚性的比较

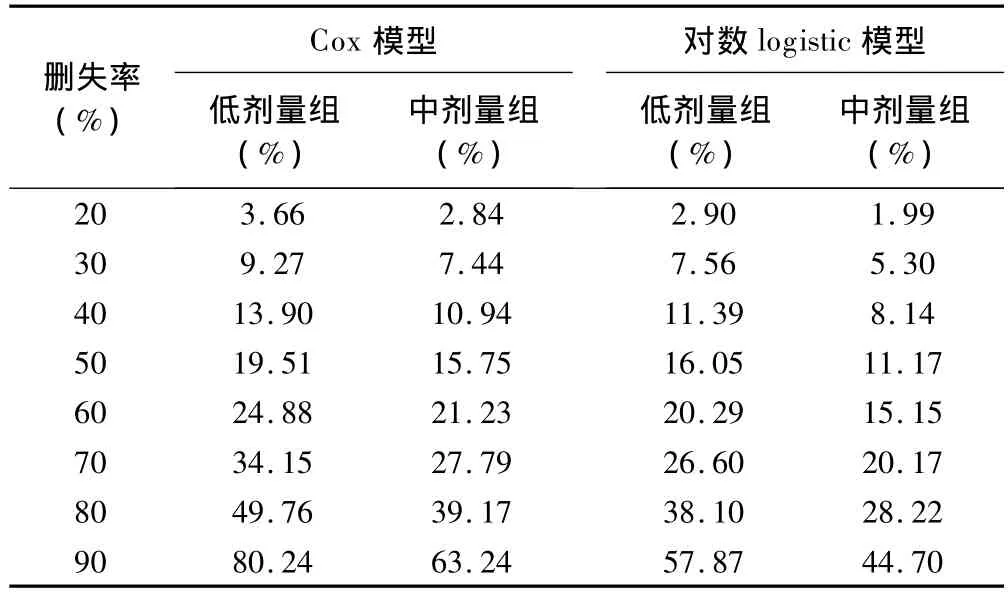
表5 不同删失率下Cox模型和对数logistic模型偏倚性的比较

图3 不同样本量下Cox模型和对数logistic模型bias的变化趋势

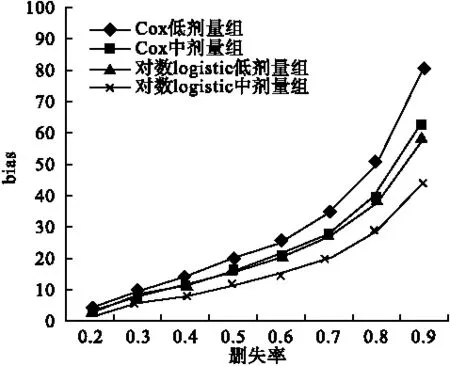
图4 不同删失率下Cox模型和对数logistic模型bias的变化趋势

讨 论

国外已有研究表明，利用实际数据进行模拟研究，进而探讨样本量和删失率对生存分析模型的影响是可行的〔8〕。本研究采取整群抽样，样本例数较多，随访时间长达3年半，大多数研究对象都发生了结局事件，删失率小于20%。因此，本研究将调查所得的全部受治者看做总体，通过完全随机的统计模拟，获得总体的无偏样本，保证了模拟样本参数估计值与总体参数估计值之间的可比性。

本研究的结果提示，对于生存时间服从某一特定分布类型的数据而言，在各种样本量和删失率下，Cox模型的有效性均较AFT模型低，即AFT模型的检验功效要优于Cox模型。随着样本量的减少和删失率的增高，两模型的有效性均下降，且Cox模型下降更为明显。当样本量分别低于300和400时，AFT模型和Cox模型的检验功效不足80%。

同样，在各种样本量和删失率下，Cox模型的偏倚性都较AFT模型大，即拟合良好的AFT模型的准确性比Cox模型更高，这与Cox等人的研究结果相一致〔9〕。两类模型的偏倚性均随样本量的增加以及删失率的降低而减小，但AFT模型偏倚性受样本量和删失率的影响小于Cox模型。

总体而言，对于大样本(≥500)或删失率较小(≤30%)的数据，Cox模型和AFT模型的有效性及偏倚性相近，分析结果均较为可靠。由于AFT模型需要先对生存时间的分布进行探索，分析过程较为繁琐，且医学研究中生存时间的分布往往很难确定〔10〕，此时Cox模型更加适用。但对于样本较小(300～400)或删失率较高(40% ～60%)的数据，AFT模型的分析结果更为可靠，此时应首先考虑采用该模型进行分析。但当样本量不足200或删失率超过70%时，两类模型的适用性都不佳。

1．方积乾，编著．生物医学研究中的统计方法．北京:高等教育出版社，2007，6．

2．Kay R，Kinnersley N．On the use of the accelerated failure time model as an alternative to the proportional hazards model in the treatment of time to event data:A case study in influenza．Drug Information Journal，2002，36(3):571-579．

3．叶展，顾杏元．Cox 模型及其讨论．中国卫生统计，1988，5(3):31-34．

4．Ward J，Wayne H，Mattick RP．Role of maintenance treatment in opioid dependence．The lanncet，1995，353(9148):221-226．

5．卫生部，公安部，国家药品监督管理局．海洛因成瘾者社区药物维持治疗试点工作暂行方案．北京，2003．

6．贾红英，王洁贞，赵敬杰．几种生存分析参数模型拟合方法及其应用．中国卫生统计，2004，21(4):102．

7．Health Canada．Best Practices-Methadone Maintenance Treatment．Ottawa，Her Majesty the Queen in Right of Canada，2002:

8．Orbe J，Ferreira E，Nú~nez-Antón V．Comparing proportional hazards and accelerated failure time models for survival analysis．Stat Med，2002，21(22):3493-3510．

9．Cox C，Chu HT，Schneider MF，et al．Parametric survival analysis and taxonomy of hazard functions for the generalized gamma distribution．．Statist．Med．，2007，26(23):4352-4374．

10．徐英，骆福添．生存分析中几种模型的研究概况．中国卫生统计，2006，23(4):364-366．