候诊成功率与候诊时间的非线性回归模型
2013-12-04浙江省杭州市萧山区中医院信息中心311201钟建亮唐立锋
浙江省杭州市萧山区中医院信息中心(311201) 钟建亮 孙 刚 唐立锋
门诊拥堵和次序混乱是各大小医院在诊疗活动中比较常见的现象。从事物的内在相关性的角度来讲,候诊成功率与候诊时间总是有着某种特定的函数关系。本文收集了某医院一个月候诊时间在7小时之内的全部门诊病人(共36697人)的候诊时间资料,来分析候诊成功率与候诊时间的关系,并利用SPSS统计分析软件建立两者之间的非线性回归模型,揭示两者之间的内在联系。
原理及回归模型的选择
logistic回归模型〔1-2〕用于反映二项分类因变量发生的概率(P)与其影响因素(X)之间的函数关系。候诊成功与否主要取决于候诊时间的长短。各时间段内累计候诊成功人数占总体门诊人数百分比为该时间段的候诊成功率。统计分析发现,候诊时间在整体候诊人群中并不是均匀的分布,也不符合正态分布,各时间段的候诊成功率与候诊时间的关系(图1)也证明两者之间存在着非线性回归关系,与logistic回归函数曲线非常类似。所以候诊成功率(P)与候诊时间(X)的函
数关系可假设为

实例分析
1.资料的收集与整理分析
资料来源于医院HIS系统数据库。本文所研究的候诊时间是指病人挂号后从排队候诊到成功就诊的时间差。通过分析与整理,以每10分钟为间隔,统计出各相应时段内累计候诊成功人数,见表1。

表1 候诊成功率与候诊时间分布关系表
2.统计分析及结果
选择SPSS软件logistic回归模型,添加α与β两个模型参数,初始值设为0,最大迭代次数选50次,平方和收敛性和参数收敛性均设1×10-8,结果如下:
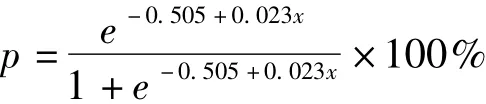
该回归方程决定系数为0.974,预测值为表1中PRED栏,预测值和实测值曲线如图1。预测值与实际值相近,模型有意义,回归方程拟合良好、有效。

图1 候诊成功率与候诊时间关系图
讨 论
近年来,“看病难”与“看病贵”成为了医院诊疗活动中一个突出的问题,其中“看病难”主要表现为病人门诊候诊时间过长。以候诊成功率作为因变量,以候诊时间作为自变量发现两者有一定的正相关性,候诊时间越长,候诊成功的概率越大。但是候诊成功率与候诊时间又不是一种简单的线性相关,即候诊时间的长短在整个候诊人群中并不是均衡的分布,所以用候诊时间的算术平均值来评价门诊的候诊情况是有缺陷的。logistic回归模型〔1-2〕是分析二分类因变量发生概率与其影响因素之间关系的函数模型,同样也适用于候诊成功率与候诊时间的关系分析,本文的实例分析也印证了该模型反映门诊候诊情况的科学性和有效性。在传统的非电子化的诊疗活动中,对于病人候诊时间数据的取得是不可能的,更无法研究候诊时间在候诊人群中的分布状况,而随着医院信息化建设的发展,各家医院HIS系统的应用,为候诊时间数据的取得和研究候诊时间在候诊人群中的分布提供了技术支持。候诊成功率与候诊时间函数模型的建立和分析,不但可以全面、科学、直观地反映候诊时间在候诊人群的分布情况,评价门诊候诊管理的优劣〔3-4〕,而且为合理地解决就诊高峰期,适时地增加门诊人员,科学地分流患者,缓解门诊拥堵的现象提供了有力的信息支持和科学依据,从而可以更好地提高门诊工作秩序,合理排班,改善门诊服务流程,进一完善门诊管理制度和门诊服务。
1.杨志雄,袁岱菁.非线性混合效应模型和广义线性模型拟和随机效应Logistic回归的应用比较.中国卫生统计,2011,28(3):321-323.
2.赵晋芳,罗天娥,范月玲.稀有事件Logistic回归在医学研究中的应用.中国卫生统计,2011,28(6):641-643.
3.王邰莉,樊俊青.浅谈基层医院门诊候诊大厅的管理.医学信息,2011,24(9):5643-5644.
4.徐波,危淑梅.二次分诊、二级候诊流程在门诊分诊排队系统中的应用.中国护理管理,2010,10(8):13-14.
