测井数据自适应多项式拟合去噪

2013-12-03蔡志东张固澜刘振亚

测井技术 2013年1期

蔡志东，张固澜，刘振亚

（东方地球物理公司新兴物探开发处，河北涿州072751）

0 引言

受到地层中随机噪声、井径大小、泥浆扰动和仪器自身等诸多因素的影响，测井资料中总是存在着不同程度的噪声。这些噪声在测井曲线上表现为许多与地层属性无关的统计起伏变化或是毛刺干扰［1］。测井曲线去噪通常采用曲线平滑、中值滤波、频率域低通滤波和小波变换等方法。

曲线平滑、中值滤波是直接、有效的高频噪声去除方法，但容易使测井曲线对地层属性的反映变模糊，降低属性界面的定位精度，影响了薄层和薄互层的识别能力；频率域滤波也是一种常用的去噪方法，通常采用低通滤波滤除高频噪声，但不利于局部属性细节分析［2］；小波变换被用于抑制测井数据噪声，可以有效地对白噪声进行去除，但是对于脉冲噪声的衰减有限，当噪声水平比较高时会使原始数据的高频端信号受到损伤［3］。以上几种方法都普遍应用于测井数据的去噪处理之中，但都是基于对测井曲线整体去噪处理的方法，不能有区别地对薄、厚层分别进行处理。真实的地层属性变化多种多样，同一口井所在的地层可能同时存在着大套的同属性介质、属性渐变的介质、薄层与薄互层介质等情况。本文以滑动多项式拟合法为基础，提出一种自适应改变多项式阶次进行测井曲线拟合的方法，通过统计窗口内样点值的变化规律，评估出最优多项式阶次，用该阶次多项式拟合窗口内的测井曲线，取拟合曲线的中点进行样点替换，然后向后移动一个样点重复上面过程，最终完成测井曲线拟合重构。

1 方法原理

假设采集测井记录用X（x）表示，噪声成分用S（x）表示，实际测井记录用Y（x）表示，则

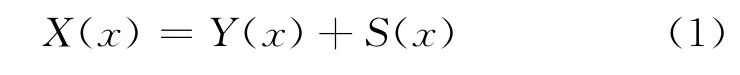
式中，x为测井记录中离散的数据样点。如果利用多项式对全部测井曲线Y（x）进行拟合，则

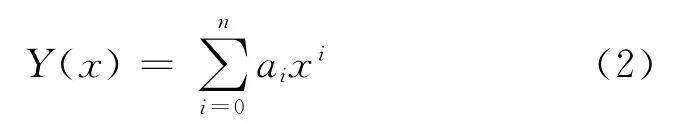
式中，n为多项式阶次，当n＝0时，Y（x）为常数a0，适合用来拟合属性不变的厚层；当n＝1，Y（x）适合用来拟合属性线性渐变的厚层；当n≥2时，Y（x）则可用来拟合属性非线性渐变的厚层、薄层和薄互层等，式（2）可以通过最小二乘法求得多项式Y（x）的系数ai。

当采用逐个样点连续滑动多项目式拟合时，以m表示滑动窗口内的样点数（为了使拟合数据中点对原数据中点的替换，约定m为奇数；程序实现时，如果判断m为偶数时将自动增加1个样点），则第j个m长度的窗口内拟合多项式为

式中，nj为第j个拟合多项式的阶次；l为测井数据记录的总样点数。该段拟合多项式的自由度vj为

为了阶次nj可以自适应判断选择，引入了卡方检验法，式（5）用来计算χ2值。

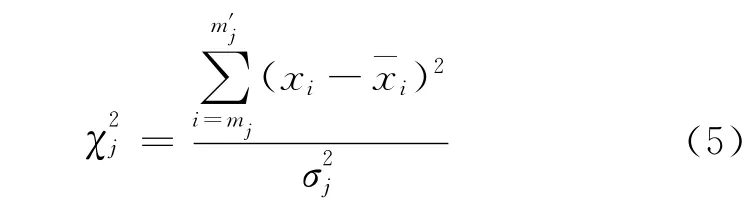
式中，mj和m′j分别为第j个m窗口的第1个和最后一个样点序号，均值则卡方检验函数为

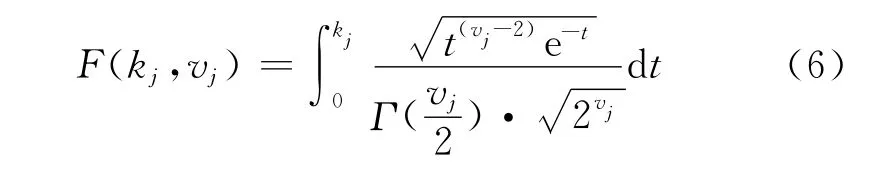
式中，Γ（z）为Γ函数，即用 Δj表示拟合的良好度，则

分别对第j个窗口内0阶到最高阶的拟合的良好度Δj进行对比判断，即可优选出nj，此时拟合多项式为Yj（x），当x＝xj时取到该多项式的中点Yj（xj），即可得到最终的拟合测井曲线为

式（8）中边界部分采用首尾多项式替换的方法，通过这种自适应多项式拟合的方法可以有区别地对薄层和厚层进行拟合，使测井曲线更能反映实际地层的属性。

2 仿真分析

2.1 仿真数据生成

根据上述理论，为了确定自适应多项式拟合测井曲线的参数和分析去噪效果，首先利用模型数据进行仿真试验。模型测井数据由随机变化的模拟测井曲线和随机噪声2种组分合成，数据采样间隔为0.1m、记录长度100m。图1（a）为模型数据的第1种组分随机噪声；图1（b）为模拟数据的第2种组分模拟测井曲线；图1（c）为由2种组分所合成的模型数据。

图1 模型数据的生成

2.2 拟合多项式的阶次范围

自适应滑动多项式拟合的最低拟合阶次为0阶，即允许利用常数直线拟合测井记录，这是与记录中同属性厚层的测井曲线特征相符合的；同时，也对最高拟合阶次进行了限制，如果阶次过高，不仅将影响计算效率，又可能对有效数据薄层识别造成伤害。

图2为随机截取的一段10m长的模型数据，利用0～10阶多项式分别进行拟合。结果表明，随着阶次的增大，拟合曲线的波动随之增强。

通过不同时长的数据进行测试，并结合实际数据处理经验和计算效率分析，认为以6～8阶为最高拟合阶次比较合适。

图2 模型数据（10m）不同阶次的多次项式拟合

2.3 拟合优良度门槛值的确定

拟合优良度门槛值是用来判断多项式拟合效果的一个临界值，用来自适应的优选多项式阶次，这个参数可以不进行设置，默认取优良度最好的阶次进行拟合。

如果给定了拟合优良度门槛值，当所有阶数的拟合优良度均不能满足该门槛值时，以优良度最高的阶次进行拟合，效果等同于未设置该参数；当只有1个阶次的拟合优良度高于这一门槛值时，就以这个阶次进行多项式拟合；当存在多个阶次同时满足门槛值时，将选择最低阶数的多项式拟合，这样既减少了计算量也更符合测井曲线的地球物理特征。

图2所示模型数据的拟合优良度如图3所示，随着拟合阶次的增加，拟合的优良度呈现递增趋势，建议该门槛值设置不小于80%。

2.4 窗口长度的确定

图3 模型数据（10m）不同阶次的拟合优良度

模型数据采样间隔为0.1m，如果要识别的薄层厚度为1m，假定拟合多项式的最高阶次可以取到8次，则窗口样点数最大可以取到70个，超过这一数值将影响薄层的识别效果；同时要保证对高频噪声的去除效果，窗口样点数也不能过小；通常选用与曲线平滑、中值滤波等计算方法相当或略大的窗口长度即可，建议窗口长度对应测井深度在1～5m之间，对于不同的测井数据，要根据具体情况在这一范围内进行多次实验确定最佳参数。

2.5 衰减结果分析

利用前面所分析确定的参数，对模型数据进行了去噪处理。图4（a）为自适应滑动多项式测井曲线拟合，显示了拟合过程中用到的不同阶次的所有多项式；图4（b）为原始测井数据和自适应拟合后的测井数据；图4（c）为拟合数据与合成前不含噪声数据的差值。处理结果表明，拟合效果较好，可以去噪还原得到较可靠的测井曲线，从残差结果看处理误差大多数在10%以内，可以验证该方法的有效性。

对于实际测井资料，为了获得最好的去噪效果，拟合多项式阶次范围、卡方检验优良度门槛值和窗口长度这3个参数在一定范围内可以适当地进行调整。

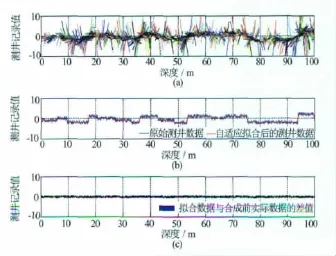
图4 模型数据的自适应滑动多项式拟合去噪

3 实际资料处理应用

3.1 原始测井数据分析

以土库曼斯坦巴格德雷地区1口井的测井资料为实例进行分析。该井区地层平缓、属性稳定，从录井资料分析，该井段主要以层状灰色泥岩为主，夹着多套厚度不大于5m的浅灰色粉砂岩薄层。图5（a）为原始自然伽马测井曲线，数据的噪声水平较高，需要经过去噪处理才能反映较真实的地层属性。

图5 实际测井资料的各种去噪方法对比

3.2 常规去噪效果

图5（b）、图5（c）和图5（d）是分别采用了移动平均平滑、中值滤波、频率域低通滤波等3种方法去噪得到的处理结果，3种方法均能达到一定的高频噪声去除效果。综合对比3种方法，移动平均光滑效果不如其他2种方法；中值滤波法的较厚地层属性界面略清晰，但薄层反映不明显；频率域低通滤波法的对薄层有一定反映，但地层属性界面却较不清晰。