基于小波变换的指纹图像增强算法

孙勤江 （中海石油 （中国）有限公司天津分公司工程建设部，天津300452）

雷 声 （中国石油天然气管道局天津设计院，天津300457）

陈建玲 （中海油能源发展股份有限公司油田建设工程设计研发中心，天津300452）

随着计算机和网络的迅速发展，基于生物特征识别的智能身份认证技术正受到越来越多的关注。由于指纹识别技术是生物识别领域技术中最成熟的一门应用技术，使得指纹识别成为目前应用最广泛、可信度最高的个人身份认证技术之一。指纹图像增强是一个改善指纹图像纹理特征的过程。在指纹识别流程中图像增强是一个重要的步骤，通过图像增强可以获得高质量的指纹图像，使提取特征点时获得的细节信息更为精确［1－2］。然而，在实际应用中，指纹图像不可能总是拥有很好的质量，噪声的干扰会破坏脊线的结构。这种脊线结构的损坏可能会由如下原因引起：皮肤疤痕、空气湿度、灰尘和指纹与录入器的非均匀接触。指纹图像中的噪声可以分为几种不同的类型：指纹的折痕，皱纹和表皮受损。

在指纹匹配之前，必须消除这些噪声，恢复指纹脊线结构。为了改善指纹的脊线结构，需要使用一些指纹增强算法。在增强过程中的方法或算法必须很好地适应指纹的纹理特性，产生良好的处理结果。在图像增强领域，比较经典的方法是小波变换，它通过高通滤波器对图像进行滤波，然后与原图叠加，该算法具有简单易用的特点［3－4］。但是它在对图像进行增强处理的过程中也对图像中存在的噪声做了同样的处理，在增强图像边缘细节的同时没有很好的进行图像消噪。针对这些不足，笔者对传统的小波变换算法进行了改进。

1 传统的小波变换图像增强算法

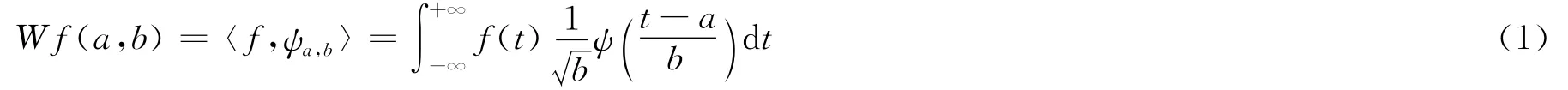
小波函数的定义域很小，在定义域之外，函数值、平均值和ψ（t）的高阶矩阵均为0，即：

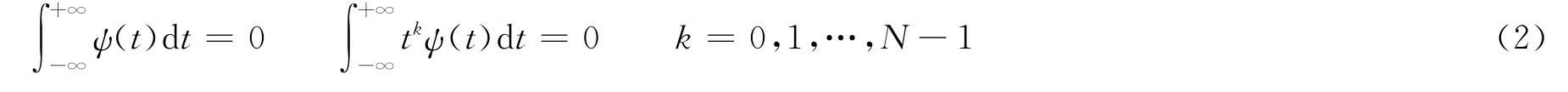
小波的容许条件即是均值为0的条件。

小波函数集中的一系列函数均是由ψ（t）经平移和伸缩得来，设j和k分别为收缩和平移参数，则有：小波的宽度随着j的变化而变化，平移位置则由k决定。

在数字图像处理中，数据以离散的形式表示，基于离散数据的小波变换是在一定的规则下，对连续小波变换进行采样。因此离散小波变换一般具备连续小波变换的性质。

设Vj，Wj分别是小波函数集φj，k（t），ψj，k（t）的正交基，则Vj－1空间下的正交基可表示为：Vj－1＝Vj⊕Wj，j∈Z，由此式可得V0空间下的小波分解：

可以通过式（3）使用一对低通和高通滤波器h和g实现小波变换在相邻尺度空间的分解和重构，使输入信号在小波域分解成逼近于细节空间的信号。通常的做法是对图像在小波域上进行分解：

式中，a，b代表图像的坐标值；Fhp（a，b）代表高频分量；Flp（a，b）代表低频分量。设有低通滤波器［5］的传输函数 Hlp（a，b），则有：

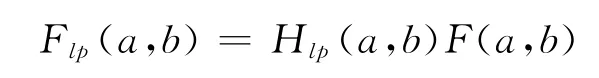
因此，在频域角度基于小波变换的图像增强可用滤波器的合成实现：

基于小波变换的图像增强算法的实质就是将图像在频域上进行小波分解，得到图像中的高频分量和低频分量，再将图像中的低频分量去除，在原图上叠加一个或数个经处理得到的高频分量，高频滤波器的传输函数一般可表示为：

这种基于小波变换的图像增强算法虽然在图像增强方面有较好的效果，但是在增强图像的同时，会放大图像中的噪声，使图像的特征信息质量变差。

2 基于Mallat算法对小波函数的改进

针对传统小波变换在图像处理中计算量大、增强图像的同时会放大噪声的缺点，笔者使用Mallat算法对小波进行分解和重构，使用非线性算子对图像高频部分进行增强。Mallat算法［6］是把多分辨率的概念［7］、滤波器族［8］、金字塔编码策略［9］等思想结合在一起所形成的，是数字信号处理领域进行小波变换分析的基础。Mallat算法假定已经计算出函数f（t）在分辨率2j下的离散逼近Ajf（t），可以通过离散低通滤波器对Ajf（t）进行滤波得到f（t）在2j＋1分辨率下的逼近Aj＋1f（t）。

首先需要在一维空间中使用Mallat算法做小波分解。设函数f（t）∈l2（R）在定义域内可积，对函数f（t）进行基于低通平滑函数φ（t）的平滑运算，并把这个计算过程看做为一种在极限情况下的逼近，在逐级逼近的过程中，低通平滑函数φ（t）也在进行伸缩，这样就实现了在不同分辨率下对f（t）进行逐级逼近，这就是多分辨率的思想。在分析图像信息时，基于多分辨率的分析非常有效。具体算法如下：

设φj（t），ψj（t）分别为信号函数f（t）在2j分辨率下的尺度函数和小波函数，φj，k（t）为空间Vj中的正交基，Vj中任意函数Ajf（t）可表示为φj，k（t），k∈Z 的线性组合。

在Vj中，有信号函数f（t）的平滑逼近Ajf（t）和细节函数Djf（t）：

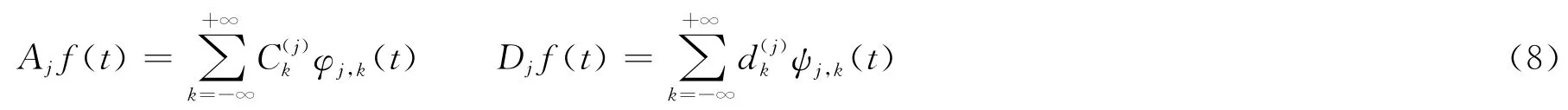
根据多分辨率函数空间的分解思想，Ajf（t）分解为：

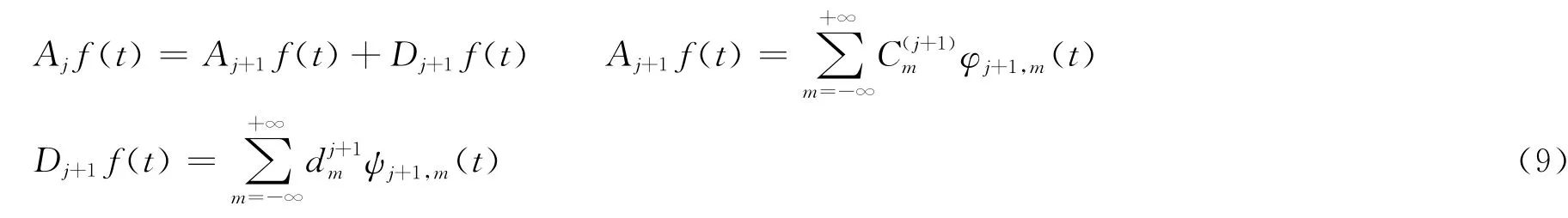
式（9）为信号函数的一级逼近，在此基础上进行同样的操作得到信号函数的二级逼近：

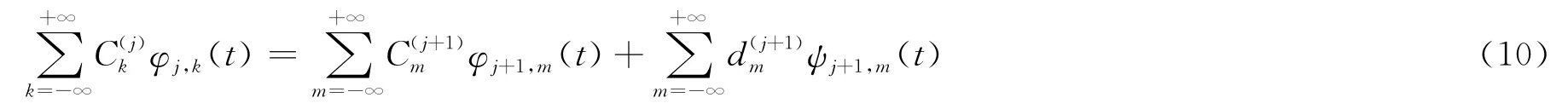
分解算法推导完毕，同理可推导出重构算法，首先进行基于二叉树结构的滤波和信息抽取：

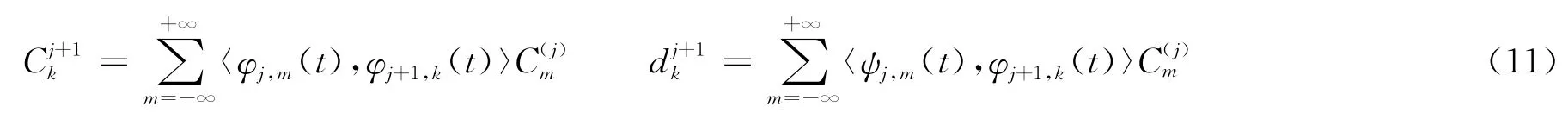
所以得到非线性变换函数：

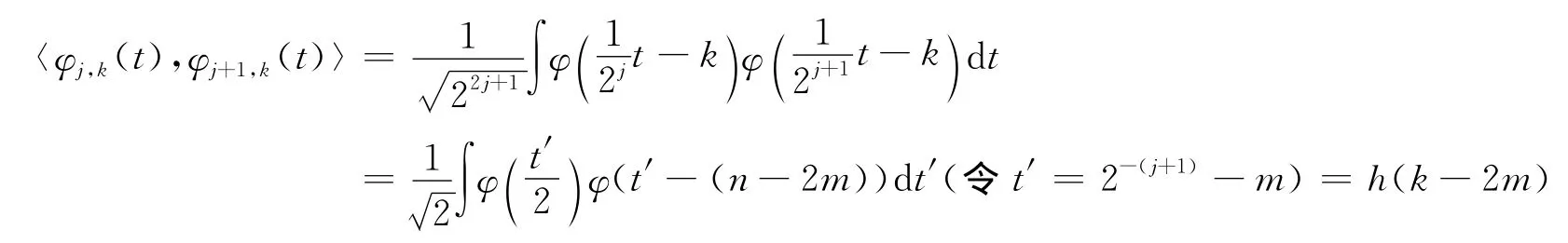
同理可得：

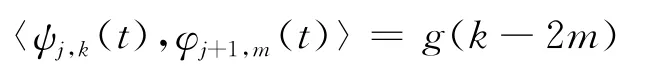
使用非线性函数对式（11）推导可得：

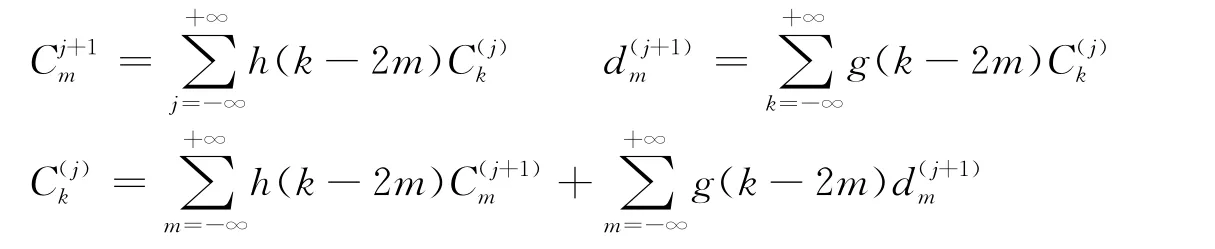
改进后的算法实质是在小波分解过程中，对原始信号进行基于二叉树结构［10］的滤波和信息抽取［11］，得到离散平滑逼近和离散细节逼近，并定义为第一级的逼近，然后再在第一级的离散平滑逼近基础上进行同样的操作得到二级逼近。逐级进行操作后可以得到各级的离散细节逼近，并作为各级的小波系数。在对信号进行重构时，则进行反向操作，并将抽取运算变为插值［12－13］运算。在逐级分解的过程中得到了各级的高频分量，在逐级重构中，使用了非线性函数对图像高频区域进行了增强，实现了对噪声的去除和图像的增强。

图1 算法效果对比

3 指纹识别试验

对图像进行小波分解，得到一副N×N大小的图像，用Mallat算法分解为4幅大小的子图像，对子图像中含有高频分量的区域应用非线性函数进行增强，再重构回原指纹图像，增强处理完毕。

为了使传统小波变换增强算法与改进后的算法进行对比。在内存为2G、主频为2.4G双核的PC机上进行算法测试，指纹图像为256像素×256像素的8位灰度图。算法的识别效果图如图1所示。图1（a）为原始图像，图1（b）为传统小波变换算法的处理效果，图1（c）为改进后的算法处理效果，通过几幅图像的比较可以得出，传统小波变换算法在图像高频部分的去噪处理不佳，部分区域产生了毛刺，而改进后的算法既能有效地增强图像，又在局部很好的抑制了噪声的影响。

4 结 语

基于Mallat函数，从多分辨率的概念、滤波器族、金字塔编码策略相结合的角度对小波函数进行了改进，使用非线性算子对图像的含有高频分量的部分进行边缘增强，然后重构回原指纹图像。从指纹识别结果来看，传统小波变换的算法在对图像进行增强的同时也放大了噪声，笔者所设计的算法比指纹增强的经典算法的边缘增强效果有一定程度的提高，能够在增强边缘的同时有效地抑制噪声。

［1］柴小光，岑宝炽 .民用指纹识别技术 ［M］.北京：人民邮电出版社，2004.

［2］Jain A K，Hong L，Pankanti S，et al.An Identity Authentication System using Fingerprints［J］.Proceedings of the IEEE，1997，85 （9）：1365－1388.

［3］Xiao Q，Raafa H.Fingerprint image Post Proeessing：a combined statistical and structural approach ［J］.Pattern Reeognition，1991，24 （10）：895－992.

［4］Moayer B，Fu K S.A Syntactic Approach to Fingerprint Pattern Recognition ［J］.Pattern Recognition，1975，6：65－68.

［5］徐建华 .图像处理与分析 ［M］.北京：科学出版社，1992.

［6］He Yu－liang，Tian Jie，Luo Xi－ping.Image Enhancement and Minutiae Matching in Finger－print Verification ［J］.Pattern Recognition Letters，2003，24 （9）：1349－1365.

［7］Clarke R.Human Identification Information Systems： Management Challenges and Public Policy Issues ［J］.Information Technology＆People，1994，7 （4）：6－37.

［8］Nalla V.Automatic online signature verification ［J］.Proceedings of IEEE，1997，85 （2）：213－239.

［9］Jain A，Hong L，Boole R.On－Line Fingerprint Verification ［J］.IEEE Pattern Analysis and Machine Intelligence，1997，19 （4）：302－311.

［10］Gonzales R C，Woods R E.Digital Image Processing ［M］.New York：Addison－Wesley，1993.

［11］林国清，李见为，王崇文 .指纹图像的预处理 ［J］.计算机工程，2002，28（9）：171－172.

［12］朱志刚，林学言，石定机，等 .数字图像处理 ［M］.北京：电子工业出版社，2002：23－25.

［13］倪林，张长水，荣钢，等 .基于快速对称小波变换的高效模糊指纹图象压缩方法 ［J］.软件学报，1996，7（5）：272－278.