两类相依样本密度函数核估计的相合性

胡 学 平

(安庆师范学院 数学与计算科学学院,安徽 安庆 246133)

0 引言与预备知识

概率密度估计在数理统计中应用广泛,概率密度估计方法很多,如直方图估计、Rosenblatt法[1]、Parzen估计[2]以及最邻近估计[3]等.文献[3-6]讨论了独立同分布随机样本和一些相依随机样本密度函数的核估计,获得了其相合性、收敛速度及渐近正态性等性质.此外,相依序列的极限理论在金融数学、生存数据以及水文、电力系统等领域应用广泛.Joag-Dev等[7]引入了NOD(negatively orthant dependent)概念,并指出任何NA列都是NOD的,并给出了一个是NOD但不是NA的实例,即NOD是严格弱于NA的.本文在NOD样本和m相依[8]样本下分别进一步探讨概率密度函数核估计的性质,获得了核估计的强相合性、r阶相合性及依概率一致收敛性,推广并改进了文献[5-6]的相关结论.本文约定C表示正常数,在不同处取不同值.

引理1[3]设K(u)和g(x)都是定义在(-∞,∞)上的Borel可测函数,满足下列条件:

1)K在(-∞,∞)上有界;

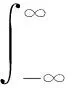
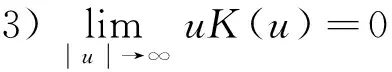
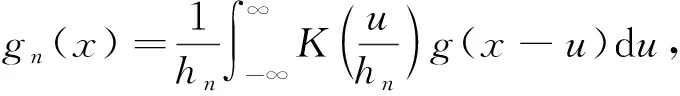
(1)

又若g在(-∞,∞)上有界且一致连续,则

(2)

引理2[9]设随机变量序列X1,…,Xn为NOD的,f1,…,fn均为非降函数(或非增函数),则随机变量f1(X1),…,fn(Xn)仍为NOD的.

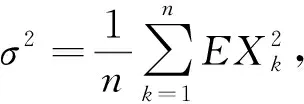
证明：易验证∀x∈1有ex≤1+x+x2e|x|/2,从而对t>0,根据条件|Xk|≤an和EXk=0,可得

(3)

再利用引理2、引理3及式(3)可得

(4)

结合Markov不等式和式(4)有

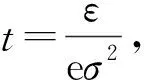
1 主要结果

定理1设{Xn,n≥1}为同分布的NOD随机变量序列,K(u)为有界变差概率密度函数.如果:

1)

(5)

2) 密度函数f(x)在(-∞,∞)上有界或

(6)

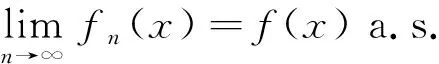
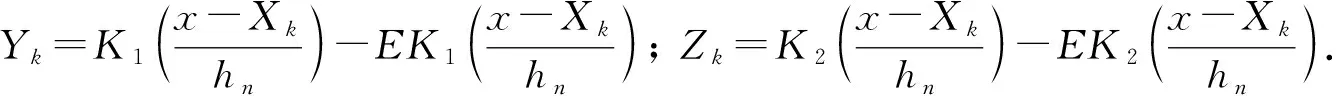
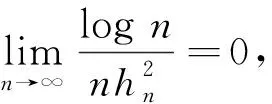
同理可证

根据Borel-Cantelli引理可知结论成立.

证明:根据Cr-不等式,有

结合定理1的证明过程、Cr-不等式及引理4可得

对r∈(0,2],利用Jensen不等式可得

注1定理1和定理2减弱了文献[6]中相应定理的条件,且推广到更广泛的NOD随机样本情形.

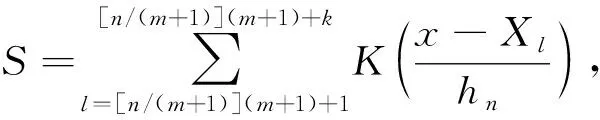
从而只需证明Ik→0,k=1,2.对于I1,有

易证若K(u)满足引理1的条件,则K2(u)也满足,因此根据式(1)可得

利用Jensen不等式,对r∈(0,2],有

定理4设{Xn,n≥1}为严平稳的m相依随机序列,K(u)为概率密度函数.如果满足下列条件:

2) 密度函数f(x)在(-∞,∞)上一致连续;

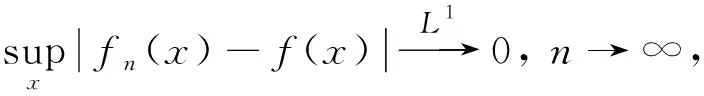
证明:沿用定理3的记号,有

由条件3)和反演公式得

(8)

[1] Rosenblatt M.Remarks on Some Nonparametric Estimates of a Density Function [J].Ann Math Statist,1956,27(3):832-837.

[2] Parzen E.On Estimation of a Probability Density Function and Mode [J].Ann Math Statist,1962,33(3):1065-1076.

[3] 陈希孺,方兆本,李国英,等.非参数统计 [M].上海:上海科技出版社,1989.

[4] LIU Yong-hui,WU Qun-ying.Consistency of Nearest Neighbor Estimator of Density Function for Negatively Dependent Samples [J].Journal of Jilin University:Science Edition,2012,50(6):1141-1145.(刘永辉,吴群英.ND样本最邻近密度估计的相合性 [J].吉林大学学报:理学版,2012,50(6):1141-1145.)

[5] YU Zhuo-xi,DONG Zhi-shan,WANG De-hui.Consistency for the Kernel-Type Density Estimator in the Case ofm-Dependent Samples [J].Journal of Jilin University:Science Edition,2007,45(4):507-510.(于卓熙,董志山,王德辉.m相依样本概率密度函数核估计的相合性 [J].吉林大学学报:理学版,2007,45(4):507-510.)

[6] WEI Lai-sheng.The Consistencies for the Kernel-Type Density Estimator in the Case of NA Samples [J].Journal of Systems Science and Mathematical Sciences,2001,21(1):79-87.(韦来生.NA样本概率密度函数核估计的相合性 [J].系统科学与数学,2001,21(1):79-87.)

[7] Joag-Dev K,Proschan F.Negative Association of Random Variables with Applications [J].Ann Statist,1983,11(1):286-295.

[8] Chung K L.A Course in Probability Theory [M].New York:Academic Press,1974.

[9] Bozorgnia A,Patterson R F,Taylor R L.Limit Theorems for Dependent Random Variables [C]//Proceedings of the First World Congress on World Congress of Nonlinear Analysts.Hawthorne:Walter de Grutyer &Co,1996:1639-1650.

[10] Kim H C.The Hjek-Rényi Inequality for Weighted Sums of Negatively Orthant Dependent Random Variables [J].Int J Contemp Math Sci,2006,1(6):297-303.