基于数理统计基因识别问题的研究
2013-12-03王璐
王 璐
(西安建筑科技大学理学院数学系 陕西西安 710055)
随着人类基因组计划的完成,生物基因数据呈指数形式增长,找出蛋白质编码基因,是进行基因组分析的基础,在生物信息处理中占有非常重要的地位[1].通常的基因识别方法大致可以分为如下3类:序列相似性方法、从头预测方法、序列相似性和从头预测方法相结合的第三类方法[2].由于物种的多样性,生物基因数据的指数型增长和人类对其有限的认识等原因,第一类方法的缺陷不仅速度较慢,而且准确率不高.相较第一类来说,第二类方法具有更坚实的数学基础,模型的物理意义也更加明显直观,而且,在实验当中对若干基因预测软件的测试表明,具有最高正确率的几种基因预测软件都属于这一种方法[1].
在生物学、医学、药学等诸多方面,DNA的研究都具有重要的理论意义和实际价值[3].在面对大量、复杂的基因序列数据时,如何更好更快捷地获取准确的基因信息,如何能够在众多的基因序列中确定功率谱和信噪比,如何能够对每类基因快速地得到其阈值确定方法,如何快速实现基因识别算法,是摆在我们面前的一个具有研究意义的实际课题.
本文将以现有的基因序列数据为研究对象研究基因识别的系统建模方法和相关理论算法,研究基因识别模型的建立或改进方法,通过统计分析的相关方法研究基因特征的识别,并通过计算机手段进行实现.在基因识别问题研究中,首先研究基因识别问题的特征,从而研究编码蛋白质的基因识别方法,进而针对生物必需基因识别的问题进行研究[2].本文在使用已有模型算法并辅助实现相应模型的过程中,对已有的方法进行深入分析和比较,找出各方法的不足和长处,发现新问题,提出更有效的解决方法,使其与已有算法互相融合,取长补短,促进其在实践中的应用[2].在对各经典算法及相关模型掌握的基础上,运用所学的统计分析方法建立数学模型,并运用数据处理软件对数据进行预处理、编程并求解模型,并对研究的数据进行特征提取和识别.针对外显子和内含子序列片段的功率谱表现不同的特性,研究相应的算法,以实现外显子片段的提取和识别[4].
1 基于Voss 映射求解功率谱和信噪比方法
1.1 Voss 映射
z这是指将同一类信号从长串的信号序列中单独分离出来,并保持其在长序列中的相应位置不变.
在DNA序列研究中,首先需要把A、T、G、C4种核苷酸的符号序列,根据一定的规则映射成相应的数值序列,以便于对其作数字处理[3].
令I={A,T,G,C},长度为N的任意DNA序列,可表达为
S={S[n]|S[n]I,n=0,1,2,…N-1}
即A、T、G、C的符号序列S:S[0],S[1],…,S[N-1].现对于任意确定的bI,
Voss映射的关系式为:
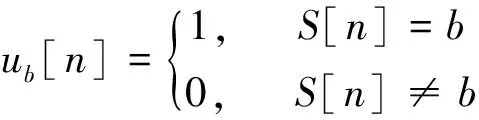
称之为Voss映射,于是生成相应的0-1序列(即二进制序列){ub[n]}:ub[0],ub[1],…,ub[N-1](bI).
1.2 傅里叶变换方法
假设给定的一段DNA序列片段为S = ATCGTACTG,则所生成的4个0-1序列分别为[4]:
{uA[n]}:{1,0,0,0,0,1,0,0,0};{uG[n]}:{0,0,0,1,0,0,0,0,1};
{uC[n]}:{0,0,1,0,0,0,1,0,0};{uT[n]}:{0,1,0,0,1,0,0,1,0}。
这样产生的四个数字序列又称为DNA序列的指示序列.为研究DNA编码序列(外显子)的特性,对指示序列分别做离散Fourier 变换(DFT)[3].
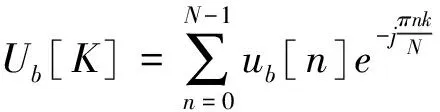
以此可得到4个长度均为N的复数序列{Ub[K]},bI.
1.3 功率谱与信噪比
计算每个复序列{Ub[K]}的平方功率谱,并相加则得到整个DNA序列S的功率谱序列{P[K]}[4]:
P[K]=|UA[K]|2+|UT[K]|2+|UG[K]|2+|UC[K]|2,k=0,1,…N-1
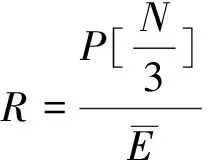
笔者采用了附件中的genes6中的数据,基因长度n=5800,运行第1行第1列的基因数据,计算机主程序如下所示:
clear all;
load genes6.mat;
gene=genes(1,1).Seq;
n=length(gene);
%生成A的指示序列uA[n]
for i=1:n
if strcmp(′A′,gene(i))
ua(i)=1;
else ua(i)=0;
end
end
%生成G的指示序列uG[n]
for i=1:n
if strcmp(′G′,gene(i))
ug(i)=1;
else ug(i)=0;
end
end
%生成C的指示序列uC[n]
for i=1:n
if strcmp(′C′,gene(i))
uc(i)=1;
else uc(i)=0;
end
end
%生成T的指示序列uT[n]
for i=1:n
if strcmp('T',gene(i))
ut(i)=1;
else ut(i)=0;
end
end
fua=fft(ua,n);
fug=fft(ug,n);
fuc=fft(uc,n);
fut=fft(ut,n);
for k=1:n
p(k)=abs(fua(k))^2+abs(fug(k))^2+abs(fuc(k))^2+abs(fut(k))^2;
end
plot(p(floor(n/100):n))
e=sum(p)/n
p1=[p(round(n/3)-2),p(round(n/3)-1),p(round(n/3)),p(round(n/3)+1),p(round(n/3)+2)〗;
pn3=max(p1);
r=pn3/e
r=3.4474
通过运行计算机程序,得到下列结果:
e=5.8000e+003
r=3.4474
所以笔者认为:DNA序列genes6的总功率谱的平均值为e=5.8000e+003,信噪比r=3.4474.
2 基于Z-curve 映射求解功率谱与信噪比方法
设DNA序列S的4个指示序列{ub[n]},bI={A,C,G,T},n=0,1,2,…N-1的累积序列bn(n=0,1,…,N-1)为.则定义3个序列 :x[n],y[n],z[n]:
令x[-1]=0,y[-1]=0和z[-1]=0,以及Δx[n]=x[n]-x[n-1],
Δy[n]=y[n]-y[n-1]和Δz[n]=z[n]-z[n-1],于是得到Z-curve映射:
例如,对DNA序列S(n):ACGTTAG,则对应的Z-curve映射序列为:
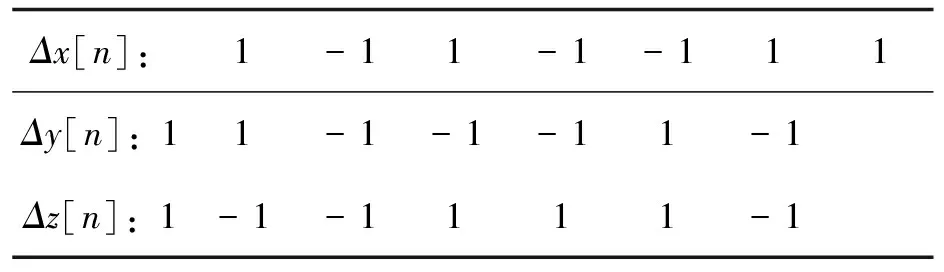
Δx[n]:1-11-1-111Δy[n]:11-1-1-11-1Δz[n]:1-1-1111-1
类似于Voss 映射那样,定义Z-curve映射的总功率谱,
PZ[k]=|ΔX[k]|2+|ΔY[k]|2+|ΔZ[k]|2,
其中ΔX[k],ΔY[k]和ΔZ[k]分别表示数字序列Δx[n],Δy[n]和Δz[n]的离散傅里叶变换.
定义Z-curve映射的信噪比为:
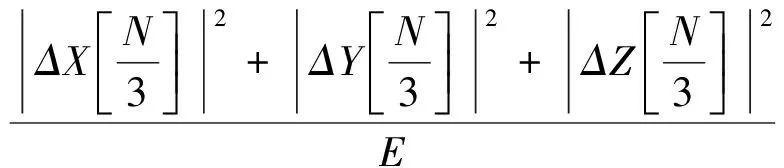
笔者采用了附件中的genes6中的数据,基因长度n=5800,运行任意给定的的基因数据,计算机主程序运算结果如下:
clear all;
Load genes6.mat;
gene=genes(1,1).Seq;
n=length(gene);
%生成A的指示序列uA[n]
for i=1:n
if strcmp(‘A’,gene(i))
ua(i)=1;
else ua(i)=0;
end
end
%生成G的指示序列uG[n]
for i=1:n
if strcmp(‘G’,gene(i))
ug(i)=1;
else ug(i)=0;
end
end
%生成C的指示序列uC[n]
for i=1:n
if strcmp(‘C’,gene(i))
uc(i)=1;
else uc(i)=0;
end
end
%生成T的指示序列uT[n]
for i=1:n
if strcmp(‘T’,gene(i))
ut(i)=1;
else ut(i)=0;
end
end
a=[1,-1,1,-1;1,1,-1,-1;1,-1,-1,1];
dxyz=a*[ua;uc;ug;ut];
fdx=fft(dxyz(1,:),n);
fdy=fft(dxyz(2,:),n);
fdz=fft(dxyz(3,:),n);
for k=1:n
p(k)=ads(fdx(k))^2+abs(fdy(k))^2+abs(fdz(k))^2;
end
plot(p(floor(n/100):n))
>>e=sum(p)/n
e=1.7400e+004
>>pl=[p(round(n/3)-2),p(round(n/3)-1),p(round(n/3),p(round(n/3)+1),p(round(n/3)+2)];
pn3=max(p1);
r=4.5965
通过运行计算机程序,我们得到下列结果:
e=1.7400e+004
r=4.5965
所以笔者认为:DNA序列genes6的总功率谱的平均值为e=1.7400e+004,信噪比r=4.5965.
3 基因识别算法的实现
在此笔者采用的是基于固定长度滑动窗口上频谱曲线的基因识别方法,对一个DNA序列S和它的指示序列{ub[n]}[3],bI,n=0,1,2,…,N-1.取长度M(通常取为3的倍数)作为固定窗口长度.
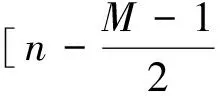
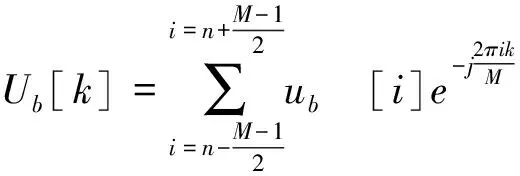
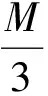
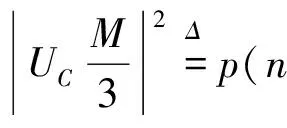
图1是运行Voss 映射程序的第1行第1列数据所得到的频谱图,其R值为R=3.4474.
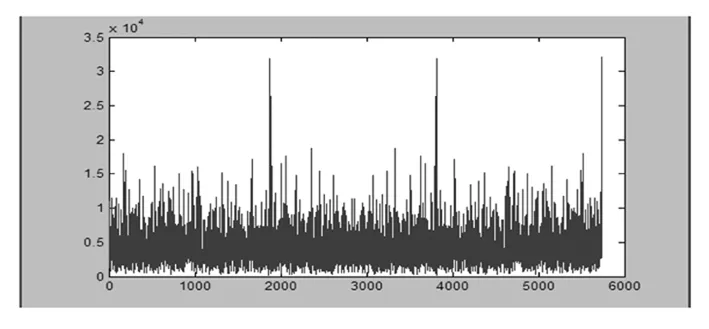
图1 Genes6 的第一段基因序列的频谱图
从图1可以看到,该频谱图呈现较为明显的3-周期性,大致在2000、4000和6000处出现峰值.
为探究某片段是否为具有三周期性的外显子基因,笔者截取片段上的一部分,图2为附件1第一段基因序列中3—120处的频谱图.
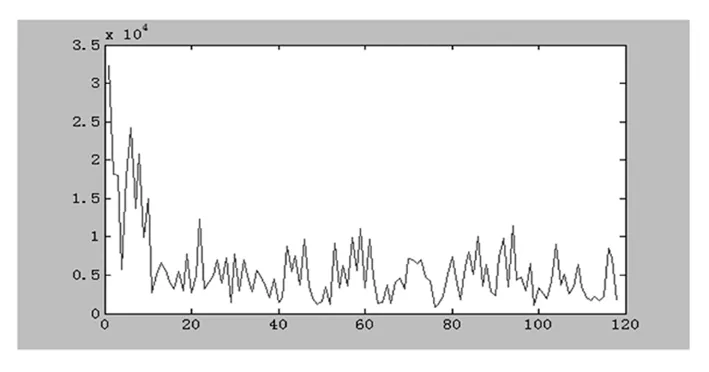
图2 Genes6第一段基因序列中取值(3——120)
通过图像,首先去掉开始部分未形成规律性的频谱.然后选取最大值处,设此处为n1/3(在此我们选取48),此处为该段中的第一个峰值,再继续寻找峰值n2/3(60),比较前两个峰值处的值是否相近,若相近,则笔者断定该处形成了三周期性.利用基因的三周期性,判别处该段为外显子,此段长度为234.同理,利用此方法,寻找其他外显子区域.两个外显子之间即为内含子,由此得出外显子的两个端点(36和72).实现了对基因的识别.
图2是运行Genes6第1行第2列数据所得到的频谱图,得到R值为R=1.3827.笔者可以看到图2在整段上不具有3-周期性,但是从局部上来看部分段具有3-周期性.
图3为150—480段处的频谱图,利用上面的分析方法,同样可以得到很多段外显子和内含子的区间,由此可以实现对基因的判别.
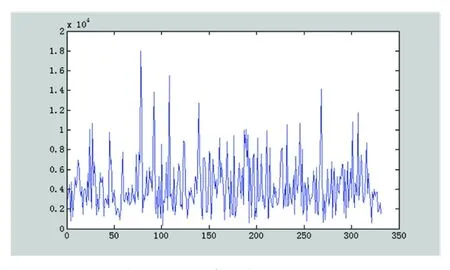
图3 Genes6第一段基因序列中取值(150—480)
图3是运行Genes6第1行第3列数据所得到的频谱图,得到R值为R=1.2524.笔者可以看到图3在整段上不具有3-周期性,噪声较大,因此笔者认为此段不具有外显性.
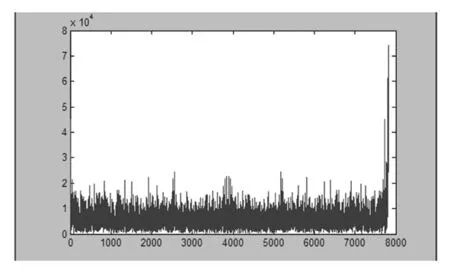
图4 Genes6 的第二段基因序列的频谱图
图4是运行Genes6第1行第4列数据所得到的频谱图,得到R值为R=3.5113.笔者可以看到图4在整段上不具有3-周期性,噪声太大,因此笔者认为此段不具有外显性.
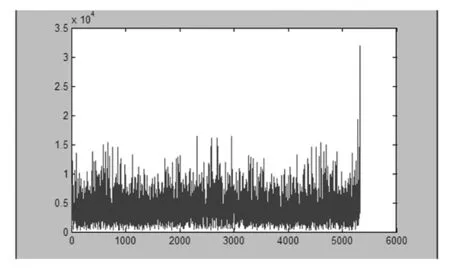
图5 Genes6 的第三段基因序列的频谱图
图5是运行Genes6第1行第5列数据所得到的频谱图,得到R值为R=2.4334.此段上R值数值较大,在整段上3-周期性不是很明显,但是局部存在3-周期性的可能。因此笔者初步认为此段可能存在外显性.
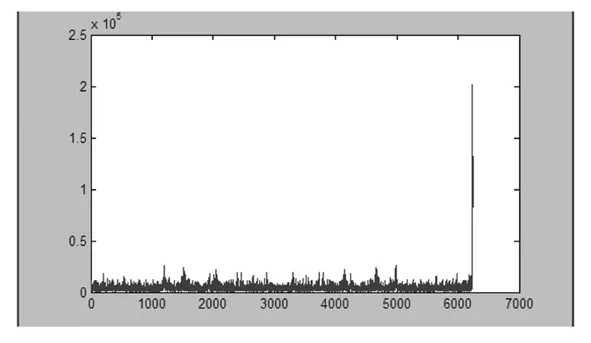
图6 Genes6 的第四段基因序列的频谱图
图6是运行Genes6第1行第6列数据所得到的频谱图,得到R值为R=0.9958.在整段上3-周期性不是很明显,但是局部存在3-周期性的可能.因此笔者初步认为此段可能存在外显性。
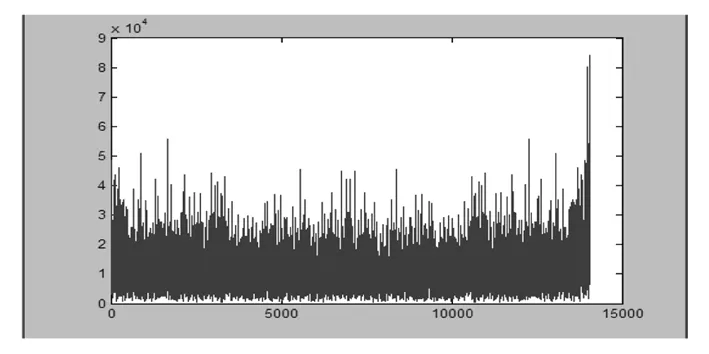
图7 Genes6 的第五段基因序列的频谱图
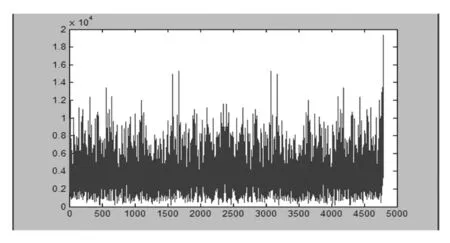
图8 Genes6 的第六段基因序列的频谱图
4 结论
本文在了解基因存在及其构成的基础上,运用核苷酸的非平衡性和快速Fourier 变换等方法求取功率谱和信噪比,得到理想准确的基因序列.
为了检验所得数据的有效性,Voss映射和Z-curve 映射进行再次分析.通过分析与比较,笔者发现基于Voss映射和Z-curve 映射运算的信噪比二者呈现一定的常数倍数关系,大约为1.3333.因此,笔者认为Z-curve 映射比Voss映射更具有生物学意义.
参考文献:
[1]杨莉.DNA序列4D表示及基因识别算法研究[D].长沙:湖南大学,2007.11.
[2]周柚.基因识别和微阵列数据识别算法研究[D].长春:吉林大学,2008.4.
[3]2012研究生数模式题[EB/OL].百度文库,http//wenku.baidu.com/view/bde7341552d380
ebb2946d91.html.
[4]方芷君,明媚,王婷,等.基因预测中的信噪e计算问题[C].桂林:广西计算机学会2012年学术会议论文集.2012.
