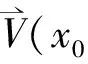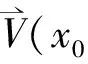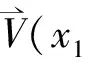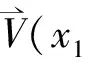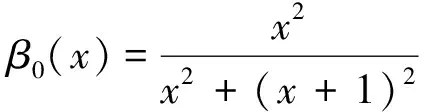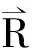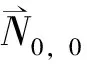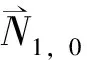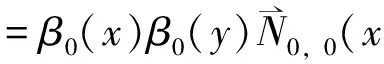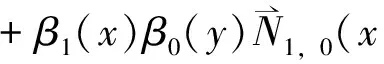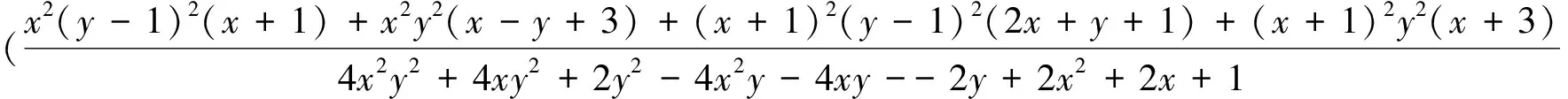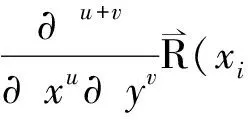向量值有理插值的构造方法*
2013-12-03马锦锦
马锦锦
(安徽建筑大学数理系 安徽合肥 230601)
1 引言
现有的构造向量值有理插值函数方法都与连分式相联系[1-3],而用连分式计算是有条件的,就是假定在计算过程中每一步都是可行的,即不会出现分母为零,但在实际进行计算之前,却无法判定某一步会出现分母为零的情况.[1-3]即使出现分母为零的情况,也不能断言相应的插值函数不存在.[3]常用的基于连分式的计算是有条件限制,受较强约束的.为了避免这一缺点,本文给出一种约束较少,计算简单的构造向量值有理插值函数方法.
本文主要研究二元向量值有理插值函数的构造问题.首先给出二元向量值有理插值问题如下:
设x0 寻求向量值有理分式: (1.1) 使得 (1.2) 对于给定的插值条件,可以仿造构造多项式插值函数那样来构造插值公式.因此,本节引入多项式形式插值算子及待定的参数,用于构造二元向量值有理插值函数. 对于给定的x0 wi(x)=(x-x0)…(x-xi-1)(x-xi+1)…(x-xn), (2.1) 定义有理分式函数如下: (2.2) 其中, (2.3) 同理,对于给定的y0 wj(y)=(y-y0)…(y-yj-1)(y-yj+1)…(y-ym), (2.4) 定义有理分式函数如下: (2.5) 其中: (2.6) 构造插值算子: (2.7) 引入插值算子 (3.1) 显然 , i=0,1,…,n;j=0,1,…,m. (3.2) 这就是二元向量值有理插值公式。 (3.3) (3.4) (3.5) 故得: ι=0,1,…,n;k=0,1,…,m 故本节所构造的二元向量值有理插值公式满足插值条件. x0=-1,x1=0,y0=0,y1=1 解: 由式(3.1) 知插值算子 由式(2.2),(2.5)知 由公式(3.2)得 u=0,1;v=0,1i=0,1;j=0,1. 参考文献: [1]H E Salzer.Note on osculatory rational interpolation[J]. Math Comput,1962,16 (80): 486. [2]L Wuytack. On the osculatory rational interpolation problem[J].Math Comput, 1975,29(131):35. [3]程荣.构造向量值有理插值函数的方法[D].合肥:合肥工业大学,2007.9. [4]王仁宏, 梁学章. 多元函数逼近[M]. 北京:科学出版社,1988.37. [5]朱功勤, 顾传青, 向量连分式逼近与插值[J]. 计算数学,1992,14(4):427.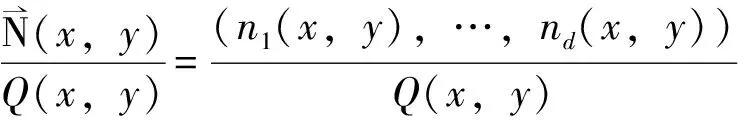
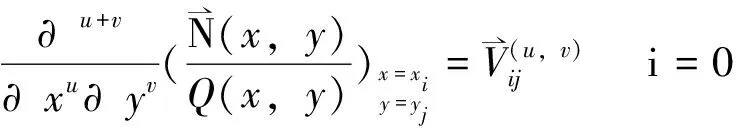
2插值算子的引入
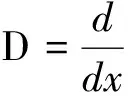
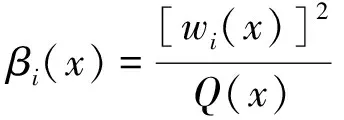
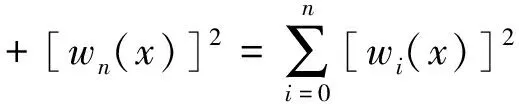
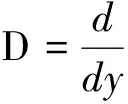
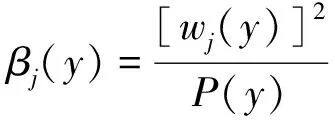
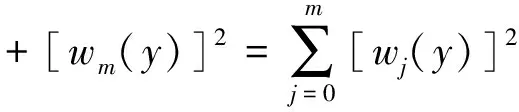
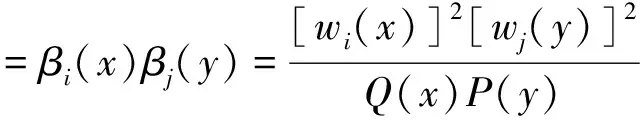
3向量值有理插值公式的构造
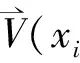
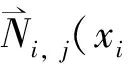
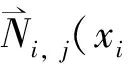
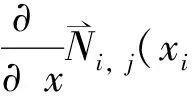
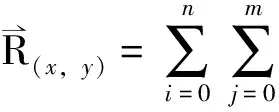
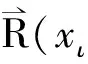
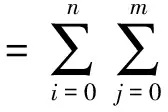
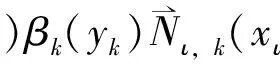
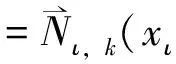
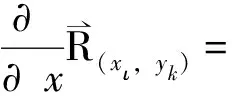
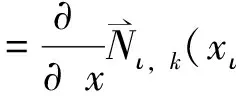
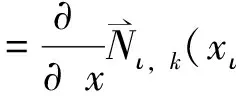
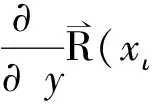
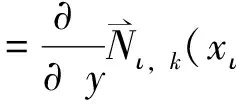
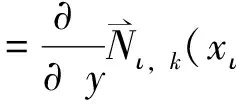
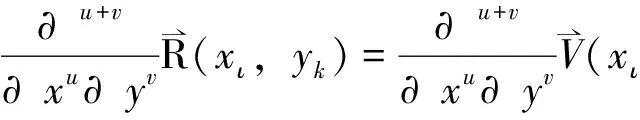
4举例