基于跳扩散过程的一类期权定价模型
2013-12-03张诚斌李辉来
袁 缘, 张诚斌, 李辉来
(吉林大学 数学学院, 长春 130012)
0 引 言
关于期权定价问题的研究目前已有很多结果. Brennan等[1]对期权定价做出了奠基性的工作, 其模型是: 假设在完美市场下, 设非杠杆企业价值为P, 杠杆企业价值为Q, 企业的债务利率为i, 所得红利为B, 企业的债务成本为C(P), 债务面值为A, 债务到期日为T, 非杠杆企业价值P满足如下随机常微分方程:
(1)
则在带红利支付时, 杠杆企业价值Q满足如下方程:
Mauer等[2]研究了代理成本和融资决策的期权问题; Sarkar[3]研究了税务对投资期权的影响; Leland[4]研究了波动率为常数时的债务价值问题, 并进一步讨论了企业资本问题[5]; Jiang等[6]讨论了期权理论问题; Harris等[7]研究了各行业的杠杆比例问题; Hackbarth等[8]讨论了再融资情况下的企业资本问题; Egami[9]研究了企业扩张期权时资本结构的一系列问题. 在上述工作的基础上, 本文进一步研究Brown运动和Poisson过程下期权定价的性质.
假设: 1) 企业经营良好, 不受企业财务的影响; 2) 企业原来决定的资本结构不会发生变化; 3) 市场趋于稳定, 企业发行的债券市场值不会发生变动.
1 主要结果
假设企业的资产价值S服从下列模型:
(3)
其中:μ(t)为企业的预期增长率;σ(t)为瞬时波动率; ex(t)-1表示在t时刻的跳跃高度. 用λ表示Possion过程N(t)t≥0的强度, 即在dt内出现一次跳的概率为λdt.
假设在t时刻企业的价值为F(S,t), 则由Brown运动的It公式, 有
(4)
其中〈·,·〉表示L2(0,T)上的内积,L2(0,T)由一些随机过程X(·)组成, 并且
由Brown运动和Possion过程的性质可知: 〈dW,dW〉=dt, 〈dW,dt〉=o(dt), 〈dN,dN〉=λt, 〈dN,dt〉=o(dt), 〈dN,dW〉=o(dt), 〈dt,dt〉=o(dt), 则〈dS,dS〉=S2(σ2+(ex-1)2λ)dt, 从而有
假设一个投资者进行如下投资组合: 先买入一份公司资产H(S,t), 再卖出一份公司债务F(S,t), 记所得价值为V(t), 则
V(t)=H(S,t)S-F(S,t).
(6)
设ΔV,ΔS,ΔF分别是Δt时间内V,S,F的变化, 则
(7)
由于投资者在Δt内获得一定价值的同时也会失去一些利息收入AΔt, 因此在Δt内的收益为ΔV(t)-AΔt. 由于ΔV(t)-AΔt是无风险的, 所以由无套利原理, 有ΔV(t)-AΔt=r(t)VΔt.
设红利率为g(t), 则支付红利为g(t)H(S,t)Sdt, 故
ΔV(t)-AΔt=r(t)VΔt-g(t)H(S,t)Sdt,
从而有
(8)
下面求解方程, 设u=Feβ(t),y=Seα(t), 则
将式(9)代入式(8), 并消去e-β(t), 可得
(10)
设α(t)和β(t)是如下常微分方程初值问题的解:
易得

则问题(8)等价于
(11)
令y=eh, 则ymDmu=D0(D0-1)…(D0-m+1), 其中D0=d/dx, 则式(11)变为
(12)
进一步, 由于τ=T-t, 则式(12)可化为
(13)
考虑
(14)
引入式(14)的惩罚问题:
(15)
其中:K是敲定价;
(16)
定义1如果函数βε(x)满足如下条件:
(x)≤0;
(17)
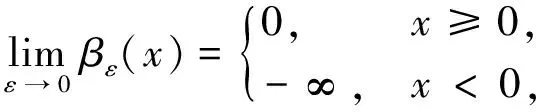
(18)
则称βε(x)为R上的惩罚函数.
引理1[6]设uε(x,t)是惩罚问题(15)的解, 则当ε→0时, 在DT={(x,t)|a 引理2[7]对于期权定价, 若t1≥t2, 则u(s,t2)≥u(s,t1). 定理1在期权定价中, 若T1≥T2, 则当0≤t≤T2时,u(S,t;T1)≥u(S,t;T2). 证明: 设 H(x,τ)=uε(x,τ,T1)-uε(x,τ,T2) (τ=T2-t), (19) 其中uε(x,τ,Ti)=ui(x,τ), 且ui(x,τ)满足式(15). 考虑区域x∈R, 0≤τ≤T2, 把ui(x,τ)(i=1,2)代入式(15)后相减并运用微分中值定理, 可知H(x,τ)满足: (20) 其中 ζ(x)=uε(x,0,T1)-uε(x,0,T2)=uε(x,0,T1)-Aε(K-ex). (21) 因为在x∈R, 0≤τ≤T2中,uε(x,τ,T2)满足式(15), 故uε(x,0,T2)=Aε(K-ex). 同理在x∈R, 0≤τ1≤T1中, 可得uε(x,τ1,T1)满足式(15), 故uε(x,0,T1)=Aε(K-ex). 由t=T-τ, 得 uε(x,T1,T1)=Aε(K-ex), 再由引理2可得 ζ(x)=uε(x,T2,T1)-Aε(K-ex)=uε(x,T2,T1)-uε(x,T1,T1)≥0. 应用比较原理, 知H(x,τ)≥0, 即uε(x,τ,T1)≥uε(x,τ,T2). 令ε→0, 得u(S,t;T1)≥u(S,t;T2). 定理1表明, 在到期日前的任意一个时刻, 到期时间越长, 看跌期权价格越大. 定理2在期权定价中, 若σ1≥σ2, 则u(S,t;σ1)≥u(S,t;σ2). 证明: 设 H(S,τ)=u1(x,τ)-u2(x,τ), (22) 其中ui(x,τ)=uε(x,τ,σi), 则H(x,τ)满足方程: 及初始条件 H(x,0)=u1(x,0)-u2(x,0)=0. (24) 由引理3可知式(23)右端非负, 从而利用比较原理, 得H(x,τ)≥0, 即uε(x,τ,σ1)≥uε(x,τ,σ2). 令ε→0, 得u(S,t;σ1)≥u(S,t;σ2). 定理2表明, 波动率越大, 看跌期权价格越大. [1] Brennan M J, Schwartz E S. Optimal Financial Policy and Firm Valuation [J]. The Journal of Finance, 1984, 39(3): 593-607. [2] Mauer D C, Sarkar S. Real Options, Agency Conflicts, and Optimal Capital Stucture [J]. Journal of Banking and Finance, 2005, 29(6): 1405-1428. [3] Sarkar S. Can Tax Convexity Be Ignored in Corporate Financing Decisions [J]. Journal of Banking and Finance, 2008, 32(7): 1310-1321. [4] Leland H E. Corporate Debt Value, Bond Covenants and Optimal Capital Structure [J]. The Journal of Finance, 1994, 49(4): 1213-1252. [5] Leland H E. Agency Costs Risk Management and Capital Structure [J]. The Journal of Finance, 1998, 53: 1213-1243. [6] JIANG Xian-feng, SHI Yong-dong, Jiang G. Real Options under Jump Diffusion Process: What Type of Jumps [J/OL]. 2008-08. http://ssrn.com/abtract=1361576. [7] Harris M, Raviv A. The Theory of Capital Stucture [J]. The Journal of Finance, 1991, 46(1): 297-355. [8] Hackbarth D, Mauer D C. Optimal Priority Stucture, Capital Structure, and Investment [J/OL]. 2011-12-13. http://rfs.oxfordjournals.org/content/early/2011/12/12/rfs.hhr129. [9] Egami M. A Framework for the Study of Expansion Options, Loan Commitments and Agency Costs [J]. Journal of Corporate Finance, 2009, 15(3): 345-357.
2 期权的性质
