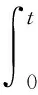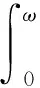时标线性微分方程组的Massera准则

张 宇,索忠林,任 彪

(1.空军航空大学 基础部,长春 130022；2.山西建筑职业技术学院,太原 030006)

在微分方程理论中,周期解的存在性研究已取得了丰富成果.Massera[1]证明了常微分方程x′=A(t)x+f(t)存在ω-周期解的充要条件是方程有一个在1上有界的解;文献[2-3]对其进行了不同形式的推广;Hilger[4]初步建立了时标上动态方程的基本理论.目前对时标理论的研究已引起人们广泛关注[5-7].本文讨论时标线性微分方程组的Massera准则.

参考文献[8],时标理论的相关定义及性质如下.

定义1时间标度(time scales)简称时标,即实数集的任意一个非空闭子集,用 T表示.

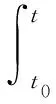
定义2令 T是一个时标,对t∈T,前向跳跃算子σ: T→T,后向跳跃算子ρ: T→T和步差函数μ: T→[0,∞)分别由σ(t)∶=inf{s∈T:s>t},ρ(t)∶=sup{s∈T:s

下面考虑定义在时标上的函数f,可以定义它在点t∈Tk处的Δ导数.

定义3设函数f: T→n,t∈Tk,对任意的ε>0,存在t的邻域U,使得对任意的s∈U,有|[f(σ(t))-f(s)]-fΔ(t)[σ(t)-s]|≤ε|σ(t)-s|成立,则称f在t处Δ可导.

注11) 令 T=,则σ(t)=t,μ(t)=0,fΔ=f′是通常意义下的导数;2) 令 T=,则σ(t)=t+1,μ(t)=1,fΔ=Δf是通常意义下的前移差分算子.

定义4设f(t)在 T上有定义,如果存在一个不为零的常数ω,使得当t∈T时,f(t+ω)=f(ω)都成立,则称函数f(t)为ω-周期函数.

下面给出本文的主要结果.考虑一阶线性时标微分方程组

yΔ=A(t)y+f(t),y(t0)=y0,

(1)

其中:A(t)为 T上的n×n矩阵值函数;A: T→n×n和f: T→n是右连续的;t0∈T;y0∈n.则由常数变易公式,方程(1)有唯一解y: T→n,且其解为

(2)

其中ΦA(t,t0)是初值问题yΔ=A(t)y,y(t0)=y0的基本解矩阵.显然有下列性质:

Φ0(t,s)=I,ΦA(t,t)=I;

(3)

ΦA(t,s)ΦA(s,r)=ΦA(t,r).

(4)

定理1若A(t)和f(t)在 T上有定义,并且是ω-周期函数,则方程组(1)存在ω-周期解的充要条件是方程(1)有一个在 T上的有界解.

证明：必要性显然,只需证明充分性.

设y=y0(t)是方程(1)于 T上有界的解.由A(t)和f(t)在 T上是ω-周期函数,对任意正整数k,y0(t+(k-1)ω)是满足初始条件y0=y0((k-1)ω)的解,则由式(2)及式(4)有

从而

y0(kω)=ΦA(ω,0)y0((k-1)ω)+v,k=1,2,3,…,

(5)

联合式(5),(6)可得

uTy0(kω)=uTy0(0)+kuTv,k=1,2,3,….

(8)

又由于式(7)成立,而y0(t)是有界的,故当k充分大时,式(8)不可能成立.从而方程(1)有ω-周期解.

[1] Massera J L.The Existence of Periodic Solutions of Systems of Differential Equation [J].Duke Math J,1950,17(4): 457-475.

[2] LI Yong,CONG Fu-zhong,LIN Zheng-hua,et al.Periodic Solutions for Evolution Equations [J].Nonlinear Anal: Theory,Methods &Applications,1999,36(3): 275-293.

[3] XIA Zhi-nan,FAN Meng.A Massera Type Criterion for Almost Automorphy of Nonautonomous Boundary Differential Equations [J].Electronic Journal of Qualitative Theory of Differential Equations,2011,73: 1-13.

[4] Hilger S E.Maβkettenkalkülmit Anwendung Auf Zentrumsmannig-Faltigkeiten [D].Würzburg,Germany: Univerditt Würzburg,1988.

[5] LIU Xi-lan,LI Wan-tong.Periodic Solutions for Dynamic Equations on Time Scales [J].Nonlinear Analysis：Theory,Methods &Applications,2007,67(5): 1457-1463.

[6] Federson M,Mesquita J G,Slavik A.Measure Functional Differential Equations and Functional Dynamic Equations on Time Scales [J].Journal Differential Equations,2012,252(6): 3816-3847.

[7] Zafer A.The Stability of Linear Periodic Hamiltonian Systems on Time Scales [J].Applied Mathematics Letters,2013,26(3): 330-336.

[8] Bohner M,Peterson A.Dynamic Equations on Time Scales.An Introduction with Applications [M].Boston: Birkhäuser,2001.