经济结构变迁下的城市化发展:实证与启示
2013-12-03杨小勇
杨小勇, 吕 健
(1. 同济大学 马克思主义学院, 上海 200092; 2. 上海金融学院 经济系, 上海 201209)
一、引言及文献回顾
诺贝尔经济学奖获得者约瑟夫·斯蒂格利茨(Joseph E.Stiglitz)曾说过,21世纪将会有两件大事影响人类的进程,一是新技术革命,二是中国的城市化。城市化是由以农业为主的传统乡村社会向以工业和服务业为主的现代城市社会逐渐转变的历史过程,也是衡量一个国家和地区经济、社会、文化和科技水平的重要标志。作为世界上人口最多的国家,中国的城市化进程必然将对整个人类的进程产生重要影响。中国的城市化率在1978年只有17.9%,到了2000年翻了一番,达到36.2%,而在2009年,这一比率提高至46.6%。改革开放以来,中国的经济体制由计划经济逐步转向市场经济,经济结构的转变倍受关注。1978年,第一、二、三产业在国内生产总值中的比重分别为28.2%、47.9%和23.9%,而到了2011年,第一产业比重已降至10.1%,第三产业比重上升至43.1%,经济结构出现了显著的变化。但是,由于中国长期以来处于制造业大国的地位,第二产业比重虽有下降的趋势,但并不明显,2011年第二产业比重仍占46.8%。根据城市经济学理论,城市化是在空间体系下的一种经济转化过程,非农人口和非农产业在城市集中是集聚效应和辐射效应产生的结果。也就是说,经济结构的变化可以有力地推动城市化的发展,而反过来,城市化水平的提高也会为经济结构的转变创造条件。
早在17世纪中叶,威廉·配第就指出,非农产业的收益高于农业,会驱使劳动力这种生产要素向非农产业转移。亚当·斯密也认为,生产要素,尤其是资本,首先是投向农业,之后便会转向制造业、国际贸易等非农产业。而这种经济结构的转变,恰好有利于城市化的发展。20世纪60年代之后,西方学界对于城市化与经济结构之间关系的研究日渐增多。Kuznets(1966)在考察经济结构变动所产生的结果时,发现经济结构变动对城市化的影响是由产业的不同属性引起的。*S. Kuznets, Modern Economic Growth: Rate, Structure, and Speed, New Haven: Yale University Press, 1966.Chenery(1975)对经济发展各个时期的经济结构变动和城市化发展的轨迹进行了实证分析,提出了经济结构变动与城市化相互关联的问题。*H. B. Chenery, and M. Syrquin, Patterns of Development, 1950-1970, London: Oxford University Press, 1975.Lucas(1988)认为,由于经济结构的转变,使得人力资本向城市集聚,并成为推动城市化发展的动力。*R. Lucas, “On the Mechanics of Economic Development”, Journal of Monetary Economics, 1988,(22): 3-42.Davis和Henderson(2003)也认为,经济结构的变化,使得生产要素集聚和人口集聚产生了规模效益,从而促进了城市化的发展。*J. C. Davis, and J. V. Henderson, “Evidence on the Political Economy of the Urbanization Process”, Journal of Urban Economics, 2003,(53): 98-125.类似的研究还有Murata(2002)*Y, Murata. Rural-Urban Interdependence And Industrialization, Journal of Development Economics, 2002,68(1): 1-34.、Kondo(2004),*H. Kondo, “Multiple Growth and Urbanization Patterns in an Endogenous Growth Model with Spatial Agglomeration”, Journal of Development Economics, 2004,(75): 167-199.等等。
国内学者关于城市化与经济结构之间关系的研究同样较为广泛和深入。此类研究主要分为两种类型:一是规范分析,主要研究城市化与经济结构(特别是产业结构)之间的相互关系。大多数学者认为城市化与经济结构之间具有密切的关系,如钟水映、李晶(2002)*钟水映、李晶:《经济结构、城市结构与中国城市化发展》,《人口研究》,2002年第5期,第63-70页。,欧阳峣、生延超(2006)*欧阳峣、生延超:《城市化水平与产业结构调整的内在互动机制》,《广州大学学报(社会科学版)》2006年第11期,第47-51页。等;也有部分学者认为中国的经济结构变化对城市化发展没有明显作用,如郭克莎(2002)*郭克莎:《工业化与城市化关系的经济学分析》,《中国社会科学》,2002年第2期,第44-55页。、蒋满元(2005)*蒋满元:《城市化与经济结构演变互动机制的逻辑模型及分析》,《现代经济探讨》,2005年第12期,第34-37页。等。二是实证分析,主要通过实证的方法,从三次产业的角度分析经济结构变化对城市化发展的影响。如张雷、朱守先(2008)*张雷、朱守先:《现代城市化的产业结构演进初探——中外发展演进对比》,《地理研究》,2008年第4期,第863-872页。,刘艳军、李诚固、王颖(2010)*刘艳军、李诚固、王颖:《中国产业结构演变城市化响应强度的省际差异》,《地理研究》,2010年第7期,第1291-1304页。,等等。此外,值得关注的是,蒋伟(2009)*蒋伟:《中国省域城市化水平影响因素的空间计量分析》,《经济地理》,2009年第4期,第613-617页。、吕健(2011)*吕健:《中国城市化水平的空间效应与区域收敛分析:1978-2009年》,《经济管理》,2011年第9期,第32-44页。等学者结合地理空间因素,运用空间计量经济学方法分析了中国城市化的空间集聚效应,以及与经济增长之间的关系,获得了有益的结论。
与目前国内已有的研究不同的是:第一,本文并不是沿用传统的计量分析方法,而是把地理空间因素纳入到分析框架之中,利用空间计量模型,研究经济结构变化对城市化发展的影响作用。第二,根据中国城市化水平和第二、三产业水平的空间相关性的变动规律,把改革开放以来的34年观测期划分为4个时段,能够更好地反映出在空间相关性存在的情况下,经济结构变迁对城市化发展的影响轨迹。
二、研究方法和样本数据
1. 研究方法
随着空间异质理论的提出,近年来,空间计量分析技术已经在诸多领域得到广泛地应用。本文将采用空间自相关和空间常系数回归模型这两种最为常用的空间分析方法。
(1) 空间自相关
空间自相关包括全局空间自相关和局部空间自相关。全局空间自相关是从区域空间的整体上刻画区域经济活动分布的集聚情况,常用的指数是Moran’sI。Moran’sI的取值范围一般为[-1,1],大于0表示空间正相关,小于0表示空间负相关,等于0表示空间不相关。一般认为,如果Moran’sI的正态统计量的Z值大于正态分布函数在5%水平下的临界值1.65,表明区域经济活动在空间分布上具有显著的正相关性,这也意味着相邻区域的类似特征值出现了集聚效应(LeSage,1999)。*J. P. LeSage, The Theory and Practice of Spatial Econometrics, Department of Economics, University of Toledo, 1999.局部空间自相关描述的是不同地理位置的区域空间关联模式,即某一区域周边具有显著相似值区域的集聚程度(Anselin,1995),*L. Anselin, “Local Indicators of Spatial Association-LISA”, Geographical Analysis, 1995,27(2): 93-115.常用的指标为局部Moran’sIi。Moran’sIi>0表示该区域与邻近区域的特征值相似;Moran’sIi<0表示该区域与邻近区域的特征值不相似。因此,局域空间自相关可以揭示具体区域的辐射效应。
此外,Moran’sI散点图能够进一步区分某个地区与其相邻地区之间的空间联系形式。Moran’sI散点图具有4个象限,分别对应于相邻地区之间4种类型的空间联系形式(徐建华,2006)。*徐建华:《计量地理学》,北京:高等教育出版社,2006年,第120-151页。第Ⅰ、Ⅲ象限代表观测值之间存在正的空间自相关(高—高、低—低集聚),而第Ⅱ、Ⅳ象限代表观测值之间存在负的空间自相关(低—高、高—低集聚)。
(2) 空间常系数回归模型
通常,空间计量模型主要有两类:当变量之间的空间依赖性对模型显得非常关键而导致了空间相关时,采用空间滞后模型(SLM);当模型的误差项在空间上相关时,采用空间误差模型(SEM)(Anselin 等,2004)。*L. Anselin, J. G. M. Raymond, and R. J. Florax, Advances in Spatial Econometrics: Methodology, Tools and Applications, Berlin: Springer-Verlag, 2004: 1-3.
空间滞后模型的表达式为:
y=ρWy+βX+ε
其中,y为因变量,X为n×k的外生解释变量矩阵,ρ为空间回归系数,反映了样本观测值中的空间依赖作用,即相邻地区的观测值Wy对本地区观测值y的影响方向和程度,W为n×n阶空间权重矩阵,Wy为空间滞后因变量,ε为随机误差项向量。
空间误差模型的表达式为:
y=βX+ε
ε=λWε+μ
其中,ε为随机误差向量,λ为n×1阶的截面因变量向量的空间误差系数,μ为正态分布的随机误差向量。模型中参数β反映了自变量X对因变量y的影响,参数λ衡量了样本观测值中的空间依赖作用。存在于扰动误差项之中的空间依赖作用,可以度量邻近地区关于因变量的误差冲击对本地区观测值的影响程度。
(3) 模型的判别与估计
判断某一经济现象是否存在空间自相关,以及空间滞后模型和空间误差模型哪个更恰当,一般可以通过Moran’sI检验、两个Lagrange Multiplier形式(LMLAG和LMERR)及其稳健性形式(Robust-LMLAG和Robust-LMERR)来实现。Anselin和Florax(1995)提出了如下判别标准:如果在空间自相关的检验中发现LMLAG较之LMER在统计上更加显著,且Robust-LMLAG显著而Robust-LMERR不显著,可以认为空间滞后模型较为合适;反之,则须选择空间误差模型。*L. Anselin, and R. Florx, New Directions in Spatial Econometrics, Berlin: Springer-Verlag, 1995: 21-71.
在模型估计中,由于以上两种空间模型自变量的内生性,如果仍采用最小二乘法(OLS),系数估计值会有偏或者无效,需要通过工具变量法(IV)、极大似然法(ML)或者广义最小二乘估计(GLS)、广义矩估计(GMM)等其他方法来进行。本文将根据Anselin(1988)的建议*L. Anselin, Spatial Econometrics: Methods and Models, Dordrecht: Kluwer Academic Publishers, 1988: 1-10.,采用极大似然法估计空间滞后模型和空间误差模型中的参数。
2. 样本数据
本文采用的空间样本是除了中国的台湾、香港、澳门等3个地区之外的内地31个省、自治区、直辖市(下文简称“省域”),主要选取1978-2011年的以下数据:
(1) 城市化水平。该指标主要反映的是城市人口规模。在现有文献中,有用城市人口占城市和农村总人口比重来表示的,也有用城市就业人口占整体就业人口的比重表示的,还有两者兼顾的。这里,我们采用较为常用的表示方法,即城镇人口占总人口的比重。
(2) 第二产业水平。该指标采用第二产业产值占地区生产总值的比重。这里的第二产业主要包括工业和建筑业。
(3) 第三产业水平。该指标采用第三产业产值占地区生产总值的比重。这里的第三产业主要包括交通运输和仓储业、批发和零售业、住宿和餐饮业、金融和房地产业、邮政业等。
以上使用的数据均来自《新中国60年统计资料汇编》和《中国统计年鉴》相关各期;在所有回归模型的估计中,为了避免量纲及异方差的影响,我们采用自然对数对原始数据进行处理;研究中所使用的地理信息与地图,均由地理信息系统(GIS)软件生成。
三、空间自相关分析
在进行空间分析之前,首先要对空间权重矩阵进行设定。目前,常用的空间权重矩阵有9种,每种空间权重矩阵得到的Moran’sI数值都是不同的。我们通过对rook一阶邻接关系和二阶邻接关系(即邻居的邻居)进行实证,发现选择rook一阶空间权重矩阵较为理想。原因是选择rook一阶之后,随着阶数的升高,所得到的各个年份的省域Moran’sI数值逐阶下降,说明经济活动的空间相关性随着空间距离的增大而减小,符合地理学第一定理(Tobler,1970)。*W. A. Tobler, “Computer Movie Simulating Urban Growth in the Detroit Region”, Economic Geography, 1970,46(2): 234-240.
1. 全局空间自相关
通过对城市化的全局空间自相关进行分析,我们发现,在1978-2011年,中国31个省域城市化的全局Moran’sI数值都大于零,标准化检验的Z统计量均为正,且都通过了显著性检验*城市化的全局Moran’s I,除少数年份仅通过10%显著性水平检验之外,其他年份均通过了5%的显著性水平检验。,可以拒绝不存在自相关的原假设。由此可知,中国各个省域的城市化存在着全局空间自相关,也就是说,城市化水平相似的区域一直存在着空间集聚效应。此外,我们也计算了第二、三产业的全局Moran’sI,在图1中一并绘出,以便比较。
根据各个省域城市化的全局Moran’s I的变化特征(如图1所示),本文在接下来的研究中,把1978-2011年这一考察时期划分为4个时段,即1978-1986、1987-1994、1995-2002、2003-2011。而在数据处理上,我们采用各项指标在时段内的平均值来刻画该时段的相应特征。
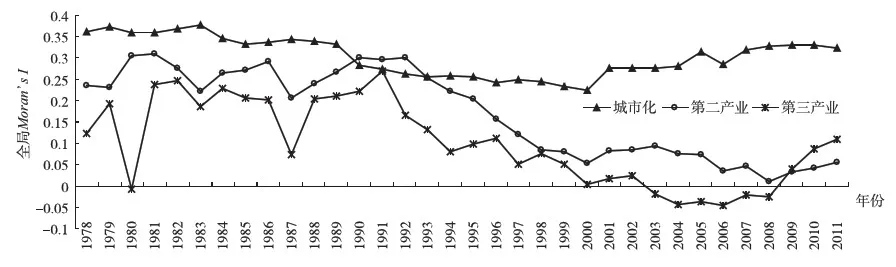
图1 1978-2011年各省域城市化和第二、三产业发展的全局Moran’s I
通过对上述4个时段全局Moran’sI的散点图进行分析,可以发现:从整体趋势来看,处于“高—高”集聚和“低—低”集聚的省域较多,处于“低—高”集聚和“高—低”集聚的省域较少,处于第Ⅰ、Ⅲ象限的省域如表1所示。通过具体的分析,我们可以发现,第一,城市化高值集聚的省域在1978年主要集中于京津和东北地区,随后扩大到长三角地区。第二,长期以来,中国大部分省域(包括一些较发达的省域)处于低值集聚区域。第三,作为珠三角中心的广东,在1986年之后脱离了低值集聚区域,但尚未形成高值集聚。这种集聚效应形成的原因主要与国家的经济社会发展战略和省域自身条件差异有关。长期的计划经济,使得京津和东北地区工业化水平普遍较高,大量人口集聚在城市,从而形成较高的城市化水平。中国市场经济的建立,以及东部率先发展战略的实施,有力地推动了东部沿海特别是长三角地区的城市化发展。随着改革开放的深入和区域发展战略的实施,各个省域自身条件的差异进一步地体现在经济社会发展水平上,使得东部沿海省域与其他省域在城市化发展水平上差距更加明显。此外,一些经济比较发达的省域(如山东)由于长期处于农业大省的地位,也使得其城市化的发展受到了制约。在这一系列因素的综合作用之下,中国的省域城市化发展呈现出了明显的“马太效应”。
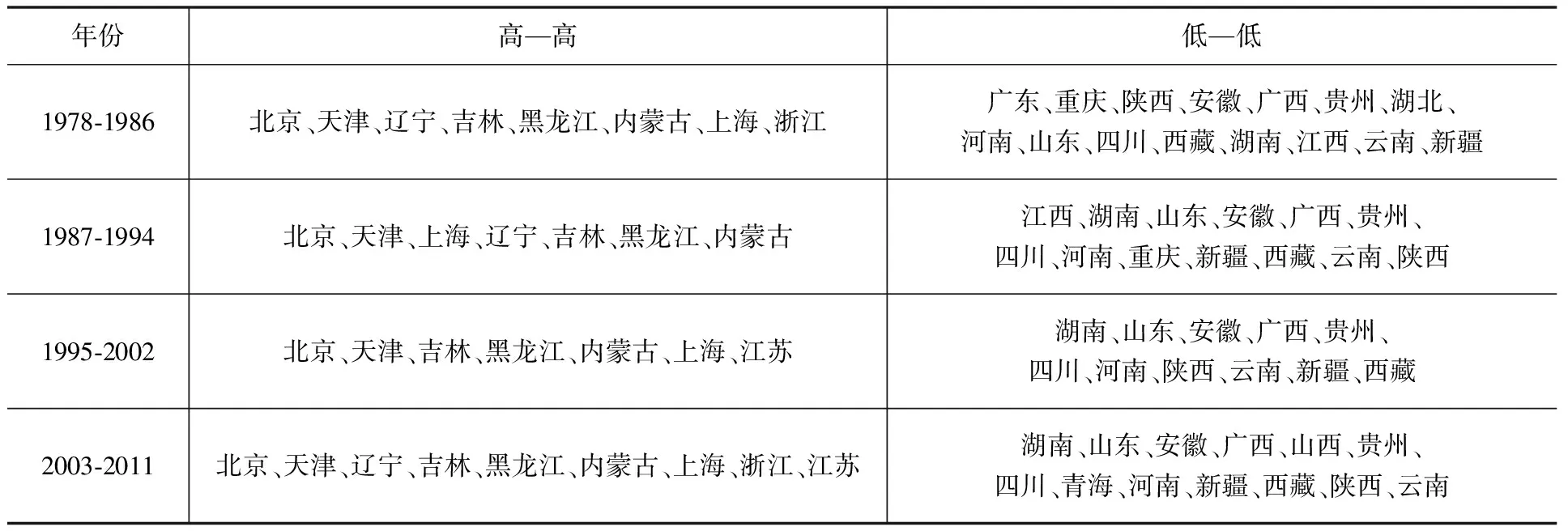
表1 1978-2011年全局Moran’s I散点图对应省域
2. 局部空间自相关
以上我们通过计算全局Moran’sI,发现中国省域城市化存在全局空间自相关,但是该统计量不能显示局部地区的空间自相关,即无法观察到具体省域对周边省域的辐射效应,因此,我们需要使用局部Moran’sI和局部空间效应地图来做进一步分析。
在局部Moran’sI的散点图中,处于第Ⅰ、Ⅲ象限的“高—高”和“低—低”类型省域表现为局部正相关,这表明高(低)观测值省域对包围它的高(低)观测值的省域存在着辐射作用。处于第Ⅱ、Ⅳ象限的“低—高”和“高—低”类型省域表现为局部负相关,表明不具有辐射效应。为了直观起见,我们把处于4个象限中的省份用不同的颜色在地图上标记出来,如图2所示。
通过图2可以发现:1978-1986年,在城市化发展上,产生高值集聚的省域是天津和吉林,低值集聚的省域为重庆、云南、贵州。1987-1994年,高值集聚的省域出现了略微的变化,但仍集中在京津和东北地区(北京、吉林);低值集聚的省域是山东、重庆、云南和贵州。1995-2002年,由于空间自相关系数在这一时段下降至最低点,未出现呈现高值集聚的省域,而低值集聚的省域依然是山东、云南和贵州。2003-2011年,高值集聚的省域为北京、天津和上海,低值集聚的省域由之前的云南、贵州扩大到四川和西藏。从整体上看,在1978-2011年的4个时段上,表现为出高(低)值集聚且通过5%水平显著性检验的省域基本上是东部(西部)省域。从动态演进过程看,高值集聚日益明显,涉及的省域也有所增加,即从早期的京津和东北地区演变到现今京津沪地区;低值集聚的省域从之前的云贵渝地区发展到现在的云贵川藏地区。
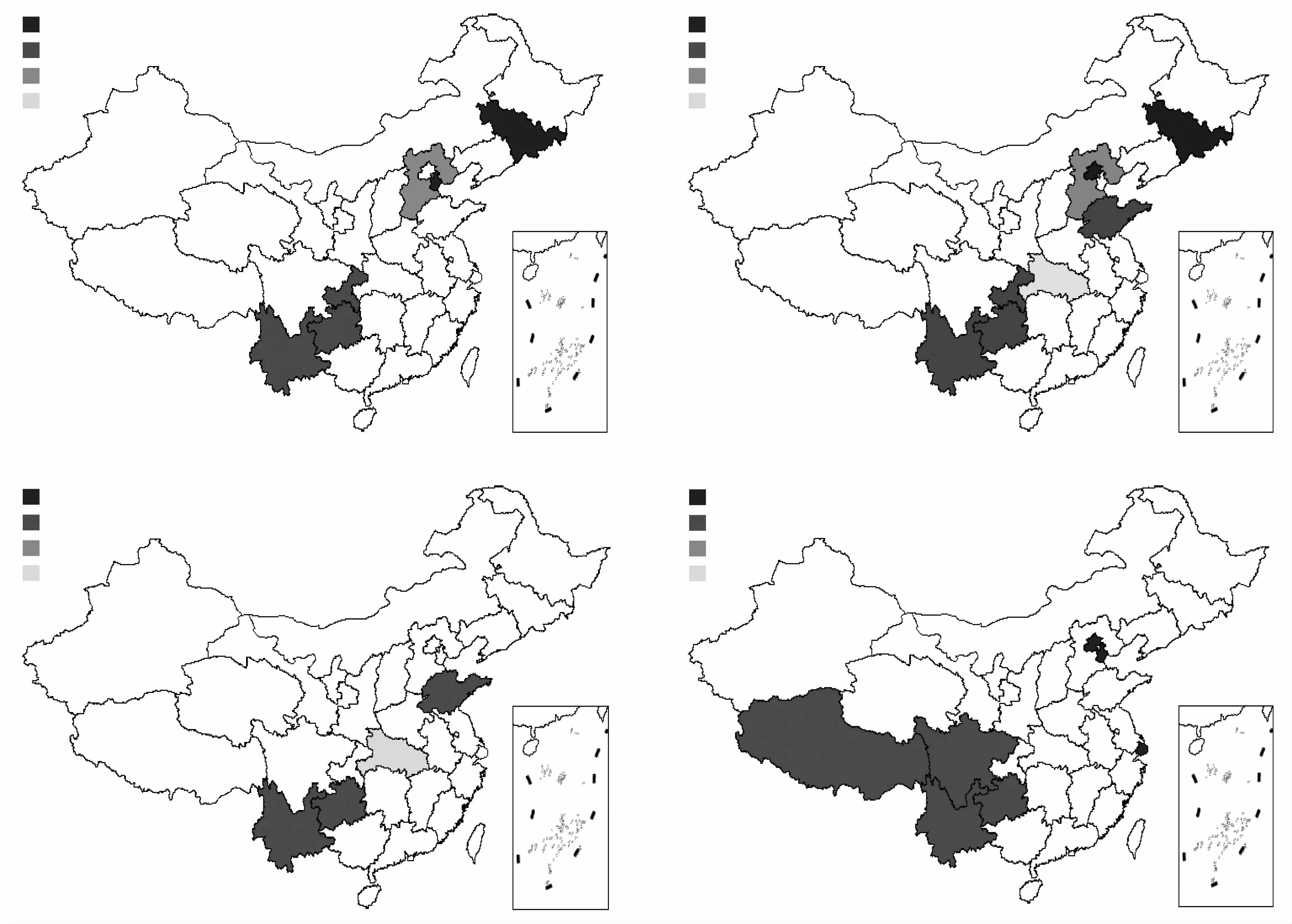
图2 2001-2011年中国各省域城市化的局部空间效应
四、空间模型估计
空间自相关分析虽然从全局和局部两个方面揭示了城市化的集聚和辐射效应,但是并不能揭示城市化与经济结构之间的关系。因此,有必要建立空间计量模型进一步分析,探寻省域城市化和经济结构的深层关系。接下来,我们以城市化水平(URBAN)为被解释变量,以地区生产总值中的第二产业比重(SI)和第三产业比重(TI)作为解释变量,构建回归模型。为了考察存在空间因素与否所产生的不同结果,我们首先进行普通回归模型估计。
1. 普通回归模型
基于双对数模型,我们可以建立如下的普通回归模型:
lnURBAN=c+β1lnSI+β2lnTI+ε
其中,c为常数项,β为回归系数,ε为随机误差项。该模型的目的是检验省域的城市化水平与第二、三产业水平之间的相互关系和决定因素;进一步地,通过Moran’sI检验、两个Lagrange乘数及其稳健性来判断空间回归模型SLM和SEM的形式。
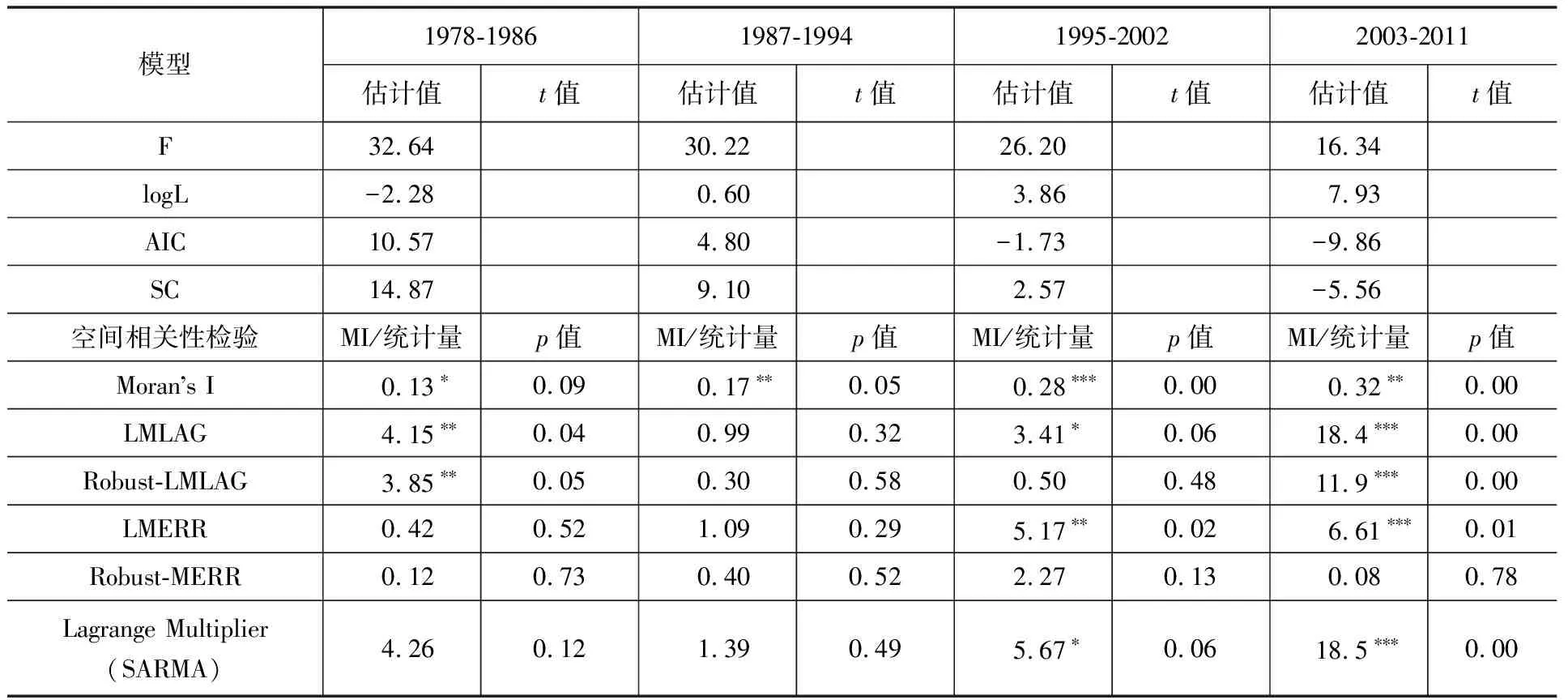
我们分别对4个时段的样本数据进行OLS回归*每时段各个变量所采用的数据均为该时段内年份的平均值。,结果如表2所示。
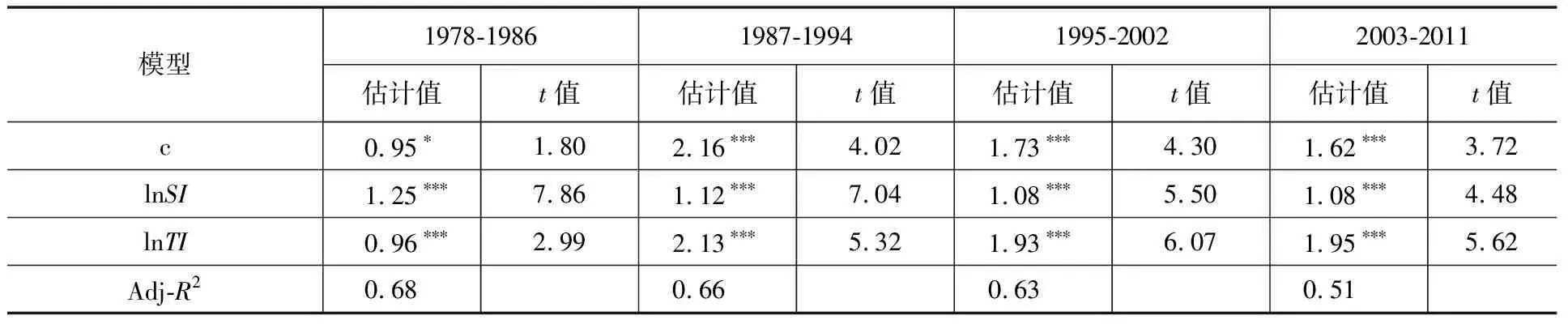
表2 普通回归模型估计结果(1978-2011年)
续表2
注:***、**、*分别表示通过1%、5%、10%水平下的显著性检验。
由回归结果可知,OSL估计的31个省域的城市化在4个时段的模型中,拟合优度分别为0.68、0.66、0.63和0.51。F值均较高,说明模型整体通过了1%显著性水平的检验。但是,Moran’sI检验显示出31个省域的城市化水平之间具有明显的空间自相关(特别是后3个时段,显著性水平均小于5%),存在空间集聚现象。这说明忽视空间自相关而直接采用OLS法建立模型进行估计分析存在一定的问题,譬如遗漏了重要的变量,或是未考虑截面单元(省域)之间的空间相关性。
2. 空间回归模型
为了进一步验证空间自相关的存在,我们根据两个Lagrange乘数滞后和误差及其稳健性(Robust)的检验结果选择SLM或SEM模型进行空间计量分析。
城市化的SLM模型表达式如下:
lnURBAN=c+ρWlnURBAN+β1lnSI
+β2lnTI+ε
城市化的SEM模型表达式如下:
lnURBAN=c+λεW+β1lnST+β2lnTI+μ
其中,W为空间权重矩阵,ρ为空间回归系数,λ为空间误差系数,ε为随机误差项,μ为正态分布的随机误差项。
表2中Lagrange乘数及其稳健性检验表明,除了1987-1994年的模型中两个Lagrange乘数及其稳健性没有通过显著性水平检验之外,其他3个时段模型的Lagrange乘数及其稳健性均有通过显著性水平检验的情况。根据上文所述的空间回归模型的判别标准,我们认为:1978-1986年和2003-2011年的模型应该选择空间滞后模型(SLM);1995-2002年的模型应该选择空间误差模型(SEM);而1987-1994年的模型,虽然其两个Lagrange乘数及其稳健性均没有通过10%水平的显著性检验,但是,通过比较两种模型的logL、AIC、SC和LR等指标,可以判断空间误差模型相对更好一些,当然,这种判断不是特别严格。4个时段的空间计量模型的估计结果如表3所示。
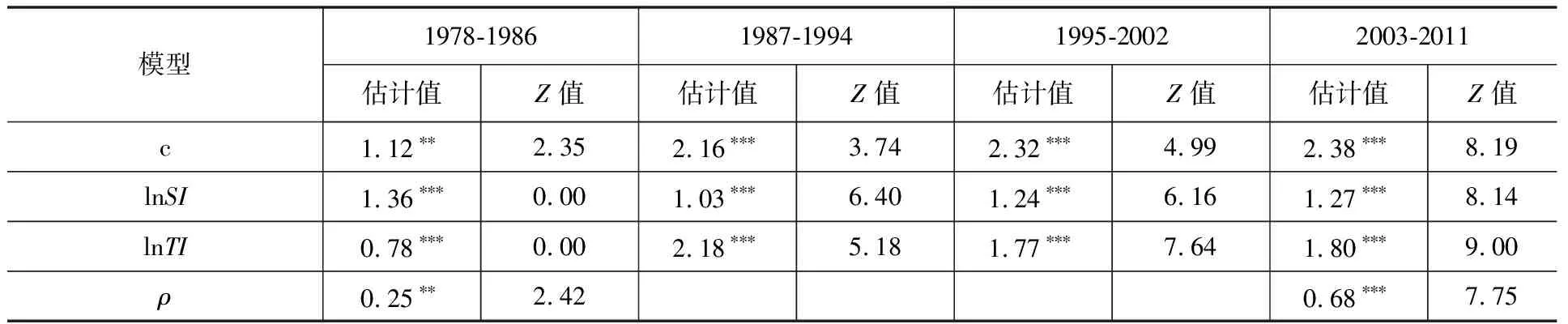
表3 空间回归模型估计结果(1978-2011年)
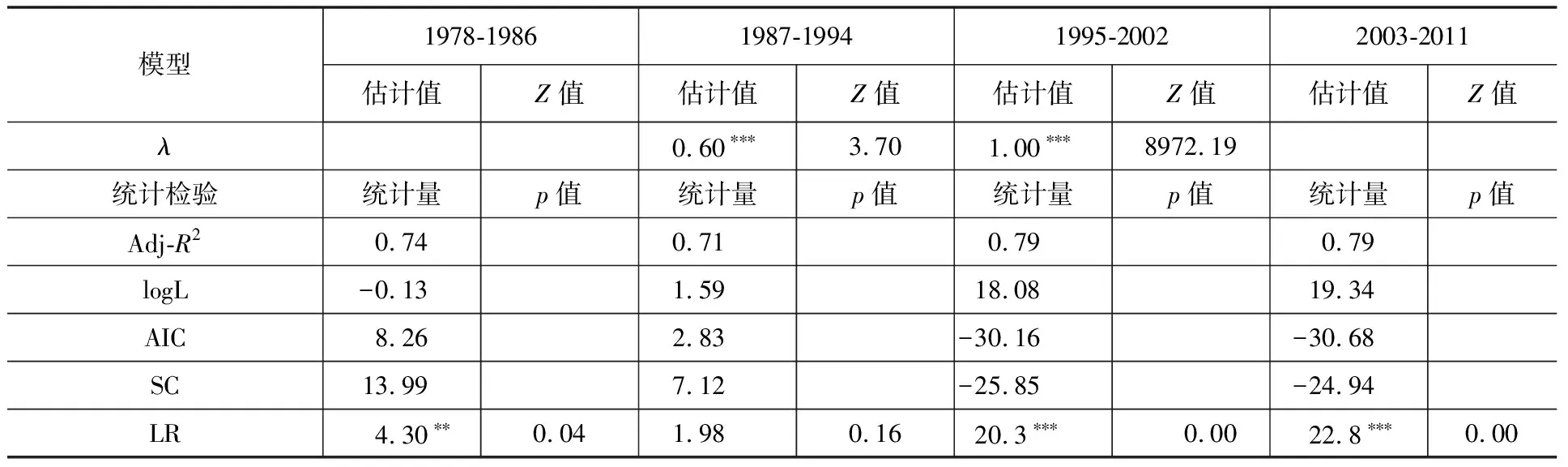
续表3
注:***、**、*分别表示通过1%、5%、10%水平下的显著性检验。
比较表2和表3中的估计结果发现,4个空间回归模型的拟合优度检验值均明显高于普通回归模型,当然,由于采用极大似然法估计参数,基于残差平方和分解的拟合优度检验意义不是很大。进而,我们比较对数似然函数值LogL、AIC和SC值之后发现,4个时段的空间回归模型的LogL值均高于相应的普通回归模型,AIC和AC值均小于相应的普通回归模型。由此可见,OLS回归法由于遗漏了空间误差自相关,使得普通回归模型不够恰当;同时,这也说明,省域之间的城市化不可能没有关系。
从表3中的4个时段的空间回归模型估计结果还可以看出,在考虑了空间自相关之后,出现了如下的变化:
首先,第二产业水平对城市化的影响程度(弹性)从第1时段的1.36下降至第4时段的1.27,且在第2时段降幅最大,除此时段外,其他三个空间回归模型结果与相应的普通回归模型相比,都有所上升。这说明若未考虑空间因素,则会低估第二产业水平对城市化的影响。
其次,第三产业水平对城市化的影响程度(弹性)从第1时段的0.78上升至第4时段的1.80,且在第2时段增幅最大,除此时段外,其他三个空间回归模型结果与相应的普通回归模型相比,都有所下降。这说明若未考虑空间因素,则会高估第三产业水平对城市化的贡献。
由以上变化不难得知:在空间联系紧密的现实中,第二产业水平对城市化发展的推动比普通回归模型所估计的要大,而第三产业水平对城市化发展的影响则比普通回归模型所估计的要小。通过两类模型的估计,我们发现,普通回归模型是一种建立在独立观测值假定基础上的理论,没有将空间相关性包括进来,使得模型的估计结果存在着一些无法避免的缺陷。而空间回归模型充分考虑了空间相关性对省域城市化的影响,并在此基础上进一步分析了城市化与经济结构之间的关系,使得到的结果更加稳健与合理。
五、结论与启示
为了考察中国内地31个省域城市化发展与经济结构变迁之间的关系,本文采用了探索性空间数据分析(ESDA)技术,首先对1978-2011年间各省域的城市化水平进行了空间自相关分析,发现省域城市化水平存在着显著的全局自相关和局部自相关,高值集聚的省域分布在东部地区(长三角、环渤海经济圈),低值集聚的省域主要分布在西部地区。进一步地,本文通过OLS回归模型,分析城市化与经济结构之间的关系,发现方程残差具有空间相关性,因此,选用了空间常系数回归模型,把相邻省域在城市化上的空间效应纳入到分析之中。实证结果表明:1978-2011年间,第二产业水平对城市化发展的影响为正,但影响程度(弹性)趋于减小,这说明中国各省域城市化发展受第二产业水平的推动明显,随着第二产业比重下降态势的显现,这种影响有减弱的趋势。第三产业水平对城市化发展的影响亦为正,且影响程度不断上升,这也表明中国各省域城市化发展受第三产业水平的影响显著,且随着第三产业比重的上升而增加。另外,需要指出的是,普通回归模型低估了第二产业对城市化的推动作用,高估了第三产业对城市化的带动作用。
由此,我们得到的启示是:1978-2011年间,中国的经济结构出现了显著的变化,第二产业比重稳中有降,第三产业比重持续上升,且第三产业对城市化发展的影响已经超过了第二产业;但是,对于中国这样的制造业大国,第二产业对城市化发展的推动作用仍然不容小觑,而第三产业(虽包含有现代服务业)对城市化发展的带动作用也不应被高估。特别是随着中国经济逐步进入“结构性减速”时期,在许多东部沿海省域,由于劳动力从生产率较高的第二产业向生产率较低的第三产业转移,已经出现了全社会劳动生产率增速下降的趋势;在中、西部地区,虽然第二产业仍然保持较高的劳动生产率增速,但多为低端制造业,当劳动力“廉价时代”趋于终结时,较高的劳动生产率增速也将难以维系。*吕健:《产业结构调整、结构性减速与经济增长分化》,《中国工业经济》,2012年第9期,第31-43页。因此,需要加快实现产业结构现代化,提高全社会劳动生产率的增速,以推动城市化又好又快地发展。具体地说,东部地区要加快发展高端制造业和现代服务业。长期以来,东部地区在生产总值、社会固定资产投资、外商投资、研究与实验发展等方面占全国的比重均大大高于其土地、人口资源占全国的比重,完全可以凭借其密集的生产力布局、较高的人力资源素质和科技创新能力,发展高端制造业,进一步保持对城市化发展的强大推动力。在服务业方面,近十年来,全球服务业的增加值之所以能够超过制造业,主要源于服务业内处于价值链高端的现代服务业的发展。而中国第三产业水平不高,无法有效地推动城市化的发展,恰恰就是因为现代服务业发展水平较低。因此,东部地区有必要通过进一步的结构调整来克服现代服务业的发展瓶颈,推动第三产业整体的升级和发展,为城市化发展提供新的动力。另外,由于西部地区承接了东部地区的产业转移,再加之“人口红利”尚存,第二产业依然具有较高的生产率增速。但是,随着产业升级、结构调整以及“人口红利”消失,西部地区也将进入“结构性减速”时代,那时的第二产业和第三产业将难以有效地推动城市化发展。因此,中、西部地区也应充分重视产业结构现代化,提前应对未来可能出现的不利影响,保证城市化在产业结构优化中不断发展。
